|
ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ПРОЦЕССА ВЫТЕСНЕНИЯ ПРИ СОПРЯЖЕНИИ РАЗЛИЧНЫХ
МОДЕЛЕЙ ФИЛЬТРАЦИИ ДВУХФАЗНОЙ ЖИДКОСТИ
О.Б. Бочаров - г. Новосибирск
И.Г. Телегин - г. Горно-Алтайск
В работе численно исследуется задача
сопряжения двух наиболее распространенных в нефтедобыче моделей
фильтрации двухфазной жидкости. В обводненной части нефтяного пласта,
где подвижная нефть почти вытеснена, капиллярные силы оказывают
слабое воздействие на процесс фильтрации двухфазной жидкости и в
этой области целесообразно использовать модель Баклея-Леверетта
(БЛ модель) с общим давлением для обеих фаз. В мало обводненной
части нефтяного пласта роль капиллярных сил при вытеснении нефти
водой оказывается весьма существенной, что приводит к необходимости
использования более сложной модели Маскета-Леверетта (МЛ модель)
с различными фазовыми давлениями. Однако, как отмечено в книге Коновалова
А.Н. [1], за счет обращения в ноль функций относительных фазовых
проницаемостей естественные граничные условия для этой модели являются
плохо обусловленными (градиенты решения в окрестности границы становятся
бесконечно большими). В работе Бочарова О.Б. [2] было предложено
в качестве граничного условия на эксплутационной скважине рассмотреть
уравнение модели Баклея-Леверетта (БЛ модель). В работе Монахова
В.Н. [3] БЛ модель предложено применять в окрестности эксплуатационной
скважины. В итоге возникает задача сопряжения МЛ и БЛ моделей. В
работе анализируется влияние сопряжения на гидродинамические характеристики
процесса вытеснения нефти водой в изотермических условиях.
1. Уравнения моделей.
Одномерная МЛ модель фильтрации двухфазной жидкости в однородной
изотропной пористой среде в отсутствии массовых сил при заданном
суммарном расходе фаз имеет вид [4]:
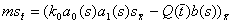
|
(1) |
где 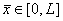 - пространственная координата, L - расстояние от нагнетательной
скважины до эксплуaтационной,
- пространственная координата, L - расстояние от нагнетательной
скважины до эксплуaтационной, 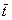 - время,
- время, 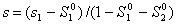 - динамическая насыщенность
смачивающей фазы, s1 - истинная насыщенность смачивающей
фазы, - динамическая насыщенность
смачивающей фазы, s1 - истинная насыщенность смачивающей
фазы, 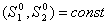 - остаточные водо-
и нефтенасыщенности, - остаточные водо-
и нефтенасыщенности, 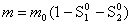 , , 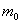 - пористость коллектора,
- пористость коллектора, 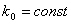 - абсолютная проницаемость коллектора;
- абсолютная проницаемость коллектора; 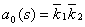 , ,
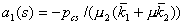 , , 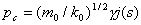 - капиллярное давление,
- капиллярное давление, 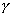 -
коэффициент поверхностного натяжения, -
коэффициент поверхностного натяжения, 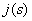 - функция Леверетта,
- функция Леверетта, 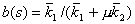 - коэффициент
подвижности вытесняющей фазы, - коэффициент
подвижности вытесняющей фазы, 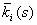 - относительные фазовые проницаемости,
- относительные фазовые проницаемости, 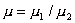
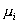 - вязкости
фаз (индекс i = 1 соответствует воде, i = 2 - нефти), - вязкости
фаз (индекс i = 1 соответствует воде, i = 2 - нефти),
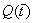 - расход
воды на нагнетательной скважине. - расход
воды на нагнетательной скважине.
При этом функциональные параметры модели имеют следующие
свойства [4]:
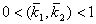 при при
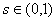 , ,
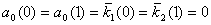 ; ;
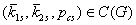 , где , где
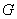 - замкнутая область в
пространстве переменных - замкнутая область в
пространстве переменных 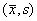 ,
причем ,
причем 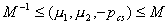 , M > 0; , M > 0;
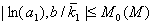 . .
К особенностям уравнения (1) следует отнести:
- вырождение типа при s = 0, s = 1,
- относительно малый коэффициент при
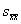 обуславливает появление
внутренних пограничных слоев (областей больших градиентов насыщенности). обуславливает появление
внутренних пограничных слоев (областей больших градиентов насыщенности).
Полагая 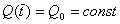 ,
введем безразмерные переменные: ,
введем безразмерные переменные:
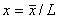
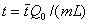 , при этом уравнение (1)
запишется в виде: , при этом уравнение (1)
запишется в виде:
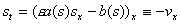
|
(2), |
где 
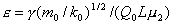 - капиллярное число, - капиллярное число,
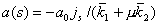 , ,
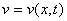 - скорость фильтрации
вытесняющей фазы. - скорость фильтрации
вытесняющей фазы.
Значению параметра 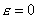 соответствует модель Баклея-Леверетта (БЛ). Обозначим через соответствует модель Баклея-Леверетта (БЛ). Обозначим через
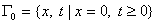 нагнетательную скважину, нагнетательную скважину,
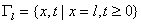 - линию сопряжения моделей, - линию сопряжения моделей,
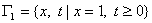 - эксплуатационную скважину,
а через - эксплуатационную скважину,
а через 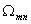 область область
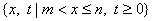 , ,
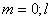 , ,
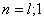 . .
2. Сопряжение МЛ и БЛ моделей с использованием смены
эволюционной переменной.
Пусть вблизи эксплутационной скважины капиллярные силы малы.
Разобьем область 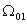 на две. В
области на две. В
области 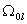 фильтрация двухфазной
жидкости описывается МЛ моделью и соответственно этому в (2) фильтрация двухфазной
жидкости описывается МЛ моделью и соответственно этому в (2)
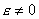 а в области а в области
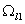 - БЛ моделью и в (2) - БЛ моделью и в (2)
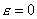 .
В области .
В области 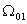 для решения
уравнения (2) предлагается изучать следующую начально-краевую задачу: для решения
уравнения (2) предлагается изучать следующую начально-краевую задачу:
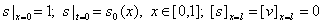
|
(3), |
где 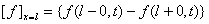 - скачок функции f (x, t) на линии
- скачок функции f (x, t) на линии
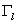 . Из условий склейки на . Из условий склейки на
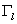 следует условие следует условие
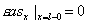 и задача (2), (3) распадается
на две подзадачи. В области и задача (2), (3) распадается
на две подзадачи. В области 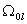
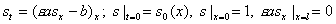
|
(4), |
В области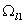 фильтрация
описывается БЛ моделью и в соответствии с этим фильтрация
описывается БЛ моделью и в соответствии с этим
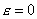 : :
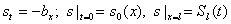
|
(5), |
В работах [3] и [5] было предложено сменить эволюционную
переменную в области 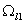 и искомую
насыщенность s на расход v. В этой ситуации легче обосновать
непрерывность расхода. Тогда задача (5) принимает вид: и искомую
насыщенность s на расход v. В этой ситуации легче обосновать
непрерывность расхода. Тогда задача (5) принимает вид:
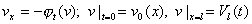
|
(6), |
где 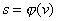 - функция,
обратная к зависимости - функция,
обратная к зависимости 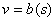 , ,
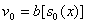 , ,
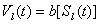 , функция , функция
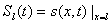 определяется по решению
определяется по решению
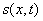 задачи (4). задачи (4).
Особенность задач (4), (6) заключается в склейке решений
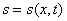
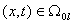 уравнения (4), эволюционного
по переменной t и функции уравнения (4), эволюционного
по переменной t и функции
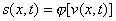
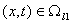 ,
выражающейся через решения ,
выражающейся через решения 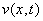 уравнения (6), эволюционного по переменной
уравнения (6), эволюционного по переменной
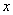
Вопросам существования обобщенного решения задачи сопряжения
МЛ и БЛ моделей (4), (6) посвящена работа [3], а первые предварительные расчеты
были проведены в [5], необходимо отметить также, что в [3] и [5] изучалась
параболически регуляризованная задача для уравнения (6).
Построение алгоритмов численного решения задачи (4), (6)
затрудненно несколькими обстоятельствами:
- Смена эволюционной переменной;
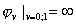 , что
затрудняет применение градиентных итерационных методов при линеаризации
разностного уравнения. , что
затрудняет применение градиентных итерационных методов при линеаризации
разностного уравнения.
Перейдем к описанию алгоритма решения задачи сопряжения (4),
(6). Вначале произведем регуляризацию используемой в дальнейшем функции
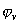 . Значение . Значение
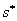 подбиралось по результатам
численных экспериментов, черта над подбиралось по результатам
численных экспериментов, черта над 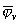 в дальнейшем изложении опускается. в дальнейшем изложении опускается.
3. Разностные схемы.
Введем основную сетку в области
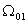 с рапределенными узлами с рапределенными узлами
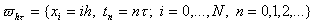 , h - шаг по
пространственной координате, , h - шаг по
пространственной координате, 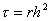 - шаг по временной переменной. Пусть при этом линии
- шаг по временной переменной. Пусть при этом линии
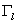 соответствует номер соответствует номер
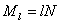 узла на сетке (предполагается,
что узла на сетке (предполагается,
что 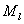 не является дробным
числом). не является дробным
числом).
Также введем вспомогательную сетку в области
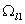
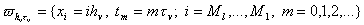 , ,
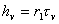 - шаг по координате - шаг по координате
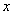 , ,
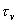 - шаг по времени. - шаг по времени.
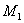 соответствует линии соответствует линии
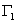 или эксплутационной скважине. или эксплутационной скважине.
При этом 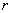 и
и 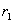 выбирались так, чтобы на
линии выбирались так, чтобы на
линии 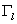 узлы сетки узлы сетки
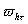 совпали с узлами сетки
совпали с узлами сетки 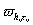 . .
Для нахождения численного решения использовались
противопотоковые схемы из соображений необходимости вычислять
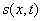 на линии склейки без
привлечения дополнительных узлов сетки. В дальнейшем используются обозначения,
принятые в [6]. на линии склейки без
привлечения дополнительных узлов сетки. В дальнейшем используются обозначения,
принятые в [6].
Уравнение МЛ модели в 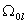 аппроксимировалось с помощью неявной разностной схемы первого
порядка: аппроксимировалось с помощью неявной разностной схемы первого
порядка:
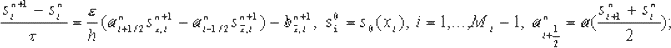
|
(7), |
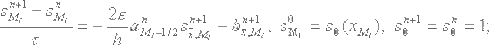
Для численного решения уравнения (5) использовалась следующая
разностная схема
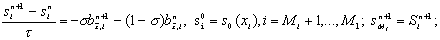
|
(8), |
где
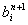 линеаризовывались как линеаризовывались как
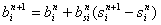 . Схема (8) при . Схема (8) при
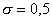 имеет погрешность
аппроксимации имеет погрешность
аппроксимации 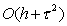 , при других
значениях , при других
значениях 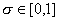
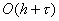
Для численного решения систем (7), (8) применялся метод
правой прогонки.
Уравнение (6) аппроксимировалось разностной схемой
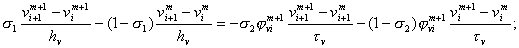
|
(9), |
где 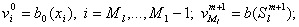
Схема (9) при 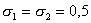 имеет погрешность аппроксимации
имеет погрешность аппроксимации 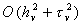 ,
при ,
при 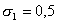 и и
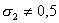 погрешность аппроксимации погрешность аппроксимации
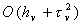 , при , при
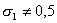 и и
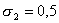
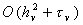 , в остальных случаях , в остальных случаях
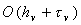 . .
На тех временных слоях, где узлы сетки
 совпадали с узлами сетки совпадали с узлами сетки
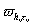 , вычисляли основные
характеристики процесса вытеснения: положение , вычисляли основные
характеристики процесса вытеснения: положение
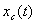 - фронтовой водонасыщенности
в БЛ модели - фронтовой водонасыщенности
в БЛ модели 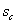 , которая
определяется решением нелинейного уравнения , которая
определяется решением нелинейного уравнения
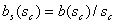
c помощью метода деления
пополам, обводненность пласта 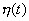 будет
будет
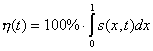
Интеграл в правой части уравнения вычислялся по формуле
трапеций. Также контролировалась
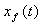 - предельная точка
распространения фронта водонасыщенности. Так как на нагнетательной скважине
задан расход, а жидкости считаются несжимаемыми, то контроль решения
осуществлялся прежде всего по водному балансу. - предельная точка
распространения фронта водонасыщенности. Так как на нагнетательной скважине
задан расход, а жидкости считаются несжимаемыми, то контроль решения
осуществлялся прежде всего по водному балансу.
В численных расчетах использовался следующий модельный набор
параметров:
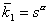
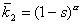 ; ;
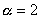 ; ;
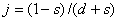 ; ;
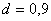 ; ;
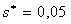 ; ;
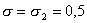 . .
Выбор 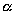 был обусловлен простотой вычисления обратной функции
был обусловлен простотой вычисления обратной функции
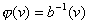 для уравнения (6). для уравнения (6).
Ниже на рисунках толстыми линиями обозначены решения или
характеристики, относящиеся к задачам сопряжения, а тонкими - результаты
контрольного счета во всей области 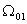 ,
пунктир - линия ,
пунктир - линия 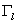 . .
4. Результаты расчетов.
В численных расчетах использовались шаги сетки
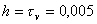 , ,
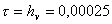 , (N = 200). , (N = 200).
a) Расчеты при разных
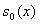 . .
Первоначально тестировали разностную схему (9) на
аппроксимацию при малых 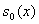 .
Для этого во всей области решали задачу для БЛ модели по схеме (8) без линии
сопряжения и по схемам (8), (9) с линией сопряжения. При этом
l бралось равным 0,8, .
Для этого во всей области решали задачу для БЛ модели по схеме (8) без линии
сопряжения и по схемам (8), (9) с линией сопряжения. При этом
l бралось равным 0,8, 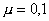 . .
Сравнение численного решения задачи (4), (6) с решением по БЛ
модели во всей области показывает, что дисбаланс при
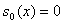 составляет 1,9-2,3%, а при составляет 1,9-2,3%, а при
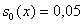 порядка 0,5-0,7%. При порядка 0,5-0,7%. При
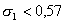 и и
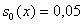 имели место осцилляции за
фронтом водонасыщенности, при этом ухудшался баланс. С уменьшением имели место осцилляции за
фронтом водонасыщенности, при этом ухудшался баланс. С уменьшением
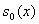 осцилляции появляются даже
при больших весах. Необходимо также отметить, что веса в схеме (9)
взаимосвязаны друг с другом и увеличение веса осцилляции появляются даже
при больших весах. Необходимо также отметить, что веса в схеме (9)
взаимосвязаны друг с другом и увеличение веса
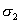 приводило к уменьшению
осцилляционных эффектов. Имело место опережающее движение фронта при малых приводило к уменьшению
осцилляционных эффектов. Имело место опережающее движение фронта при малых
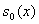 по модели сопряжения.
Наилучший результат получился при по модели сопряжения.
Наилучший результат получился при
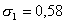 , ,
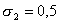 , ,
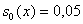 , рис. 1. В дальнейшем будет
предполагаться, если не оговорено дополнительно, что схема (9) используется
именно с этими параметрами. , рис. 1. В дальнейшем будет
предполагаться, если не оговорено дополнительно, что схема (9) используется
именно с этими параметрами.
b) Особенности решений задачи сопряжения (4), (6).
Характерной особенностью решения задачи сопряжения является
подъем и выполаживание графика в точке
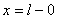 ,
обуславливаемое наличием в этой точке краевого условия ,
обуславливаемое наличием в этой точке краевого условия
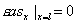 , (рис. 2), при этом , (рис. 2), при этом
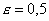 , ,
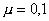 . Второй особенностью решений
задачи сопряжения является эффект недобегания, который выражается в том, что в . Второй особенностью решений
задачи сопряжения является эффект недобегания, который выражается в том, что в
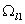 формируется скачкообразный
профиль водонасыщенности и поэтому прорыва воды дисбаланс обводненностей между
моделями составил 6,1%. приход воды в задаче сопряжения на эксплутационную
скважину происходит позднее, чем в задаче для МЛ модели во всей области.
Следствием эффектов недобегания и выполаживания является тот факт, что после
момента прихода воды на эксплутационную скважину расчитанного по МЛ модели
обводненность пласта формируется скачкообразный
профиль водонасыщенности и поэтому прорыва воды дисбаланс обводненностей между
моделями составил 6,1%. приход воды в задаче сопряжения на эксплутационную
скважину происходит позднее, чем в задаче для МЛ модели во всей области.
Следствием эффектов недобегания и выполаживания является тот факт, что после
момента прихода воды на эксплутационную скважину расчитанного по МЛ модели
обводненность пласта 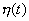 в задаче
сопряжения выше. На рис. 3 приведены графики решений задачи (4), (6) и решений
по МЛ модели в случае капиллярного запирания. В этом случае после в задаче
сопряжения выше. На рис. 3 приведены графики решений задачи (4), (6) и решений
по МЛ модели в случае капиллярного запирания. В этом случае после
 |
 |
| рис. 1 | рис. 2 |
c) Эволюция продвижения фронтов 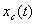 и и 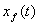 . .
Анализ движения фронтовой водонасыщенности (в условиях,
соответствующих рис. 2) показывает, что график
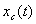 для модели сопряжения состоит из трех участков (рис. 4). На первом участке он
совпадает с графиком
для модели сопряжения состоит из трех участков (рис. 4). На первом участке он
совпадает с графиком 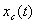 для МЛ модели в
для МЛ модели в 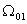 . Второй
участок характеризуется ускорением продвижения . Второй
участок характеризуется ускорением продвижения
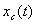 (он догоняет (он догоняет
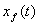 ).
Это объясняется тем, что в течение некоторого времени формируется резкий
(скачкообразный) профиль водонасыщенности, характерный для БЛ модели. При этом
происходит торможение ).
Это объясняется тем, что в течение некоторого времени формируется резкий
(скачкообразный) профиль водонасыщенности, характерный для БЛ модели. При этом
происходит торможение 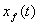 , так как
перестают работать капиллярные силы. На третьем участке происходит
характерное для БЛ модели равномерное движение , так как
перестают работать капиллярные силы. На третьем участке происходит
характерное для БЛ модели равномерное движение
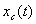 . .
График функции 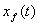 в задаче сопряжения в отличии от графика для МЛ модели, состоит из двух
участков, которые соответствуют наличию капиллярных сил и их отсутствию.
в задаче сопряжения в отличии от графика для МЛ модели, состоит из двух
участков, которые соответствуют наличию капиллярных сил и их отсутствию.
 |
 |
| рис. 3 | рис. 4 |
d) Влияние размеров прискважинной зоны.
- при
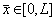 дисбаланс по обводненности между решениями при времени t = 1 составил
0,05%, а максимальный дисбаланс был равен 0,09%. Очевидно, что при таком
дисбаланс по обводненности между решениями при времени t = 1 составил
0,05%, а максимальный дисбаланс был равен 0,09%. Очевидно, что при таком
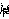 различия в гидродинамических
характеристиках незначительны и проявляются только в модуле градиента
водонасыщенности на эксплутационной скважине. различия в гидродинамических
характеристиках незначительны и проявляются только в модуле градиента
водонасыщенности на эксплутационной скважине.
- при l = 0,95 дисбаланс по обводненности между
решениями при t = 1 составил 0,26%, а максимальный дисбаланс был равен
0,43%.
- при l = 0,9 дисбаланс по обводненности между
решениями при t = 1 составил 0,54%, а максимальный дисбаланс был равен
0,87%.
- при l = 0,8 дисбаланс по обводненности между
решениями при t = 1 составил 1,13%, а максимальный дисбаланс был равен
1,78%.
Разница между решениями в норме
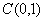 при малых при малых
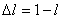 (
(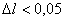 ) до момента прихода воды на
эксплутационную скважину по модели сопряжения была меньше 0,01, а при ) до момента прихода воды на
эксплутационную скважину по модели сопряжения была меньше 0,01, а при
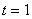 была порядка 0,001. При
больших была порядка 0,001. При
больших 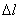 до прихода воды
разница между решениями имела порядок 0,1, а при до прихода воды
разница между решениями имела порядок 0,1, а при
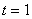 не превышала 0,03. не превышала 0,03.
С увеличением 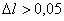 Эффекты недобегания и выполаживания в окрестности
Эффекты недобегания и выполаживания в окрестности
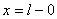 усиливаются, а в области усиливаются, а в области
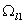 начинает формироваться
характерный для БЛ модели скачкообразный профиль водонасыщенности. начинает формироваться
характерный для БЛ модели скачкообразный профиль водонасыщенности.
Интересным является тот факт, что точка перегиба фронта (или
фронтовая водонасыщенность, в дальнейшем 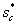 ) у этого фронта оказывается меньше, чем фронтовая водонасыщенность ) у этого фронта оказывается меньше, чем фронтовая водонасыщенность
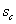
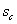 при выше используемых
параметрах была равна 0,3015, в то же время, как видно из рис. 2, при выше используемых
параметрах была равна 0,3015, в то же время, как видно из рис. 2,
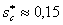 в области в области
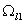 .
При уменьшении .
При уменьшении 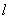 увеличивается
зона БЛ модели и увеличивается
зона БЛ модели и 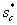 при прохождении
при прохождении 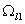 растет до
растет до 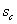 Так при
Так при 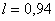
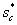 равно равно
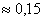 , а при , а при
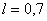 вырастает уже до вырастает уже до
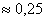 . Это явление объясняется тем,
что на левом конце для БЛ модели граничное условие . Это явление объясняется тем,
что на левом конце для БЛ модели граничное условие
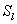 в начальные моменты времени
меньше в начальные моменты времени
меньше 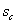 . Данный эффект
проявляется в том, что приход воды на эксплутационную скважину осуществляется
с различными . Данный эффект
проявляется в том, что приход воды на эксплутационную скважину осуществляется
с различными 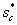 ,
зависящими от ,
зависящими от 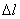 , на котором
происходит поднятие , на котором
происходит поднятие 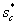 . .
e) Влияние капиллярного числа 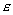 . .
В задаче сопряжения МЛ и БЛ моделей
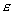 оказывает влияние на область оказывает влияние на область
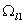 неявно. С увеличением неявно. С увеличением
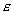 эффект выполаживания
усиливается, но в то же время увеличивается гладкость функции эффект выполаживания
усиливается, но в то же время увеличивается гладкость функции
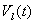 ,
что влияет на процесс формирования начального профиля водонасыщенности в зоне
действия БЛ модели. С уменьшением ,
что влияет на процесс формирования начального профиля водонасыщенности в зоне
действия БЛ модели. С уменьшением 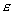 отличия в решениях уменьшаются. Так при отличия в решениях уменьшаются. Так при
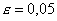 и и
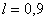 различия в решениях по задаче сопряжения и по МЛ модели во всей области не
превышали 0,01 в норме
различия в решениях по задаче сопряжения и по МЛ модели во всей области не
превышали 0,01 в норме 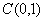 Отметим, что в пластовых условиях обычно
Отметим, что в пластовых условиях обычно
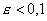 . .
f) Расчеты при разных 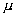 . .
Известно, что уменьшение
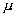 приводит к уменьшению приводит к уменьшению
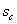 ,
что в свою очередь уменьшает время безводной нефтеотдачи. ,
что в свою очередь уменьшает время безводной нефтеотдачи.
Были проведены многовариантные расчеты с различными
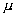 и фиксированными и фиксированными
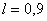 , ,
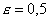 , ,
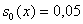 , ,
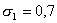 .
На рис. 5, 2, 6 приведены графики решений по задаче сопряжения МЛ и БЛ моделей и
по МЛ модели (на рис. 2). На рис. 5 приведены решения при .
На рис. 5, 2, 6 приведены графики решений по задаче сопряжения МЛ и БЛ моделей и
по МЛ модели (на рис. 2). На рис. 5 приведены решения при
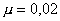 . Фронтовая водонасыщенность . Фронтовая водонасыщенность
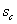 была при этом равна 0,14.
Дисбаланс обводненностей при времени была при этом равна 0,14.
Дисбаланс обводненностей при времени
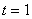 между моделями составил 1,34%.
Он же был и максимальным дисбалансом. На рис. 2 приведены решения при между моделями составил 1,34%.
Он же был и максимальным дисбалансом. На рис. 2 приведены решения при
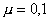 .
Фронтовая водонасыщенность .
Фронтовая водонасыщенность
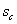 была при этом равна 0,3015,
а была при этом равна 0,3015,
а 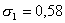 .
Дисбаланс обводненностей при времени .
Дисбаланс обводненностей при времени 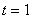 между моделями был равен 0,54%, а максимальный дисбаланс был равен
0,87%. На рис. 6 приведены решения при между моделями был равен 0,54%, а максимальный дисбаланс был равен
0,87%. На рис. 6 приведены решения при 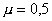 . Фронтовая водонасыщенность . Фронтовая водонасыщенность 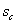 была при этом равна была при этом равна 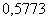 .
Дисбаланс обводненности при времени .
Дисбаланс обводненности при времени 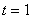 между моделями составил 0,16%, а максимальный дисбаланс был равен
1,42%. Таким образом, можно сделать вывод, что при больших между моделями составил 0,16%, а максимальный дисбаланс был равен
1,42%. Таким образом, можно сделать вывод, что при больших
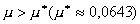 дисбаланс и различие между
решениями в норме дисбаланс и различие между
решениями в норме 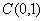 с течением
времени быстро уменьшается, это хорошо видно на рис. 7, где изображены графики
обводненностей, соответствующие рис. 6. с течением
времени быстро уменьшается, это хорошо видно на рис. 7, где изображены графики
обводненностей, соответствующие рис. 6.
Для того, чтобы выяснить, как ведет себя функция дисбаланса
при малых 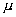 , были проведены
расчеты с разными , были проведены
расчеты с разными 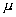 . Было
установлено, что дисбаланс растет до определенного момента . Было
установлено, что дисбаланс растет до определенного момента
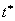 , а далее происходит уменьшение
дисбаланса и разницы между решениями в норме , а далее происходит уменьшение
дисбаланса и разницы между решениями в норме
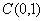 . При выше описанных параметрах
и . При выше описанных параметрах
и 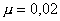
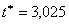
 |
 |
| рис. 5 | рис. 6 |
 |
 |
| рис. 7 | рис. 8 |
Видно, что 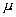 оказывает сложное воздействие на решение задачи сопряжения. При уменьшении
оказывает сложное воздействие на решение задачи сопряжения. При уменьшении
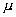 происходит увеличение отрезка
подъема графика водонасыщенности в области происходит увеличение отрезка
подъема графика водонасыщенности в области
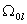 над графиком водонасыщенности
по МЛ модели на всей области над графиком водонасыщенности
по МЛ модели на всей области 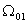 .
Уменьшение .
Уменьшение 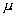 приводит также и к
возрастанию градиента водонасыщенности вблизи эксплутационной скважины после
прорыва воды по модели сопряжения. Из рис. 8, на котором изображены графики приводит также и к
возрастанию градиента водонасыщенности вблизи эксплутационной скважины после
прорыва воды по модели сопряжения. Из рис. 8, на котором изображены графики
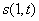 , соответствующие рис. 6,
видно, что график функции , соответствующие рис. 6,
видно, что график функции 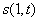 будет
иметь сложную структуру, зависящую от будет
иметь сложную структуру, зависящую от 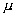 . Этот график состоит из трех основных участков. На первом участке . Этот график состоит из трех основных участков. На первом участке
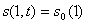 . Вследствии эффекта
недобегания этот участок в задаче сопряжения (4), (6), как правило, будет
больше соответствующего участка в МЛ модели на всей области . Вследствии эффекта
недобегания этот участок в задаче сопряжения (4), (6), как правило, будет
больше соответствующего участка в МЛ модели на всей области
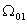 . На втором участке,
вследствии эффектов недобегания и выполаживания, прорыв воды в эксплутационную
скважину происходит по модели сопряжения с большим модулем градиента
водонасыщенности. При больших . На втором участке,
вследствии эффектов недобегания и выполаживания, прорыв воды в эксплутационную
скважину происходит по модели сопряжения с большим модулем градиента
водонасыщенности. При больших 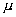 водонасыщенность на линии
водонасыщенность на линии 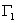 по модели сопряжения на втором участке будет больше соответствующего по МЛ
модели (при малых -
по модели сопряжения на втором участке будет больше соответствующего по МЛ
модели (при малых - 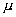 меньше).
На третьем - происходит сближение профилей меньше).
На третьем - происходит сближение профилей 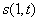 . .
Эксперименты показали, что при малых
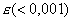 , ,
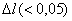 и больших и больших
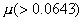 гораздо удобнее и экомичнее вместо модели сопряжения использовать МЛ модель.
В тоже время при больших
гораздо удобнее и экомичнее вместо модели сопряжения использовать МЛ модель.
В тоже время при больших 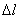 , ,
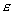 и малых и малых
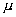 необходимо для получения более точных численных результатов применять модель
сопряжения (4), (6).
необходимо для получения более точных численных результатов применять модель
сопряжения (4), (6).
Литература
- Коновалов А.Н. Задачи фильтрации многофазной несжимаемой
жидкости. Новосибирск, СО Наука, 1988, 166 с.
- Бочаров О.Б. О задаче с сосредоточенной емкостью для
одномерных уравнений двухфазной фильтрации. Сб.н.тр. Механика быстропротекающих
процессов (Динамика сплошной среды), ИГиЛ СО РАН, 1985, вып. 73, с. 149-155.
- Монахов В.Н. Сопряжение основных математических моделей
фильтрации двухфазной жидкости. Математическое моделирование, 2002 (в печати).
- Антонцев С.Н., Кажихов А.В., Монахов В.Н. Краевые задачи
механики неоднородных жидкостей. Новосибирск, СО Наука, 1983, 316 с.
- Телегин И.Г. Численная реализация сопряжения основных
моделей фильтрации двухфазной жидкости. Сб.н.тр. Динамика сплошной среды,
ИГиЛ СО РАН, 2000, вып. 116, с. 107-111.
- Самарский А.А. Введение в теорию разностных схем. М.,
Наука, 1971.
|




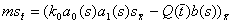
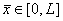 - пространственная координата, L - расстояние от нагнетательной
скважины до эксплуaтационной,
- пространственная координата, L - расстояние от нагнетательной
скважины до эксплуaтационной, 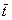 - время,
- время, 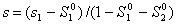 - динамическая насыщенность
смачивающей фазы, s1 - истинная насыщенность смачивающей
фазы,
- динамическая насыщенность
смачивающей фазы, s1 - истинная насыщенность смачивающей
фазы, 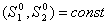 - остаточные водо-
и нефтенасыщенности,
- остаточные водо-
и нефтенасыщенности, 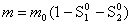 ,
, 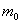 - пористость коллектора,
- пористость коллектора, 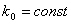 - абсолютная проницаемость коллектора;
- абсолютная проницаемость коллектора; 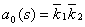 ,
,
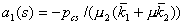 ,
, 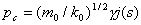 - капиллярное давление,
- капиллярное давление, 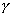 -
коэффициент поверхностного натяжения,
-
коэффициент поверхностного натяжения, 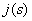 - функция Леверетта,
- функция Леверетта, 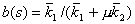 - коэффициент
подвижности вытесняющей фазы,
- коэффициент
подвижности вытесняющей фазы, 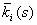 - относительные фазовые проницаемости,
- относительные фазовые проницаемости, 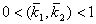 при
при
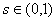 ,
,
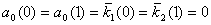 ;
;
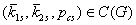 , где
, где
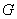 - замкнутая область в
пространстве переменных
- замкнутая область в
пространстве переменных 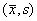 ,
причем
,
причем 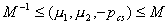 , M > 0;
, M > 0;
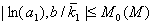 .
.
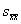 обуславливает появление
внутренних пограничных слоев (областей больших градиентов насыщенности).
обуславливает появление
внутренних пограничных слоев (областей больших градиентов насыщенности).
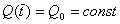 ,
введем безразмерные переменные:
,
введем безразмерные переменные:
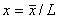
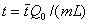 , при этом уравнение (1)
запишется в виде:
, при этом уравнение (1)
запишется в виде:
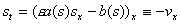

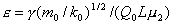 - капиллярное число,
- капиллярное число,
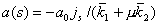 ,
,
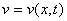 - скорость фильтрации
вытесняющей фазы.
- скорость фильтрации
вытесняющей фазы.
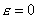 соответствует модель Баклея-Леверетта (БЛ). Обозначим через
соответствует модель Баклея-Леверетта (БЛ). Обозначим через
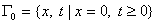 нагнетательную скважину,
нагнетательную скважину,
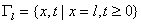 - линию сопряжения моделей,
- линию сопряжения моделей,
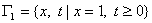 - эксплуатационную скважину,
а через
- эксплуатационную скважину,
а через 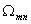 область
область
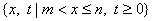 ,
,
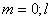 ,
,
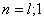 .
.
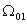 на две. В
области
на две. В
области 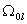 фильтрация двухфазной
жидкости описывается МЛ моделью и соответственно этому в (2)
фильтрация двухфазной
жидкости описывается МЛ моделью и соответственно этому в (2)
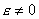 а в области
а в области
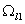 - БЛ моделью и в (2)
- БЛ моделью и в (2)
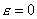 .
В области
.
В области 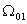 для решения
уравнения (2) предлагается изучать следующую начально-краевую задачу:
для решения
уравнения (2) предлагается изучать следующую начально-краевую задачу:
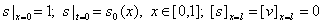
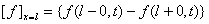 - скачок функции f (x, t) на линии
- скачок функции f (x, t) на линии
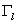 . Из условий склейки на
. Из условий склейки на
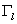 следует условие
следует условие
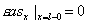 и задача (2), (3) распадается
на две подзадачи. В области
и задача (2), (3) распадается
на две подзадачи. В области 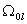
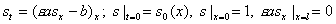
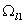 фильтрация
описывается БЛ моделью и в соответствии с этим
фильтрация
описывается БЛ моделью и в соответствии с этим
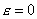 :
:
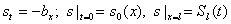
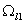 и искомую
насыщенность s на расход v. В этой ситуации легче обосновать
непрерывность расхода. Тогда задача (5) принимает вид:
и искомую
насыщенность s на расход v. В этой ситуации легче обосновать
непрерывность расхода. Тогда задача (5) принимает вид:
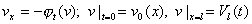
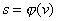 - функция,
обратная к зависимости
- функция,
обратная к зависимости 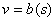 ,
,
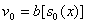 ,
,
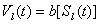 , функция
, функция
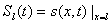 определяется по решению
определяется по решению
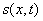 задачи (4).
задачи (4).
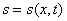
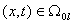 уравнения (4), эволюционного
по переменной t и функции
уравнения (4), эволюционного
по переменной t и функции
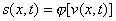
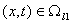 ,
выражающейся через решения
,
выражающейся через решения 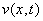 уравнения (6), эволюционного по переменной
уравнения (6), эволюционного по переменной
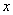
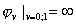 , что
затрудняет применение градиентных итерационных методов при линеаризации
разностного уравнения.
, что
затрудняет применение градиентных итерационных методов при линеаризации
разностного уравнения.
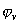 . Значение
. Значение
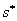 подбиралось по результатам
численных экспериментов, черта над
подбиралось по результатам
численных экспериментов, черта над 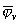 в дальнейшем изложении опускается.
в дальнейшем изложении опускается.
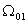 с рапределенными узлами
с рапределенными узлами
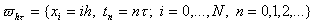 , h - шаг по
пространственной координате,
, h - шаг по
пространственной координате, 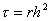 - шаг по временной переменной. Пусть при этом линии
- шаг по временной переменной. Пусть при этом линии
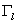 соответствует номер
соответствует номер
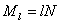 узла на сетке (предполагается,
что
узла на сетке (предполагается,
что 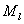 не является дробным
числом).
не является дробным
числом).
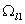
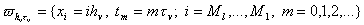 ,
,
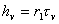 - шаг по координате
- шаг по координате
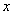 ,
,
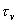 - шаг по времени.
- шаг по времени.
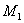 соответствует линии
соответствует линии
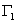 или эксплутационной скважине.
или эксплутационной скважине.
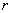 и
и 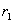 выбирались так, чтобы на
линии
выбирались так, чтобы на
линии 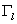 узлы сетки
узлы сетки
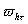 совпали с узлами сетки
совпали с узлами сетки 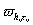 .
.
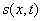 на линии склейки без
привлечения дополнительных узлов сетки. В дальнейшем используются обозначения,
принятые в [6].
на линии склейки без
привлечения дополнительных узлов сетки. В дальнейшем используются обозначения,
принятые в [6].
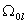 аппроксимировалось с помощью неявной разностной схемы первого
порядка:
аппроксимировалось с помощью неявной разностной схемы первого
порядка:
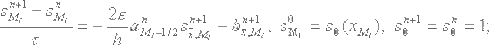
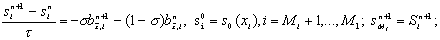
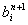 линеаризовывались как
линеаризовывались как
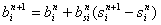 . Схема (8) при
. Схема (8) при
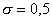 имеет погрешность
аппроксимации
имеет погрешность
аппроксимации 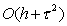 , при других
значениях
, при других
значениях 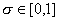
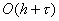
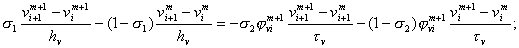
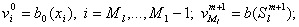
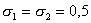 имеет погрешность аппроксимации
имеет погрешность аппроксимации 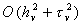 ,
при
,
при 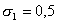 и
и
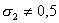 погрешность аппроксимации
погрешность аппроксимации
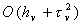 , при
, при
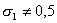 и
и
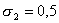
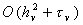 , в остальных случаях
, в остальных случаях
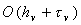 .
.
 совпадали с узлами сетки
совпадали с узлами сетки
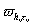 , вычисляли основные
характеристики процесса вытеснения: положение
, вычисляли основные
характеристики процесса вытеснения: положение
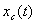 - фронтовой водонасыщенности
в БЛ модели
- фронтовой водонасыщенности
в БЛ модели 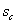 , которая
определяется решением нелинейного уравнения
, которая
определяется решением нелинейного уравнения
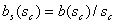
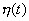 будет
будет
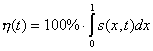
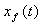 - предельная точка
распространения фронта водонасыщенности. Так как на нагнетательной скважине
задан расход, а жидкости считаются несжимаемыми, то контроль решения
осуществлялся прежде всего по водному балансу.
- предельная точка
распространения фронта водонасыщенности. Так как на нагнетательной скважине
задан расход, а жидкости считаются несжимаемыми, то контроль решения
осуществлялся прежде всего по водному балансу.
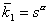
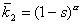 ;
;
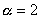 ;
;
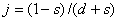 ;
;
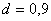 ;
;
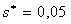 ;
;
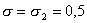 .
.
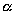 был обусловлен простотой вычисления обратной функции
был обусловлен простотой вычисления обратной функции
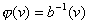 для уравнения (6).
для уравнения (6).
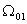 ,
пунктир - линия
,
пунктир - линия 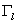 .
.
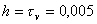 ,
,
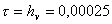 , (N = 200).
, (N = 200).
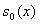 .
.
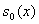 .
Для этого во всей области решали задачу для БЛ модели по схеме (8) без линии
сопряжения и по схемам (8), (9) с линией сопряжения. При этом
l бралось равным 0,8,
.
Для этого во всей области решали задачу для БЛ модели по схеме (8) без линии
сопряжения и по схемам (8), (9) с линией сопряжения. При этом
l бралось равным 0,8, 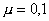 .
.
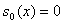 составляет 1,9-2,3%, а при
составляет 1,9-2,3%, а при
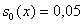 порядка 0,5-0,7%. При
порядка 0,5-0,7%. При
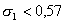 и
и
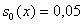 имели место осцилляции за
фронтом водонасыщенности, при этом ухудшался баланс. С уменьшением
имели место осцилляции за
фронтом водонасыщенности, при этом ухудшался баланс. С уменьшением
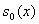 осцилляции появляются даже
при больших весах. Необходимо также отметить, что веса в схеме (9)
взаимосвязаны друг с другом и увеличение веса
осцилляции появляются даже
при больших весах. Необходимо также отметить, что веса в схеме (9)
взаимосвязаны друг с другом и увеличение веса
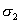 приводило к уменьшению
осцилляционных эффектов. Имело место опережающее движение фронта при малых
приводило к уменьшению
осцилляционных эффектов. Имело место опережающее движение фронта при малых
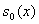 по модели сопряжения.
Наилучший результат получился при
по модели сопряжения.
Наилучший результат получился при
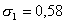 ,
,
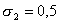 ,
,
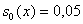 , рис. 1. В дальнейшем будет
предполагаться, если не оговорено дополнительно, что схема (9) используется
именно с этими параметрами.
, рис. 1. В дальнейшем будет
предполагаться, если не оговорено дополнительно, что схема (9) используется
именно с этими параметрами.
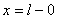 ,
обуславливаемое наличием в этой точке краевого условия
,
обуславливаемое наличием в этой точке краевого условия
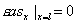 , (рис. 2), при этом
, (рис. 2), при этом
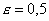 ,
,
 . Второй особенностью решений
задачи сопряжения является эффект недобегания, который выражается в том, что в
. Второй особенностью решений
задачи сопряжения является эффект недобегания, который выражается в том, что в
 формируется скачкообразный
профиль водонасыщенности и поэтому прорыва воды дисбаланс обводненностей между
моделями составил 6,1%. приход воды в задаче сопряжения на эксплутационную
скважину происходит позднее, чем в задаче для МЛ модели во всей области.
Следствием эффектов недобегания и выполаживания является тот факт, что после
момента прихода воды на эксплутационную скважину расчитанного по МЛ модели
обводненность пласта
формируется скачкообразный
профиль водонасыщенности и поэтому прорыва воды дисбаланс обводненностей между
моделями составил 6,1%. приход воды в задаче сопряжения на эксплутационную
скважину происходит позднее, чем в задаче для МЛ модели во всей области.
Следствием эффектов недобегания и выполаживания является тот факт, что после
момента прихода воды на эксплутационную скважину расчитанного по МЛ модели
обводненность пласта 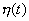 в задаче
сопряжения выше. На рис. 3 приведены графики решений задачи (4), (6) и решений
по МЛ модели в случае капиллярного запирания. В этом случае после
в задаче
сопряжения выше. На рис. 3 приведены графики решений задачи (4), (6) и решений
по МЛ модели в случае капиллярного запирания. В этом случае после


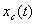 и
и 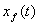 .
.
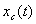 для модели сопряжения состоит из трех участков (рис. 4). На первом участке он
совпадает с графиком
для модели сопряжения состоит из трех участков (рис. 4). На первом участке он
совпадает с графиком 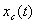 для МЛ модели в
для МЛ модели в 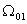 . Второй
участок характеризуется ускорением продвижения
. Второй
участок характеризуется ускорением продвижения
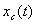 (он догоняет
(он догоняет
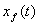 ).
Это объясняется тем, что в течение некоторого времени формируется резкий
(скачкообразный) профиль водонасыщенности, характерный для БЛ модели. При этом
происходит торможение
).
Это объясняется тем, что в течение некоторого времени формируется резкий
(скачкообразный) профиль водонасыщенности, характерный для БЛ модели. При этом
происходит торможение 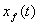 , так как
перестают работать капиллярные силы. На третьем участке происходит
характерное для БЛ модели равномерное движение
, так как
перестают работать капиллярные силы. На третьем участке происходит
характерное для БЛ модели равномерное движение
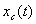 .
.
 в задаче сопряжения в отличии от графика для МЛ модели, состоит из двух
участков, которые соответствуют наличию капиллярных сил и их отсутствию.
в задаче сопряжения в отличии от графика для МЛ модели, состоит из двух
участков, которые соответствуют наличию капиллярных сил и их отсутствию.


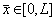 дисбаланс по обводненности между решениями при времени t = 1 составил
0,05%, а максимальный дисбаланс был равен 0,09%. Очевидно, что при таком
дисбаланс по обводненности между решениями при времени t = 1 составил
0,05%, а максимальный дисбаланс был равен 0,09%. Очевидно, что при таком
 различия в гидродинамических
характеристиках незначительны и проявляются только в модуле градиента
водонасыщенности на эксплутационной скважине.
различия в гидродинамических
характеристиках незначительны и проявляются только в модуле градиента
водонасыщенности на эксплутационной скважине.
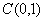 при малых
при малых
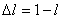 (
(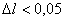 ) до момента прихода воды на
эксплутационную скважину по модели сопряжения была меньше 0,01, а при
) до момента прихода воды на
эксплутационную скважину по модели сопряжения была меньше 0,01, а при
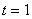 была порядка 0,001. При
больших
была порядка 0,001. При
больших 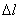 до прихода воды
разница между решениями имела порядок 0,1, а при
до прихода воды
разница между решениями имела порядок 0,1, а при
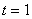 не превышала 0,03.
не превышала 0,03.
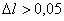 Эффекты недобегания и выполаживания в окрестности
Эффекты недобегания и выполаживания в окрестности
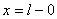 усиливаются, а в области
усиливаются, а в области
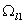 начинает формироваться
характерный для БЛ модели скачкообразный профиль водонасыщенности.
начинает формироваться
характерный для БЛ модели скачкообразный профиль водонасыщенности.
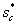 ) у этого фронта оказывается меньше, чем фронтовая водонасыщенность
) у этого фронта оказывается меньше, чем фронтовая водонасыщенность
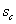
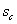 при выше используемых
параметрах была равна 0,3015, в то же время, как видно из рис. 2,
при выше используемых
параметрах была равна 0,3015, в то же время, как видно из рис. 2,
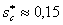 в области
в области
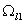 .
При уменьшении
.
При уменьшении 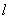 увеличивается
зона БЛ модели и
увеличивается
зона БЛ модели и 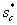 при прохождении
при прохождении 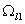 растет до
растет до 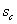 Так при
Так при 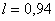
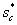 равно
равно
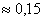 , а при
, а при
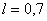 вырастает уже до
вырастает уже до
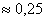 . Это явление объясняется тем,
что на левом конце для БЛ модели граничное условие
. Это явление объясняется тем,
что на левом конце для БЛ модели граничное условие
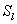 в начальные моменты времени
меньше
в начальные моменты времени
меньше 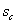 . Данный эффект
проявляется в том, что приход воды на эксплутационную скважину осуществляется
с различными
. Данный эффект
проявляется в том, что приход воды на эксплутационную скважину осуществляется
с различными 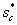 ,
зависящими от
,
зависящими от 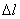 , на котором
происходит поднятие
, на котором
происходит поднятие 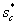 .
.
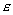 .
.
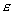 оказывает влияние на область
оказывает влияние на область
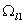 неявно. С увеличением
неявно. С увеличением
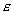 эффект выполаживания
усиливается, но в то же время увеличивается гладкость функции
эффект выполаживания
усиливается, но в то же время увеличивается гладкость функции
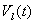 ,
что влияет на процесс формирования начального профиля водонасыщенности в зоне
действия БЛ модели. С уменьшением
,
что влияет на процесс формирования начального профиля водонасыщенности в зоне
действия БЛ модели. С уменьшением 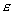 отличия в решениях уменьшаются. Так при
отличия в решениях уменьшаются. Так при
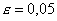 и
и
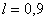 различия в решениях по задаче сопряжения и по МЛ модели во всей области не
превышали 0,01 в норме
различия в решениях по задаче сопряжения и по МЛ модели во всей области не
превышали 0,01 в норме 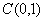 Отметим, что в пластовых условиях обычно
Отметим, что в пластовых условиях обычно
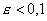 .
.
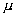 .
.
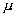 приводит к уменьшению
приводит к уменьшению
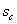 ,
что в свою очередь уменьшает время безводной нефтеотдачи.
,
что в свою очередь уменьшает время безводной нефтеотдачи.
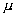 и фиксированными
и фиксированными
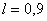 ,
,
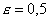 ,
,
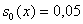 ,
,
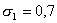 .
На рис. 5, 2, 6 приведены графики решений по задаче сопряжения МЛ и БЛ моделей и
по МЛ модели (на рис. 2). На рис. 5 приведены решения при
.
На рис. 5, 2, 6 приведены графики решений по задаче сопряжения МЛ и БЛ моделей и
по МЛ модели (на рис. 2). На рис. 5 приведены решения при
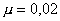 . Фронтовая водонасыщенность
. Фронтовая водонасыщенность
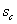 была при этом равна 0,14.
Дисбаланс обводненностей при времени
была при этом равна 0,14.
Дисбаланс обводненностей при времени
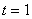 между моделями составил 1,34%.
Он же был и максимальным дисбалансом. На рис. 2 приведены решения при
между моделями составил 1,34%.
Он же был и максимальным дисбалансом. На рис. 2 приведены решения при
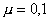 .
Фронтовая водонасыщенность
.
Фронтовая водонасыщенность
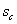 была при этом равна 0,3015,
а
была при этом равна 0,3015,
а 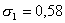 .
Дисбаланс обводненностей при времени
.
Дисбаланс обводненностей при времени 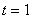 между моделями был равен 0,54%, а максимальный дисбаланс был равен
0,87%. На рис. 6 приведены решения при
между моделями был равен 0,54%, а максимальный дисбаланс был равен
0,87%. На рис. 6 приведены решения при 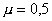 . Фронтовая водонасыщенность
. Фронтовая водонасыщенность 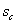 была при этом равна
была при этом равна 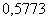 .
Дисбаланс обводненности при времени
.
Дисбаланс обводненности при времени 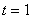 между моделями составил 0,16%, а максимальный дисбаланс был равен
1,42%. Таким образом, можно сделать вывод, что при больших
между моделями составил 0,16%, а максимальный дисбаланс был равен
1,42%. Таким образом, можно сделать вывод, что при больших
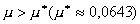 дисбаланс и различие между
решениями в норме
дисбаланс и различие между
решениями в норме 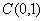 с течением
времени быстро уменьшается, это хорошо видно на рис. 7, где изображены графики
обводненностей, соответствующие рис. 6.
с течением
времени быстро уменьшается, это хорошо видно на рис. 7, где изображены графики
обводненностей, соответствующие рис. 6.
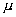 , были проведены
расчеты с разными
, были проведены
расчеты с разными 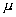 . Было
установлено, что дисбаланс растет до определенного момента
. Было
установлено, что дисбаланс растет до определенного момента
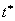 , а далее происходит уменьшение
дисбаланса и разницы между решениями в норме
, а далее происходит уменьшение
дисбаланса и разницы между решениями в норме
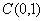 . При выше описанных параметрах
и
. При выше описанных параметрах
и 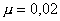
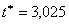




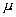 оказывает сложное воздействие на решение задачи сопряжения. При уменьшении
оказывает сложное воздействие на решение задачи сопряжения. При уменьшении
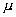 происходит увеличение отрезка
подъема графика водонасыщенности в области
происходит увеличение отрезка
подъема графика водонасыщенности в области
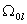 над графиком водонасыщенности
по МЛ модели на всей области
над графиком водонасыщенности
по МЛ модели на всей области 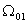 .
Уменьшение
.
Уменьшение 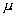 приводит также и к
возрастанию градиента водонасыщенности вблизи эксплутационной скважины после
прорыва воды по модели сопряжения. Из рис. 8, на котором изображены графики
приводит также и к
возрастанию градиента водонасыщенности вблизи эксплутационной скважины после
прорыва воды по модели сопряжения. Из рис. 8, на котором изображены графики
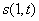 , соответствующие рис. 6,
видно, что график функции
, соответствующие рис. 6,
видно, что график функции 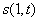 будет
иметь сложную структуру, зависящую от
будет
иметь сложную структуру, зависящую от 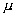 . Этот график состоит из трех основных участков. На первом участке
. Этот график состоит из трех основных участков. На первом участке
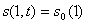 . Вследствии эффекта
недобегания этот участок в задаче сопряжения (4), (6), как правило, будет
больше соответствующего участка в МЛ модели на всей области
. Вследствии эффекта
недобегания этот участок в задаче сопряжения (4), (6), как правило, будет
больше соответствующего участка в МЛ модели на всей области
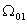 . На втором участке,
вследствии эффектов недобегания и выполаживания, прорыв воды в эксплутационную
скважину происходит по модели сопряжения с большим модулем градиента
водонасыщенности. При больших
. На втором участке,
вследствии эффектов недобегания и выполаживания, прорыв воды в эксплутационную
скважину происходит по модели сопряжения с большим модулем градиента
водонасыщенности. При больших 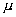 водонасыщенность на линии
водонасыщенность на линии 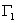 по модели сопряжения на втором участке будет больше соответствующего по МЛ
модели (при малых -
по модели сопряжения на втором участке будет больше соответствующего по МЛ
модели (при малых - 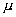 меньше).
На третьем - происходит сближение профилей
меньше).
На третьем - происходит сближение профилей 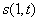 .
.
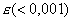 ,
,
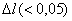 и больших
и больших
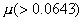 гораздо удобнее и экомичнее вместо модели сопряжения использовать МЛ модель.
В тоже время при больших
гораздо удобнее и экомичнее вместо модели сопряжения использовать МЛ модель.
В тоже время при больших 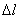 ,
,
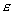 и малых
и малых
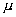 необходимо для получения более точных численных результатов применять модель
сопряжения (4), (6).
необходимо для получения более точных численных результатов применять модель
сопряжения (4), (6).