Всегда было принято считать, что знание логики обязательно для образованного человека. Сейчас, в условиях коренного изменения характера человеческого труда, ценность такого значения возрастает. Свидетельство тому - растущее значение компьютерной грамотности, одной из теоретических основ является логика.

Знание логики и умение применять ее к решению задач повышает культуру мышления, вырабатывает навык мыслить грамотно, развивает критическое отношение к своим и чужим мыслям.

Проблематика современной логики сложна и многообразна. Одна из главных проблем это то, что основное ее содержание формулируется на особом, созданном специально для своих целей искусственном языке.

Задачи, которые мы разобрали связаны с обычной деятельностью мышления. Эти задачи призваны не только оживить изложение, но и наглядно продемонстрировать, что логическое - это не только предмет специальных размышлений, но и то, с чем постоянно сталкивается каждый. Кроме того, примеры позволяют показать, что реальное мышление не сводится просто к логической последовательности. В процессе возникающих задач важным оказывается, как правило, все: и последовательность, и интуиция, и эмоции, и образное видение мира и многое другое.

Существуют разные способы формализации, как условий задачи, так и процесса её решения: алгебраический, табличный, графический и др. Каждый из этих способов обладает своими достоинствами.

Так, например, при применении алгебраического метода наиболее трудным является перевод текста задачи на язык формул. Далее, если вы знаете, логические законы и правила упрощения выражений, решение задачи сводится к формальным преобразованиям и приводит сразу к ответу, который остается лишь расшифровать, исходя из принятых вами обозначений.

Табличный метод очень нагляден, но не обладает универсальностью, т.е. предназначен для решения только одного типа задач. Кроме того, он требует анализа находящийся в таблице информации, умения сравнивать и сопоставлять.

Метод графов применяется тогда, когда между объектами, о которых идет речь в задаче, существует много связей. Граф позволяет наглядно представить эти связи и определить, какие из них не противоречат.

Метод диаграмм Эйлера-Венна позволяет графически решать математические задачи на основе применения теории множеств.

Как правило, задачу можно решить несколькими способами (методами). Чтобы выбрать наиболее простой и эффективный способ для каждой конкретной задачи, необходимо знать все эти способы.

Решение задач с помощью алгебры высказываний.

Для того, чтобы решать задачи этим методом надо знать не только основные логические законы, но и уметь их применять, а также правильно составлять тождественно истинные высказывания.

ЗадачаN1

В одной стране жили рыцари, которые всегда говорили правду, только правду и ничего кроме правды, и лжецы, которые всегда лгали. Однажды в страну проник шпион по имени Мердок, который, как и всякий шпион, иногда говорил правду, иногда лгал, в зависимости от того, что ему было выгодно. Шпион поселился с двумя жителями страны - рыцарем и лжецом. Всех троих арестовали в один день и привели на допрос. Никто не знал, кто из них кто. Они сделали следующие заявления:
А сказал: Я - Мердок.
В сказал: А говорит правду.
С сказал: Я не Мердок.

Кто же из них шпион - А, В или С ?

Решение:

Введем следующие переменные:
Пусть А_ш =А-шпион, тогда ¯A_ш =А - не шпион.
Пусть В_ш =В-шпион, тогда ¯B_ш = В- не шпион.
Пусть C_ш =С-шпион, тогда ¯C_ш = C- не шпион.

В наших обозначениях высказывания А, В, С записываются так:
А= А_ш ;В= А_ш ;С=¯C_ш .

По условиям задачи ясно, что из трёх высказываний истинным может быть либо одно (если шпион лжет), либо два ( если шпион говорит правду). Следовательно, возможны следующие варианты распределения истинных (И) и ложных (Л) высказываний:
ИИЛ V ИЛИ V ЛИИ V ЛЛИ V ЛИЛ V ИЛЛ=1.(*)

Посмотрим, что означает ИИЛ для введенных нами обозначений.

Высказывание пленника А истинно, следовательно, А_ш =1; высказывание пленника В истинно, следовательно, А_ш =1; высказывание пленника С ложно, следовательно, С_ш=1. То есть А_ш &А_ш &С_ш =1. Но А и С не могут одновременно быть шпионами, следовательно, это неверно и данная конъюнкция ложна.

Аналогично вариант ИЛИ "переводится" в наши обозначения так:
А_ш &¯А_ш &¯С_ш =1. Эта конъюнкция тоже ложна, поскольку А не может одновременно быть шпионом и не быть им.

Интерпретируем полностью формулу (*), опуская для кратности знак конъюнкции:
А_ш А_ш С_ш U А_ш ¯А_ш ¯C_ш U ¯А_ш А_ш ¯C_ш U ¯А_ш ¯А_ш ¯C_ш U ¯А_ш А_ш C_ш U А_ш ¯А_ш C_ш = 0 U 0 U 0 U ¯А_ш ¯C_ш U 0 U 0= ¯А_ш ¯C_ш =1.

То есть ни А ни С не шпионы, следовательно, шпион √ В. далее уже просто сделать вывод, что А - лжец, С - рыцарь.

2. Решение задач с помощью кругов Эйлера.

Задачи, которые можно решить с помощью кругов Эйлера нельзя решить иначе, по сравнению с табличным методом или при помощи графов. Этот способ решать задачи придумал в XVIII в. великий Леонард Эйлер. В этом разделе своей курсовой работы я рассмотрю несколько задач, которые можно решить этим методом. Этот метод прост, если в нем разобраться.

ЗадачаN2

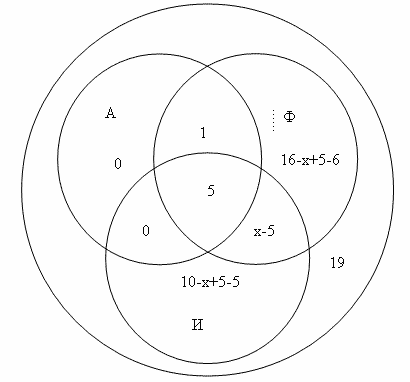
Из сотрудников фирмы 16 побывали во Франции,10-в Италии,6-в Англии; в Англии и Италии-5; в Англии и Франции -6; во всех трех странах - 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

Решение:

Нам известно, что во всех трех странах было 5 сотрудников. В Англии и Италии тоже 5, значит эти же сотрудники были и во Франции и поэтому в пересечении кругов А и И ставим 0. В Франции и Италии нам неизвестно поэтому пишем х-5 в пересечении кругов А и Ф. Т.к. в Англии было 6 человек, то 6-5-1=0 пишем 0,во Франции 16-х+5-6 и Италии 10-х+5-5 и всего в фирме 19 сотрудников, то остается составить и решить уравнение:
1+16-х+5-6+5+х-5+10-х+5-5=19, отсюда х=7, значит в Италии и Франции побывало 7-5=2 сотрудника фирмы.

4. Решение задач с помощью графов.

Граф - один из видов моделей, отражающих взаимодействие объектов или систем.

Графом называют схему, в которой обозначаются только наличие объектов (элементов системы) и наличие и вид связи между объектами.

Объекты представляются в графе вершинами (на схеме они обозначаются кружочками, прямоугольниками и т.п.). Связи между объектами представляются, если связь однонаправленная (обозначается на схеме линиями со стрелками) или ребрами, если связь между объектами двусторонняя ( обозначается на схеме линиями без стрелок).

Например, если нужно представить в графе, что из состояния А в состояние В возможен переход под воздействием V, то это можно изобразить так:

Если нужно представить, что к-тый участник соревнования занял n-е место ( или, что то же самое, n-е место занял к-тым участником), это можно изобразить так:

Задача N11.
Марина, Лариса, Жанна и Катя умеют играть на разных инструментах( пианино, виолончели, гитаре, скрипке), но каждая только на одном. Они же знают иностранные языки (английский, французский, немецкий и испанский), но каждая только один. Известно:
1. Девушка, которая играет на гитаре говорит по √ испански.
2. Лариса не играет ни на скрипке ни на виолончели и не знает английского языка.
3. Марина не играет ни на скрипке, ни на виолончели и не знает ни немецкого, ни английского.
4. Девушка, которая говорит по - немецки, не играет на виолончели.
5. Жанна знает французский язык, но не играет на скрипке.
Кто на каком инструменте играет и какой иностранный язык знает?

Решение:

Из пятого условия, что Жанна знает французский язык, рисуем стрелку. Из третьего условия, что Марина не знает ни немецкого, ни английского, а французский знает Жанна, то Марина знает испанский и рассматривая первое условие она играет на гитаре. Из условия N2 видим, что Лариса играет на пианино, т.к. Марина играет на гитаре, а на других инструментах она играть не умеет, и значит, она говорит по-немецки.

Т.к. Жанна не играет на скрипке, то остается один инструмент, на котором она может играть это виолончель. Тогда Катя играет на скрипке, и знает английский язык.

Мною были рассмотрены различные методы решения содержательных логических задач, это такие методы как, метод решения задач при помощи таблицы, при помощи кругов Эйлера, при помощи алгебры высказываний и при помощи графов. Из этого можно сделать вывод, что, решая, какую-либо задачу не надо останавливаться на каком-то одном приеме, ведь вероятнее всего эту же задачу можно решить и другим методом, который будет и легче и проще для данной задачи. Задачи, которые я разобрала в своей курсовой работе, можно предлагать и школьникам и студентам высших заведений. Я считаю, что для школы, тема моей курсовой работы актуальна на дополнительных занятиях по математике, а также для школ с углубленным изучением математики.

Литература
1. Занимательная математика. 5 - 11 классы. (Как сделать уроки математики не скучными)/ Авт.-сост. Т. Д. Гаврилова. - Волгоград: Учитель, 2005. -96 с.
2. Лихтарников Л. М., Сукачева Т.Г. Математическая логика /Курс лекций / Оформление обложки А. Олексенко, С. Шапиро. - СПб.: Издательство "Лань",1998. - 288с.
3. Лыскова В.Ю., Ракитина Е.А. Логика в информатике. - М.: Лаборатория базовых знаний, 2001. - 160 с.: ил. Серия "Информатика".