Теория чисел является одним из древнейших разделов математики. Она возникла как наука, изучающая свойства натуральных чисел. Понятие натурального числа и арифметических действий нал числами является одним из первых математических абстракций, имеющим важнейшее значение для математики, других наук и всей практической деятельности человечества.

Некоторые результаты о простых числах были получены ещё в Древней Греции. В книге Евклида "Начала" содержится доказательство бесконечности множества простых чисел. Древнегреческий учёный Эратосфен нашел способ составления таблиц простых чисел, названный позднее " решетом Эратосфена".

Проблемы, связанные с распределением простых чисел в натуральном ряде обычно являются очень трудными. Многие великие математики проявляли к ним большой интерес. Существенный прогресс в исследовании этих проблем был достигнут в середине XIX века русским ученым П. Л. Чебышевым.

Функция П(X). Неравенство Чебышева.

Рассмотрим множество натуральных чисел N.



Определение: Каждое натуральное число n, n>1,принадлежащее множеству N называется простым, если оно не имеет других натуральных делителей, кроме 1 и n.

Число простых чисел, меньших или равных X, мы будем обозначать через П(X), так что П(X)= 1.Для каждого данного X можно выписать все простые числа p≤X и определить их число, т.е. вычислить П(X). Однако мы не получим при этом представления о том, как меняется функция П(X) с увеличением X, т.е. представления о том, как быстро увеличивается число простых чисел, если брать всё большие отрезки натурального ряда.

В 1848 и 1850 годах появились две замечательные работы П. Л. Чебышева, в которых исследовался вопрос о порядке роста функции П(X).

Теорема Чебышева: Существуют две постоянные a и b, такие, что 01 и для всех x𕟴 выполняются неравенства: a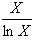<П(X) < b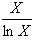

П. Л. Чебышев показал, что в качестве a и b можно взять значения a=0,921, b=1,106 сравнительно близкие к 1.

Из теоремы Чебышева следует, что при увеличении X отношение

Работы П. Л. Чебышева поставили перед математиками задачу найти постоянные a и b более близкие к 1, т.е. получить асимптотическую формулу П(X)∼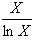, выражающую, что lim=1.

Равенство данного предела единице была доказана Чебышевым, но существование его он показать не смог. Это сделали в 1896 году независимо друг от друга Ж.Адамар и Ш.Ж. де ла Вале-Пуссен.

Формула Мейсселя.

Остановимся на некоторых точных формулах для П(X), позволяющих вычислять значения этой функции, не составляя предварительно таблицы самих простых чисел.

Обозначим через Ф(X,Y) число простых чисел, меньших или равных X, не делящихся на простые числа, меньшие или равные Y.

Теорема Мейсселя: П(X)= Ф(X,X^1/3 )-+ 1/2(П(X^1/2)+П(X^1/3)-2)(П(X^1/2)-П(X^1/3)+1).

Эта формула была получена Мейсселем в 1870 году и является очень удобной для вычисления значений П(X).

Вычисление значений функции П(X) обычно осуществляется с помощью данной формулы или аналогичных формул такого рода. Известны формулы выражающие П(X) через Ф(X, X^1/n ) при n>3 и значения П(Y) при сравнительно небольших значениях Y, однако эти формулы очень громоздки.

Пример: Найти число простых чисел в пределах от 1 до 1250.

Ф(1250,)=287.Между =10,7... и =35,3 лежат простые числа 11,13,17,19,23 и 31. П (10,7)=4, П(35,3)=11. Находим при X=1250.

=П(1250/11)+П(1250/13)+П(1250/17)+П(1250/19)+П(1250/23)+П(1250/29)+П(1250/31)=35

П(1250)=287-135+1/2(11+4-2)(11-4+1)=204.

Простые числа в арифметических прогрессиях.

Определение: Арифметической называется такая последовательность, в которой каждый последующий член отличается от предыдущего на одно и тоже число.

Арифметические прогрессии являются наиболее простым примером подпоследовательности последовательности натурального ряда.

Возьмём ,например, арифметическую прогрессию с разностью 10.

7,17,27,37,47,57,67,77,87,97,...

Видно, что в начале среди её членов встречается сравнительно много простых чисел(подчёркнутые члены). Будут ли простые числа, содержащиеся в этой прогрессии, образовывать бесконечное множество или начиная с некоторого места простые числа больше уже встречаться не будут?

Ответ на этот вопрос дал в 1837 году Дирихле. Оказывается, что не только в данной прогрессии, но и в любой другой прогрессии, у которой начальный член взаимно прост с разностью содержится бесконечное число простых чисел.

Теорема Дирихле: Если (k,l)=1, то прогрессия l,l+k,l+2k,l+3k,... содержит бесконечное число простых чисел.

В 1949 году Сельбергом было опубликовано элементарное доказательство этой теоремы. Для отдельных частных случаев теорема Дирихле может быть получена совершенно элементарно, например, на основании двух вспомогательных теорем:

Теорема: Множество простых чисел вида 4t+3 бесконечное множество.

Теорема: Множество простых чисел вида 4t+1 бесконечное множество.

Однако, ничего это не говорит о том, как далеко от начала прогрессии начнут встречаться простые числа. В этом отношении интересный результат был получен в 1944 году Ю. В. Линником. Теорема Линника устанавливает границу для наименьшего простого числа любой заданной прогрессии.

Теорема Линника: Существует постоянное число с, такое, что при любых взаимно простых k и l (1≤ l ≤ k ) наименьшее простое число, принадлежащее прогрессии l,l+k,l+2k,l+3k... не превосходят k^c .

Арифметические прогрессии представляют собой значения линейной функции f(t)=kt+l при t=1,2,3... Если вместо линейной функции взять другую функцию f(t), то можно так же составить задачу: содержит ли последовательность f(1), f(2), f(3),... бесконечное множество простых чисел?

Современная теория чисел пока не сумела решить этот вопрос. Трудность этой проблемы не связана с особенностью функции f(t), проблема будет, если перейти и к другому неприводимому над полем рациональных чисел многочлену второй степени at² +bt+c, где(a,b,c)=1. Ещё труднее становится проблема, если перейти к многочленам более высокой степени. До сих пор ни для одного многочлена с целыми коэффициентами f(t)=a₀ tⁿ +a₁ t^n-1 +...+a_n степени n>1 не удалось установить существование бесконечного числа простых чисел.

Итак, современной теории чисел удаётся исследовать распределение простых чисел только в арифметических прогрессиях, да и то далеко не полностью.

В теории чисел широко используются методы теории функций, алгебры, геометрии, теории вероятностей. Особенно большое значение имеют аналитические методы, основанные на применении к задачам теории чисел теории функции комплексного переменного.

Решение теоретико-числовых задач стимулировало развитие других разделов математики. Например, развитие методов, связанных с изучением распределения простых чисел, в значительной мере способствовало развитию теории целых и мероморфных функций.

Теория чисел в основном является наукой теоретической. Однако её результаты и методы успешно применяются в других разделах математики, многих других науках, а также при решении ряда практических задач.

Литература

1. А. А. Бухштаб "Теория чисел" издательство "Просвещение" 1966г.
2. А. Я. Куликов "Алгебра и теория чисел " Учебное пособие для педагогических институтов- М.:Высшая школа 1979г.
3. А. А. Карацуба "Основы аналитической теории чисел" второе издание-М.:Наука. Главная редакция физико-математической литературы 1983г.
4. А. Б. Шидловский "Введение в теорию чисел" М.:Издательство Московского института 1984г.
5. К. Чандрасекхаран "Введение в аналитическую теорию чисел "Издательство "Мир" 1974г.