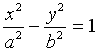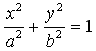Приложение 8
КОНСПЕКТ ОТКРЫТОГО УРОКА
Обобщающий урок
по темам «Многогранники», «Тела вращения»
Цели:
- Приведение в систему знаний учащихся по темам «Многогранники», «Тела вращения", систематизация учебного материала по разделам.
- Отработка понятийного аппарата, определений, символики, формул.
- Развитие пространственного воображения и пространственного представления учащихся.
№ п/п
Этап и содержание урока
Методические замечания
1.
Организационный момент.
Целевая установка урока
2.
Популяризация урока: сообщение темы, целей, задач учебного занятия.
Название темы на доске
3.
Актуализация знаний.
Вспомним основные пространственные фигуры, опишем их основные характеристики по схеме:
а) определение
б) основные компоненты и их характеристики
в) основные формулы
г) практическая направленность объекта и его применение.I. Многогранники:
- пирамида (доклад)
- призма (доклад)
- параллелепипед (доклад)
II. Тела вращения:
- цилиндр (доклад)
- конус (доклад)
- шар (доклад)
( В процессе слушания докладов учащиеся свободно помогают друг другу и приводят примеры моделей аналогичных многогранников и тел вращения, встречающихся в реальной жизни).
Прослушивание мини-докладов учащихсяДемонстрация моделей, схем, чертежей, рисунков
Развитие устной речи учащихся по отработке понятийного аппарата темы4.
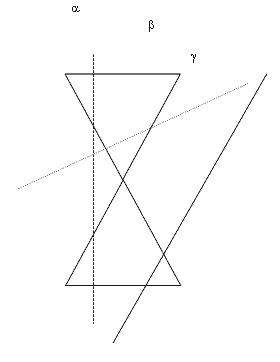
Систематизация учебного материала. Конические сечения. Рассмотрим одну из поверхностей вращения - коническую поверхность (К). Исследуем К на сечения и вместе попытаемся определить происхождение кривых второго порядка:
Рассмотрим проекционный чертеж. По этому чертежу построим стереометрическое изображение полученных сечений. Плоскости a , b , g пересекают коническую поверхность, в результате образуются кривые линии:
- К
a = G (гипербола) :
- К
b = E ( эллипс):
- К
g = Р (парабола):
Частным случаем эллипса является окружность.
Вывод: в се планиметрические фигуры есть результат сечения стереометрических фигур в пространстве различными плоскостями сечения.
Математики имеют обыкновение изучать вещи, кажущиеся совершенно бессмысленными. Но проходят века, и исследования приобретают огромную научную ценность. К примеру, исследования, проводимые древними греками, кривых второго порядка, отличных от окружности, не имели до XVII в. практического приложения.
Астроном Иоган Кеплер , последователь Коперника, утверждал, что не Солнце движется вокруг Земли, а Земля движется вокруг Солнца, причем он доказал, что планеты движутся по эллипсам, а Солнце находится в фокусе этих эллипсов.
Основателем современного учения о кривых второго порядка по праву считают великого немецкого художника и ученого - Альбрехта Дюрера (1471-1528) - одного из титанов эпохи Возрождения. Эта эпоха дала много замечательных людей с разносторонними интересами. В их числе А. Дюрер (Германия), Л. Винчи (Италия). Дюрер занимался архитектурой, градостроительством, гуманитарными науками. Его вклад в историю точных наук неоценим. Он является основателем учения о правильных многогранниках, теории кривых второго порядка. Его отличали оригинальность, глубина мышления, логика и доказательность утверждений.
Дюреру А. принадлежат великие слова:
«Никакое человеческое исследование не может считаться истинной наукой, пока оно не прошло через математическое доказательство».
Как художник, Дюрер создал бессмертные образцы портретной живописи, графики, гравюрного искусства. Он отличался необыкновенной широтой интересов, разносторонностью знаний, первым в Германии он обратился к разработке основ искусства - теории перспективы и учению о пропорциях человеческого тела.
Ученые древности внесли большой вклад в развитие теории многогранников. Они утверждали, что в основе мироздания лежат многогранники. Древнегреческий ученый Платон считал, что атомы 4 элементов, из которых построен мир, имеют форму правильных выпуклых многогранников:
Огонь - тетраэдр : грани - правильные треугольники, в каждой вершине по три ребра
Земля - куб : грани - квадраты, в каждой вершине по три ребра.
Воздух - октаэдр : грани - правильные треугольники, в каждой вершине по 4 ребра.
Вода - икосаэдр : грани - правильные треугольники, в каждой вершине по 5 ребер.
Платон в те далекие времена на чисто интуитивном уровне утверждал, что весь мир в целом построен в форме додекаэдра: «Земля, если взглянуть на нее сверху, похожа на мяч, сшитый из 12 кусков кожи».
Рассмотрим цилиндрическую поверхность. Произведем вырезку этой поверхности двумя параллельными плоскостями. Выполним модернизацию: разрежем поверхность поперек, перевернем один край и снова склеим. Мы получили лист Мёбиуса. Это замечательная фигура является примером односторонней поверхности. Она имеет всего один край, а если попытаться закрасить ее с одной стороны, то ничего из этого не выйдет. Лучше сразу все опустить в ведро с краской. Вопрос: что произойдет с листом Мёбиуса, если разрезать его посередине ?
В математике есть специальный раздел, изучающий такие поверхности. Топология - раздел математики, изучающий те свойства фигур, что не меняются при непрерывных деформациях.
Эти свойства листа Мёбиуса не мог не заметить знаменитый художник Эшер, который посвятил этому серию своих картин, где пространство и время находятся в определенной противоречивой взаимосвязи. Демонстрируются произведения Эшера «Водопад», «Бельведер», «Ящерицы», «Поднимаясь и опускаясь», «Вверху и внизу» и др.
Формирование пространств. представлений
Работа с чертежными инструментами по отработке графической культуры
Отработка точности и аккуратности построений
Вывод делают учащиеся
Демонстрации портретов ученых И.Кеплера, А. Дюрера, Л.Винчи
Демонстрация репродукций и произведений искусства художников
На доске вместе с учащимися создаётся схема взаимосвязей элементов мироздания и многогранников
Работа с дидактическими таблицами и учебником
Демонстрация превращения куска цилиндрической поверхности в лист Мёбиуса
Домашнее задание № 1
Демонстрации картин, литографий, орнаментов, гравюр Эшера
5.
Практическая работа.
Пространство и плоскость. Как изобразить на плоскости пространственные фигуры ? Для этого очень часто используют шаблоны-трафареты: цилиндры и конусы, параллелепипеды и 4-угольные пирамиды, призмы и пирамиды.
Практическая работа
Домашнее задание № 2
6.
Образование тел вращения.
Мини-доклад (Давыдова М.): образование тел вращения вокруг оси, нахождение объемов тел вращения по схеме, знакомство с новыми пространственными фигурами.
Тор: V = 2 Π2 r2 R , S = 4 Π r R
Задача 1 . Как найти объем фигуры, образованной вращением планиметрической фигуры вокруг оси MN ?
Выступает ученик с индивидуальным заданием
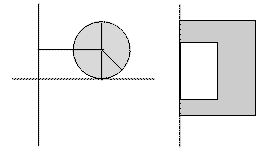
Тор
(демонстрация наглядности)Формирование пространств. воображения
7.
Задача 2. (Исследовательская задача). Составьте схему перехода от понятия «многогранник» к понятию «куб», осуществляя каждый переход через условие, характерное свойство:
Многогранник -> призма -> прямая призма -> правильная призма -> параллелепипед -> куб.
Формирование алгоритмической культуры
Учащиеся выявляют свойства, характерные для данного понятия
8.
Задача 3. Исследование изменения объемов многогранников при изменении их линейных размеров. Выберите определенных размеров куб, параллелепипед, пирамиду с квадратом в основании и шар. Вычислите их объем. Если увеличить линейные размеры этих тел в 2 раза, то чему станут равны их объемы? Заполните таблицу, сделайте соответствующие выводы.
Найдите отношения:
Vi / V ' i = ... , где i =1,4
Вывод: Если увеличить линейные размеры многогранника в k раз, то его объём увеличится в k 3 раза.
Заполнение таблицы, самостоятельное формулирование выводов
9.
Занимательная часть.
Отгадайте кроссворды по темам «Многогранники. Пирамида»
Раздаточный материал.
Домашнее задание № 3
10.
Домашнее задание.
Прокомментировать № 1,2,3
11.
Оценивание учащихся.
12.
Подведение итогов.
Выводы.
Краткое обобщение урока с позиции достижения его цели.
Дидактический материал к уроку
Исследовательская задача
№
название
многогранника
старые
данные
старый
объем
новые
данные
новый
объем
1
куб
a = 2
V1 =
a' =
V'1 =
2
параллелепипед
a = 2
b = 1
c = 3
V2 =a' =
b' =
c' =
V'2 =3
пирамида
с квадратом
в основанииh = 3
a = 2V 3=
h' =
a' =V'3 =
4
шар
r =
V4 =
r' =
V'4 =
Кроссворд по теме «Многогранники. Пирамида »
По горизонтали : 1. Количество сходящихся ребер у октаэдра. 2. Грань додекаэдра. 3. Боковая грань усеченной пирамиды. 4. Правильный многогранник. 5. Сечение, проходящее через вершину пирамиды и диагональ основания.
По вертикали: 2. Граница многогранника. 6. Правильная треугольная пирамида. 7. Перпендикуляр, опущенный из вершины пирамиды на плоскость основания. 8. Элемент пирамиды. 9. Пирамида, у которой основание правильный многоугольник, а вершина проецируется в его центр.
Литература: Белл Э.Т. Творцы математики. - М.: Просвещение, 1991; Болгарский Б.В. Очерки по истории математики. - Минск: Высшая школа, 1974; Глейзер Г. История математики в школе, IX - X кл. - М.: Просвещение, 1983; Гусев В. А. и др. Внеклассная работа по математике в 6-8 кл. - М.: Просвещение, 1977; Курант Р., Роббинс Г. Что такое математика? - М.: Просвещение, 1967; Левитин К. Геометрическая рапсодия. - М.: Знание, 1976; Матвиевская Г. П. Альбрехт Дюрер - ученый. - М.: Наука, 1987; Таллер А. Сюрпризы листа Мёбиуса // Квант, 1978. - № 6; Штейнгауз Г. Математический калейдоскоп. - М.: Наука, 1981; Энциклопедический словарь юного математика. - М.: Педагогика, 1989.