Практическое занятие 5

МАТЕМАТИЧЕСКИЕ СУЖДЕНИЯ, УМОЗАКЛЮЧЕНИЯ. МЕТОДИКА РАБОТЫ С ТЕОРЕМОЙ. МАТЕМАТИЧЕСКИЕ ДОКАЗАТЕЛЬСТВА

1. Аксиомы. Постулаты. Математические предложения. Утверждения. Примеры аксиом, математических предложений, математических утверждений.
2. Назовите структурные элементы теоремы. Формы теорем (категоричная и условная). Приведите примеры.
3. Какова взаимосвязь между прямой, обратной, противоположной, обратной противоположной теоремами. Необходимость и достаточность.
4. Математические доказательства: содержательные (неформальные) и формальные доказательства. Оформление доказательств теорем.
5. Метод доказательства от противного и его сущность.
6. Основные этапы работы над теоремой.
7. Логико-математический анализ теоремы.

Практические задания

1. Выполните логико-математический анализ утверждения: “Вертикальные углы равны”. В какой форме сформулировано утверждение? Сформулируйте утверждение в импликативной форме. Выделите разъяснительную часть. Выделите условие и заключение утверждения. Установите в зависимости от числа условий и заключений, является ли данное утверждение простым или сложным.Результаты анализа оформите в виде таблицы.

Таблица 1

Импликативная форма теоремы Если ..............................................., то .........................…………...........
Структура теоремы	Разъяснительная часть: ………............................ Условие: .................................………………............... Заключение: ..............................………………............
Характеристика теоремы: Теорема ............ , так как ..........................................................

 2. Разработайте карточки таблицы (с пропусками) для доказательства любой из теорем школьного курса геометрии (по усмотрению преподавателя).
3. Составьте план работы над теоремой: “Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180 0 , то прямые параллельны”. Разработайте методику ее доказательства и оформите доказательство в тетради.
4. Рассмотрите вопрос о способах доказательств геометрических теорем. Проиллюстрируйте примерами наиболее рациональные из них.
Замечание . Одним из таких способов является запись доказательства с помощью таблицы, в которой отражаются этапы доказательства. Замена текста многоточиями позволяет получить карточку, которая может быть использована при проведении самостоятельной работы. В этом случае, заполнив пропуски, количество которых дает возможность варьировать степень сложности, учащиеся должны восстановить “цепочку“ доказательства.
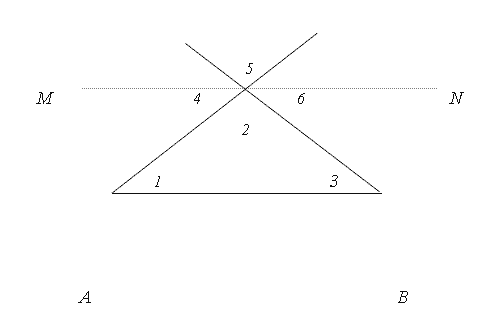
5. Докажите, что сумма углов треугольника равна 180 0 . Последовательность шагов доказательства оформите в таблицу 2.

Таблица 2

№ п/п	Утверждения	Обоснования
1	MN // AB	По построению
2	< 1 = < 6; < 3 = < 4	Углы с сонаправленными сторонами
3	< 5 = < 2	Вертикальные углы
4	< 4 + < 5 + < 6 = 180 0	< MCN - развернутый
5	< 1 + < 2 + < 3 = 180 0	Утверждения 2,3,4.

 

Таблица 3

№ п/п	Утверждения	Обоснования
1	MN // AB	..................................................................
2	.....................................	Углы с сонаправленными сторонами
3	< 5 = < 2	..................................................................
4	.....................................	< MCN - развернутый
5	.....................................	Утверждения 2,3,4.

 

6. Составьте дидактический материал по закреплению теорем и раскройте методику работы с разрезными теоремами (на примере любой теоремы школьного курса математики.).

  Таблица 4

Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Условие	Чертеж
Доказательство: ……………………………. . . . . . . . . . . . . . . . .

7. Установите взаимосвязь ложности и истинности разных видов теорем (на примере одной из теорем школьного курса математики) путем заполнения таблицы 5:

Таблица 5

№ п/п	Вид	Формулировка		Контрпример		1 или 0
Теорема (импликативная форма): . . . . . . . . . . . . . . . . . . . . . . . . . .
1	P = G		. . . . . . . . .	. . . . . . . . .	. . . . . . . . .
2	G = P		. . . . . . . . .	. . . . . . . . .	. . . . . . . . .
3	_     _ P = G		. . . . . . . . .	. . . . . . . . .	. . . . . . . . .
4	_     _ G = P		. . . . . . . . .	. . . . . . . . .	. . . . . . . . .