МЕТОДИКА ПРЕПОДАВАНИЯ МАТЕМАТИКИ

Одной из основных задач современного школьного обучения является развитие мышления учащихся. В отличии от традиционного мышления, современное обучение характеризуется стремлением сделать развитие мышления школьников управляемым процессом, а основные приемы мышления - специальным предметом усвоения.

Мышление характеризуют качества научного мышления:

- гибкость - умение целесообразно варьировать способы решения познавательной проблемы, легкость перехода от одного пути решения проблемы к другому; умение выходить за границы привычного способа действия, находить новые способы решения проблемы при изменении задаваемых условий; умение перестраивать систему усвоенных знаний по мере овладения новыми знаниями и накопления опыта;
- оригинальность - высший уровень развития нешаблонного мышления, необычность способов решения учащимися известных задач. Оригинальность мышления - следствие глубины мышления;
- целесообразность - стремление осуществлять разумный выбор действий при решении какой-либо проблемы, постоянно ориентируясь на поставленную этой проблемой цель, а также в стремлении отыскать наиболее кратчайшие пути ее достижения;
- рациональность - склонность к экономии времени и средств для решения поставленной проблемы, стремление отыскать оптимально простое в данных условиях решение задачи, использовать в ходе решения схемы, символику и условные обозначения;
- широта - способность к формированию обобщенных способов действий, имеющих широкий диапазон переноса и применения к частным, нетипичным случаям; умение охватить проблему в целом; обобщить проблему, расширить область приложения результатов, полученных в процессе ее разрешения; умение классифицировать и систематизировать изучаемые математические факты и использовать аналогию и обобщение как методы решения задач;
- активность - постоянство усилий, направленных на решение некоторой проблемы, желание обязательно решить данную проблему, изучить различные подходы к ее решению и др.;
- критичность - умение оценить правильность выбранных путей решения поставленной проблемы, получаемые при этом результаты с точки зрения их достоверности и значимости; умение найти и исправить собственную ошибку, проследить заново все выкладки или ход рассуждения, чтобы натолкнуться на противоречие, помогающее осознать причину ошибки;
- доказательность - умение терпеливо относиться к собиранию фактов, достаточных для вынесения какого-либо суждения; стремление к обоснованию каждого шага решения задачи; умение отличать достоверные результаты от правдоподобных;
- организованность памяти - способность к запоминанию, долговременному сохранению, быстрому и правильному воспроизведению основной учебной. При обучению учащихся математике следует развивать как оперативную, так и долговременную память, обучать учащихся запоминанию наиболее существенного, общих методов и приемов решения задач, доказательству теорем; формировать умения систематизировать свои знания и опыт. Организованность памяти формируется у школьников особенно эффективно, если запоминание каких-либо фактов основано на их понимании.

Не нуждаются в особых комментариях качества научного мышления: ясность, точность, лаконичность устной и письменной речи. Совокупность всех указанных качеств мышления называют научным стилем мышления.

4. 2. РОЛЬ МЫШЛЕНИЯ В ОБУЧЕНИИ МАТЕМАТИКЕ. МАТЕМАТИЧЕСКОЕ МЫШЛЕНИЕ

Специфика предмета математики такова, что ее изучение существенно влияет на развитие мышления школьников. Развитие мышления школьников тесно связано с формированием приемов мышления в процессе их учебной деятельности. Эти приемы мышления (анализ, синтез, обобщение и др.) выступают также как специфические методы научного исследования, особенно ярко проявляющиеся при обучении математике, как одного из базовых школьных предметов.

Особенности математики наиболее полно раскрываются в единстве двух ее сторон: математика как определенная научная деятельность и математика как теория, являющаяся результатом этой деятельности.

Выделяются следующие составные части учебной математической деятельности: математизация эмпирического материала; логическая организация математического материала; применение теории. В более детальной расшифровке элементы математической деятельности можно представить таким образом:
1)целенаправленное накопление эмпирического материала;
2)выбор математического языка, описание эмпирического материала на языке математики;
3)первичная систематизация математического материала, группировка его по тем или иным общелогическим признакам (сходству, степени общности и т. д.);
4)частичная аксиоматизация математического материала, построение фрагмента математической теории;
5)применение математического материала;
6)применение частично аксиоматизированного математического материала (фрагмента теории);
7)применение теоретического материала нескольких математических разделов.

Под эмпирическим материалом подразумеваются окружающие нас реальные объекты, к изучению которых стремятся применить методы математики, или объекты другой научной области (физики, химии, астрономии, биологии и т. д.), или специально приготовленный для целей обучения дидактический материал, или математический материал в случае, когда он подвергается изучению с помощью других математических средств.

Математическое образование представляет собой сложный процесс, который формируется в деятельности школьников. Основными целевыми компонентами математического образования в школе являются:
а) усвоение школьниками системы математических знаний;
б) овладение школьниками определенными математическими умениями и навыками;
в) развитие мышления учащихся.

Мыслительная деятельность школьников выполняется с помощью мыслительных операций: сравнения, анализа и синтеза, абстракции, обобщения и конкретизации.

Сравнение - это сопоставление объектов познания с целью нахождения сходства (выделения общих свойств) и различия (выделения особенных свойств) между ними. Эта операция лежит в основе всех других мыслительных операций.

Анализ - это мысленное расчленение предмета познаний на части.

Синтез - мысленное соединение отдельных элементов или частей в единое целое. В реальном мыслительном процессе анализ и синтез всегда выполняются совместно.

Абстракция - это мысленное выделение каких-либо существенных свойств и признаков объектов при одновременном отвлечении от всех других их свойств и признаков. В результате абстракции выделенное свойство или признак сам становится предметом мышления.

Обобщение можно рассматривать:
1) как мысленное выделение общих свойств (инвариантов) в двух или нескольких объектах и объединение этих объектов на основе выделенной общности;
2) как мысленное выделение существенных свойств объекта в результате анализа их в виде общего понятия для целого класса объектов (научно-теоретическое общение).

Конкретизация также может выступать в двух формах:
1) как мысленный переход от общего к единичному, частному;
2) как восхождение от абстрактно-общего к частному путем выявления различных свойств и признаков объекта.

Различают три вида мышления:
1. Наглядно-действенное (познание объектов совершается в процессе практических действий с этими объектами, характерно для детей младенческого возраста).
2. Наглядно-образное (мышление с помощью наглядных образов, свойственно детям дошкольного возраста).
3.Теоретическое мышление (в форме абстрактных понятий и суждений, характерно для детей школьного возраста).

С развитием математики как науки и методики преподавания математики изменилось содержание, которое вкладывалось в понятие “математическое мышление”, существенно возросла роль проблемы развития мышления в процессе обучения математике.

Математическое мышление является не только одним из важнейших компонентов процесса познавательной деятельности учащихся, но и таким компонентом, без целенаправленного развития которого невозможно достичь высоких результатов в овладении школьниками системой математических знаний, умений и навыков. К сожалению, в настоящее время не выявилось единого подхода к трактовке понятия мышления, к объяснению тех механизмов, которые им управляют.

Формирование математического мышления школьников предполагает целенаправленное развитие всех качеств, присущих естественнонаучному мышлению, комплекса мыслительных умений, лежащих в основе методов научного познания, в органическом единстве с формами проявления мышления, характеризующихся спецификой предмета математики.

Известный математик и педагог А. Я. Хинчин выделяет следующие признаки математического мышления:
1)доминирование логической схемы рассуждения;
2)лаконизм мышления: предельная скупость, суровая строгость мысли и ее изложения;
3)четкая расчлененность хода рассуждения;
4)точность символики.

Основным определяющим признаком культуры математического мышления он считал полноценность аргументации, которя предполагает:
1)освоение учеником идеи доказательства;
2)умение пользоваться определениями понятий (осознавать их логическую структуру, уметь выполнять действия подведения под понятие и выведение следствий);
3)умение работать с теоремами (понимать логическое строение теоремы, сущность прямой и обратной теоремы и т. д.);
4)владение общими логическими методами доказательства: аналитическим, синтетическим, методом от противного, полной индукцией, математической индукцией;
5)владение частными методами и приемами, характерными для той или иной темы.

Органическое сочетание и повышенная активность различных компонентов мышления проявляются в особых способностях человека (математических, организаторских, педагогических и т.д.), что дает ему возможность успешно осуществлять творческую деятельность в самых разнообразных областях.

При обучении математике активно формируются такие качества мышления, как гибкость, оригинальность, глубина, широта, активность, критичность, доказательность, самостоятельность. Творческий уровень изучения математики формирует математические способности.

Математические способности - это определенная совокупность некоторых качеств творческой личности, сформированных в процессе математической деятельности.“

Синдром математической одаренности” школьников (по Крутецкому) характеризуется: быстрым схватыванием математического материала, тенденцией мыслить сокращенно, свернутыми структурами, стремлением к своеобразной экономии умственных усилий, наличием ярких пространственных представлений.

к плану

4.3. МАТЕМАТИЧЕСКОЕ ПОНЯТИЕ И ЕГО ХАРАКТЕРИСТИКИ

Мышление есть активный процесс отражения объективного мира в сознании человека. Всякое явление, любой процесс представляет собой единство содержания и формы. Структуру отдельных мыслей и их особых сочетаний называют формами мышления. Основными формами мышления являются понятия, суждения, умозаключения. Понятия являются одной из главных составляющих содержания любого предмета, в том числе и предметов математического цикла. Полноценное изучение математических понятий систематизирует знания учащихся, способствует более глубокому освоению предмета. Первостепенная задача учителя математики пи изучении любой темы – формирование понятийного аппарата темы.

Понятие - форма мышления, в которой отражены существенные (отличительные) свойства объектов изучения. Понятие считается правильным, если оно верно отражает реально существующие объекты.

Каждое понятие может быть рассмотрено по содержанию и объему. Содержание понятия раскрывается с помощью определения, объем - с помощью классификации. Посредством определения и классификации отдельные понятия организуются в систему взаимосвязанных понятий.

Содержание понятия - это множество всех существенных признаков данного понятия.

Объем понятия - множество объектов, к которым применимо данное понятие.

Например, понятие «треугольник» соединяет в себе класс всевозможных треугольников (объем этого понятия) и характеристическое свойство - наличие трех сторон, трех вершин, трех углов (содержание понятия); понятие «уравнение» соединяет в себе класс всевозможных уравнений (объем понятия) и характеристическое свойство - равенство, содержащее одну или несколько переменных (содержание понятия).

Существенные свойства (характеристические) - это такие свойства, каждое из которых необходимо, а все вместе достаточны для характеристики объектов, принадлежащих понятию. Мы имеем понятие о некоторой вещи, если знаем и можем словесно выразить, какие условия необходимы и вместе с тем достаточны для ее однозначного определения. Однако, не каждое необходимое условие является достаточным и не каждое достаточное условие является необходимым. Например, равенство двух углов является необходимым условием для того, чтобы эти углы были вертикальные, но не является достаточным. Процесс конструирования понятий заключается в поиске такого числа необходимых условий, которое было бы достаточно для однозначного определения требуемого класса вещей. Совокупность этих условий и принимают за содержание понятия.

Содержание понятия раскрывается с помощью определения, объем - с помощью классификации. Так, содержанием понятия квадрата является совокупность условий «быть четырехугольником», «иметь равные стороны», «иметь равные углы». Квадрат можно определить как четырехугольник с равными сторонами и равными углами.

Например, для понятия “параллелограмм” содержание будет представлено следующими свойствами:
а) противоположные стороны равны и параллельны;
б) противоположные углы равны;
в) диагонали в точке пересечения делятся пополам и др.

Объем понятия “параллелограмм” представлен множествами следующих четырехугольников:
1) собственно параллелограммы;
2) ромбы;
3) прямоугольники;
4) квадраты (рис. 5).

Рис. 5. Объем понятия “параллелограмм”

Содержание понятия четко определяет его объем, и наоборот, объем понятия вполне определяет его содержание. Таким образом, изменение в содержании понятия влечет за собой изменение в его объеме, и наоборот. Между содержанием и объемом понятия существует в некотором смысле обратная связь: с увеличением содержания понятия “параллелограмм” (диагонали взаимно перпендикулярны) сразу уменьшается его объем (остаются лишь ромб и квадрат); если уменьшить содержание этого понятия (потребовать параллельности только двух противоположных сторон), увеличится его объем (к названным четырехугольникам добавится трапеция).

сли объем одного понятия содержится в объеме другого понятия, то второе понятие называется родовым по отношению к первому понятию, а первое называется видовым по отношению ко второму. Например, понятие “ромб” является родовым по отношению к понятию “квадрат”. Введение понятия через ближайший род и видовые заключается в следующем:
1)указывается род, в который входит определяемое понятие;
2)указываются видовые отличия и связь между ними.

Например, «Ромб - это параллелограмм, две смежные стороны которого равны». Родовым понятием выступает понятие параллелограмма, из которого определяемое понятие выделяется посредством одного видового отличия (равенство смежных сторон).

По отношению объемов различают следующие виды понятий: равнозначные, объемы которых полностью совпадают; пересекающиеся, объемы которых частично пересекаются; находящиеся в отношении включения, объем одного понятия содержится в объеме другого понятия.

к плану

4.4. ПУТИ ФОРМИРОВАНИЯ ПОНЯТИЙ.КЛАССИФИКАЦИЯ ПОНЯТИЙ

Формирование понятий – сложный психологический процесс. Он осуществляется и протекает по следующей схеме:

ощущения -> восприятие -> представление -> понятие

Процесс формирования понятий состоит из мотивации введения понятия, выделения его существенных свойств, усвоения определения, применения понятия, понимания связи изучаемого понятия с ранее изученными понятиями. Формирование понятия осуществляется в несколько этапов:

1. мотивация (подчеркивается важность изучения понятия, активизируется целенаправленная деятельность школьников, возбуждается интерес к изучению понятия с помощью привлечения средств нематематического содержания, выполнения специальных упражнений, объясняющих необходимость развития математической теории);

2. выявление существенных свойств понятия (выполнение упражнений, где выделяются существенные свойства изучаемого понятия);

3. формулировка определения понятия (выполнение действий на распознавание объектов, принадлежащих понятию, конструирование объектов, относящихся к объему понятия).

Выделяются два пути формирования понятий (рис. 6).

Рис.6. Пути формирования понятий

Объем понятия раскрывается с помощью классификации. Под классификацией часто понимают последовательное, многоступенчатое разбиение множества на классы с помощью некоторого свойства.

Классификация понятий - выяснение объема понятий, т.е. разделение множества объектов, составляющих объем родового понятия, на виды. Это разделение основано на сходстве объектов одного вида и отличии их от объектов других видов. Правильная классификация понятий предполагает соблюдение некоторых условий:

1. Классификация должна проводиться по определенному признаку, остающемуся неизменным в процессе классификации.

2. Понятия, получающиеся в результате классификации, должны быть взаимно независимыми, т.е. их пересечение должно быть пустым множеством.

3. Сумма объемов понятий, получающихся при классификации, должна равняться объему исходного понятия.

4. В процессе классификации необходимо переходить к ближайшему в данном родовом понятии виду.

Классификация натуральных чисел (рис. 7) и классификация треугольников по сторонам и углам (рис. 8), позволяют наблюдать выполнение этих четырех условий.

Рис. 7. Классификация натуральных чисел

Рис. 8. Классификация треугольников

методическом смысле полезными в обучении математике могут оказаться и схемы, на которых изображена зависимость изучаемых объектов. Например, в курсе планиметрии рассмотрим класс четурехугольников (рис. 9):

Рис. 9. Схема четурехугольников

к плану

4. 5. ОПРЕДЕЛЕНИЕ ПОНЯТИЯ. ВИДЫ ОПРЕДЕЛЕНИЙ

Заключительным этапом формирования понятия является его определение. Определить понятие - это значит перечислить его существенные свойства. Определение понятия - это предложение, в котором раскрывается содержание понятия, т. е. совокупность условий, необходимых и достаточных для выделения класса объектов, принадлежащих определяемому понятию.

Явные и неявные определения.

Явные и неявные определения различаются в зависимости от своей структуры. Явные определения содержат прямое указание на существенные признаки определяемого понятия; определяемое и определяюще в них выражено четко и однозначно. Например, «Углом называется фигура, образованная двумя лучами, выходящими из одной точки»; «Прямоугольник есть параллелограмм с прямым углом».

Явное определение объектов, обозначение выражений, дескрипция («Выражение a + a + ... + a (n слагаемых) ввиду его важности кратко обозначают na . Символ na обозначает сумму n слагаемых, каждое из которых равно a »).

Дескрипциями называются определения математических объектов путем указания их свойств (“То число, которое будучи умножено на длину диаметра, дает длину его окружности” - дескрипция числа p ).

Неявные определения объектов не содержат четкого и однозначного ределяющего элемента, в них содержание определяемого может быть установлено через некоторый контекст.

Номинальные и реальные определения.

Все определения, которые применяются в математике и других науках, делятся на номинальные и реальные, в зависимости от того, что определяется - знаковое выражение (термин, символ) или реальный объект, обозначаемый им . С помощью номинального определения вводится новый термин, символ или выражение как сокращения для более сложных выражений из ранее введенных терминов или символов, или уточняется значение уже введенного термина или символа. Номинальные определения являются средством обогащения языка науки и уточнения семантики его выражений (“Квадратным корнем из неотрицательного числа а называется такое неотрицательное число х , что х² = а”).

С помощью реальных определений фиксируются характеристические свойства самих определяемых объектов. Деление определений на номинальные и реальные не связано с их формальной структурой. Одно и то же определение можно представить и как номинальное, и как реальное. Например, пусть дано реальное определение: «Пятиугольник – есть плоская геометрическая фигура, ограниченая пятью сторонами». Это же определение можно переформулировать как номинальное: «Пятиугольником называется плоская геометрическая фигура, ограниченная пятью сторонами».

Контектуальные и индуктивные определения.

В математике начальных классов часто применяются контекстуальные определения, в которых определение нового неизвестного термина, понятия выясняется из смысла прочитанного, сводится к указанию содержащих его контекстов («больше», «меньше», «равно»).

Индуктивными называются определения, которые позволяют из сходных объектов (теории) путем применения к ним конкретных операций получать новые объекты. Например, по индукции вводит c я определение натурального числа в математике.

Аксиоматические определения.

Если определения исходных понятий даются посредством исходных понятий некоторой теории через ее аксиомы, то это аксиоматические определения . При аксиоматическом построении математической теории некоторые понятия остаются неопределенными (например, точка, плоскость и расстояние в аксиоматике А.Н. Колмогорова). Определением этих понятий можно считать систему аксиом, описывающих их свойства.

Определения через род и видовые отличия.

Классическими определениями называются определения через род и видовое отличие. Их можно рассматривать как частный вид номинальных определений. В них определяемое выделяется из предметов некоторой области, которая при этом явно упоминается в определении (род), путем указания характеристического свойства определяемого (видовое отличие). Например:

«Квадрат - прямоугольник с равными сторонами».

«Ромб - параллелограмм, у которого все стороны равны».

«Параллелограммом называется четырехугольник, противоположные стороны которого параллельны».

«Прямоугольник есть параллелограмм с прямым углом».

Общая схема определения “через ближайший род и видовое отличие” может быть записана на языке множеств (классов):

B = { x / x € A и P (x) }

(класс B состоит из объектов x, принадлежащих A - ближайшему роду и обладающих свойством P - видовое отличие) или на языке свойств:

x € B <=> x € A и P (x) , или B (x) <=> A (x) и P(x)

(объект x обладает свойством В тогда и только тогда, когда он обладает свойством А и свойством Р).

В школьном курсе математике определения через род и видовое отличие: Длина ломаной. Периметр многоугольника (прямоугольника, квадрата). Квадрат. Куб. Круг. Радиус окружности (круга). Биссектриса угла. Развернутый угол. Прямой угол. Градус. Острый угол. Тупой угол. Виды треугольников по величине углов. Фигуры, симметричные относительно точки (центр симметрии). Перпендикулярные и параллельные прямые.

Генетические определения.

Широкое распространение в школьном курсе математики получили генетические (конструктивные) определения, т.е. такие определения, в которых описывается или указывается способ его происхождения, образования, возникновения, построения. Генетические определения представляют собой разновидность определения через род и видовые отличия.

Например: «Сферой называется поверхность, полученная вращением полуокружности вокруг своего диаметра»; «Шар – это геометрическое тело, образованное вращением полуокружности вокруг диаметра».

Анализируя школьный курс математики, можно выделить следующие генетические определения понятий: Отрезок. Луч. Равносторонний треугольник. Координатный луч. Равные фигуры. Площадь прямоугольника. Площадь квадрата. Объем прямоугольного параллелепипеда. Окружность. Дуга окружности. Сектор. Угол и его элементы. Равные углы. Длина окружности. Площадь круга.

Определение через абстракцию.

Определения, связанные с выделением такого типа объектов через установление между ними отношений равенства, равнозначности, тождества, получили название определений через абстракцию . В таком определении данное математическое понятие определяется как семейство классов эквивалентности по некоторому отношению эквивалентности. Например, натуральное число n - это характеристика класса эквивалентных конечных множеств, состоящих из n элементов.

Остенсивные определения.

Остенсивные определения - определения значений слов путем непосредственного показа, демонстрации предметов. Часто применяются в начальной школе (понятия отрезка, окружности, угла и др.). Постепенно с развитием математического опыта и накоплением определенного числа понятий на смену остенсивным понятиям приходят вербальные понятия. Вербальные понятия – это понятия, когда значения неизвестных выражений определяются через выражения, значения которых известны.

Определение называется корректным , если выполняются два условия:

а) отсутствует порочный круг и связанная с ним возможность исключения нововведенных терминов (“Решение уравнения - это то число, которое является его решением”);
б) отсутствует омонимия: каждый термин встречается не более одного раза в качестве определяемого.

к плану

4.6. ТЕОРЕМА. ВИДЫ ТЕОРЕМ. МЕТОДИКА РАБОТЫ НАД ТЕОРЕМОЙ

Формой связи понятий друг с другом является суждение. Если суждения правильно отображают объективно существующие зависимости между вещами, то такие суждения называют истинными; в противном случае суждения будут ложными. Процесс получения нового суждения-вывода из одного или нескольких данных суждений называется умозаключением. Важнейшими видами сложных суждений являются теоремы и аксиомы (постулаты).

Аксиома (греч. - авторитетное предложение “то, что приемлемо”) - предложение, принимаемое без доказательства. Аксиомы и первичные (неопределяемые) понятия составляют основной фундамент математической теории.

К системе аксиом, характеризующих некоторую научную теорию, предъявляются требования независимости, непротиворечивости, полноты.

Постулат (лат. - требование) - предложение, в котором выражается некоторое требование (условие), которому должно удовлетворять некоторое понятие или некоторое отношение между понятиями.

При изучении свойств различных математических объектов приходится делать те или иные заключения, то есть на основе понятий и суждений того или иного раздела математики строить предложения, истинность которых необходимо обосновать.

Математическое предложение, истинность которого устанавливается посредством доказательства (рассуждения), называется теоремой.

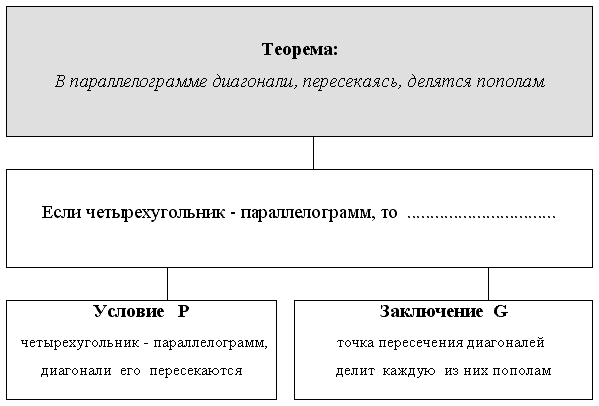
Существует два вида формулирования теоремы: условная, категорическая. Всегда можно из одного вида формулирования теоремы перейти в другому. Если теорема сформулирована в условной форме, то в ней должно быть ясно указано: при каких условиях рассматривается в ней тот или иной объект (условие теоремы) и что в этом объекте утверждается (заключение теоремы) (рис. 10).

Рис. 10. Структура теоремы

Доказательство теоремы состоит в том, чтобы показать, что если выполняется условие, то из него логически следует заключение, т. е., приняв, что P истинно, в соответствии с правилами вывода показать, что G истинно, и тем самым получить возможность утвердить, что данное высказывание (теорема) истинно в целом.

Доказательство включает в себя три основных элемента:

1. Тезис (главная цель доказательства - установить истинность тезиса). Форма выражения тезиса - суждение.

2. Аргументы (основания) доказательства - положения, на которые опирается доказательство и из которых при условии их истинности необходимо следует истинность доказываемого тезиса. Форма выражения аргументов - суждения. Связывая аргументы, приходим к умозаключению, которые строятся по определенным правилам. Аргументы, на которые можно опереться при доказательстве: аксиомы, определения, ранее доказанные теоремы.

3. Демонстрация - логический процесс взаимосвязи суждений, в результате которого осуществляется переход от аргументов к тезису.

Известно, что имея некоторую (прямую) теорему ( P => G ), можно образовать новые теоремы, и не одну:

G => P - обратная;
_ _
P => G - противоположная;
_ _
G => P - контрапозитивная (обратная противоположной или противоположнообратная).

Между этими четырьмя видами теорем существует тесная связь:
_ _
а) (P =>G) и (G => P) - одновременно истинны или ложны;
_ _
б) (G =>P) и (P => G) - одновременно истинны или ложны.

Изучая какую-либо теорему школьного курса математики, учитель должен придерживаться следующей последовательности:

Постановка вопроса (создание проблемной ситуации).
Обращение к опыту учащихся.
Высказывание предположения.
Поиск возможных путей решения.
Доказательство найденного факта.
Проведение доказательства в максимально простой форме.
Установление зависимости доказанной теоремы от ранее известных.

Процесс изучения школьниками теоремы включает следующие этапы: мотивация изучения теоремы; ознакомление с фактом, отраженным в теореме; формулировка теоремы и выяснение смысла каждого слова в формулировке теоремы; усвоение содержания теоремы; запоминание формулировки теоремы; ознакомление со способом доказательства; доказательство теоремы; применение теоремы; установление связей теоремы с ранее изученными теоремами.

к плану

4. 7. МЕТОДЫ ДОКАЗАТЕЛЬСТВА ТЕОРЕМ

Рассуждение с целью обоснования истинности какого-либо утверждения есть доказательство . Существуют различные методы доказательства теорем. Под методом доказательства будем понимать способ связи аргументов при переходе от условия к заключению суждения. Методы доказательства, используемые в школьном курсе математики, можно выделить по двум основаниям: по пути обоснования тезиса (прямое и косвенное); по математическому аппарату, используемому в доказательстве.

К прямым приемам доказательства относятся:

Прием преобразования условия суждения (синтетический).
Прием преобразования заключения суждения: а) отыскание достаточных оснований справедливости заключения (восходящий анализ); б) отыскание необходимых признаков справедливости суждения с последующей проверкой обратимости рассуждений (нисходящий анализ).
Прием последовательного преобразования то условия, то заключения суждения.

К косвенным приемам поиска доказательств относятся:

1. Метод “от противного” (истинность доказываемого тезиса устанавливается посредством опровержения противоречащего ему суждения).

2. Разделительный метод или метод разделения условий (тезис рассматривается как один из возможных вариантов предположений, когда все предположения отвергаются, кроме одного), иначе этот метод называют методом исключения.

К методам доказательства, выделенным по второму основанию, когда способ связи аргументов согласуется с определенной математической теорией в школьном курсе математики, относятся:

1. Метод геометрических преобразований. Э тот метод в школе используется как средство обоснования некоторых отношений между элементами евклидовой геометрии. Состоит он из выполнения последовательности шагов: выбирается геометрическое преобразование, обладающее свойством, которое позволяет обосновать наличие указанного отношения между объектами евклидовой геометрии; выполняется преобразование, при котором один объект переходит в другой; обосновывается наличие указанного отношения между объектами с помощью свойств выбранного геометрического преобразования.

2. Алгебраические методы (уравнений, неравенств, тождественных преобразований).

3. Векторный метод, использующий аппарат векторной алгебры.

4. Координатный метод , Координатный метод - это способ определения положения точки на прямой, на плоскости или в пространстве с помощью чисел (например, в декартовой системы координат ли какой-либо другой). Используя координатный метод, алгебраические уравнения можно истолковать в виде геометрических образов (графиков или фигур) и, наоборот, искать решение геометрических задач с помощью аналитических выражений (уравнений, неравенств или их систем).

При доказательстве математических утверждений используются разные математические методы.

Для того, чтобы учащиеся овладели прямым и косвенным доказательствами, необходимо сформировать у них определенную последовательность умений:

- умение искать доказательство,
- умение проводить доказательство,
- умение оформлять доказательство теоремы.

к плану

? Вопросы для самопроверки

Какова роль мышления в учебном процессе? Охарактеризуйте качества научного мышления. Что такое математическое мышление? Назовите основные мыслительные операции.
Что такое понятие? Охарактеризуйте главные логические характеристики понятия. Что значит «определить понятие»? Термин, род, вид, логическая связь. Что представляют собой компоненты понятия: существенные и несущественные свойства.
Каково соотношение между объемом и содержанием понятия?
Каковы способы определения понятий? Приведите примеры:
а) через ближайший род и видовое отличие;
б) генетический;
в) индуктивный;
г) абстрактный.
Охарактеризуйте методику введения понятий:
а) абстрактно-дедуктивным методом;
б) конкретно-индуктивным методом.
Какова роль определений в процессе усвоения понятий? Назовите виды определений и охарактеризуйте их.
Раскройте содержание этапов формирования математических понятий и проиллюстрируйте их на конкретных примерах.
Назовите структурные элементы теоремы. Формы теорем (категоричная и условная). Приведите примеры.
Какова взаимосвязь между прямой, обратной, противоположной, обратной противоположной теоремами.
Охарактеризуйте методы доказательства теорем.
Что представляют собой основные этапы работы над теоремой.
Дайте логико-математический анализ теоремы (по выбору).

к плану

Литература

Александрова Н.В. Математические термины. - М.: Высшая школа, 1978.
Болтянский В. Г. Использование логической символики при работе с определениями // Математика в школе. - 1973. - № 5.
Виленкин Н. Я., Абайдулин С. К., Товарткиладзе Р. К. Определения в школьном курсе математики и методика работы с ними // Математика в школе. - 1984. - № 4.
Войшвилло Е.К. Понятия как форма мышления. – М., 1989.
Гладкий А.В. Язык, математика и лингвистика // Математика в школе. - 1994. - № 1.
Груденов Я.И. Изучение определений, аксиом и теорем. - М.: Просвещение, 1981.
Дорофеев Г.В. Язык преподавания математики и математический язык // Современые проблемы методики преподавания математики. – М.: Просвещене, 1985.
Дразнин И.Е. О применении обратных и противоположных теорем в курсе геометрии // Математика в школе. - 1994. - № 6.
Дразнин И. Е. О работе над определениями // Математика в школе. - 1995. - № 5.
Колягин Ю.М. Основные понятия современного школьного курса математики. - М., 1974.
Курбатов В.И. Логика. Систематический курс. – Ростов н/Д: Феникс, 2001.
Мантуров О. В., Солнцев Ю. К. и др. Толковый словарь математических терминов. - М.: Просвещение, 1965.
Математика: Справочник школьника и студента / Франкл и др.; Пер. с нем. – М.: Дрофа, 1999.
Математика в понятиях, определениях и терминах / Мантуров О.В., Солнцев Ю.К., Сорокин Ю.И. и др. / Под ред. Л.В. Сабинина . - Ч. 1, 2. - М, 1987.
Никитин В.В., Рупасов К.А. Определения математических понятий в курсе средней школы. – М.: Просвещение, 1963.
Новосельцева З.И. Некоторые примеры мотивации изучения теорем // Математика в школе. - 1985. - № 5.
Петриченко О. Достаточно или необходимо / Математика: Приложение к 1 сентября. - № 23. - 1995.
Розин В. М. Семиотический анализ знаковых средств математики // Семиотика и восточные языки. - М., 1967.
Саранцев Г.И. Обучение матматическим доказательствам в школе. – М.: Просвещение, 2000.
Сойер У.У. Интуитивное понимание математического доказательства // Математика в школе. - 1991. - № 2.
Стратилатов П.В. О терминологии в школьном курсе геометрии // Математика в школе. - 1986. - № 2.
Талызина Н.Ф. Формирование математических понятий // Формирование приемов математического мышления / Под ред. Н.Ф.Талызиной. – М.: ТОО «Вентана-Граф», 1995.
Тимофеева И.Л. Некоторые замечания о методе доказательства от противного // Математика в школе. - 1994. - № 3.
Финкельштейн В. М. О подготовке учеников к изучению нового понятия, новой теоремы // Математика в школе. - 1996. - № 6.
Формирование приемов математического мышления / Под ред. Н. Ф. Талызиной. - М.: ТОО «Вентана-Граф», 1995.
Шумихин В.В., Немятышева С.В. Использование «разрезных» теорем на уроках геометрии // Математика в школе. - 1994. - № 3.