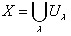
Если на евклидовой плоскости Е 2 задать прямоугольную декартову систему координат, то каждой точке плоскости будет соответствовать пара чисел ( х , у ) и обратно, каждой паре чисел - единственная точка на плоскости. Таким образом, задание системы координат порождает отображение f : Е 2 ® R 2 , которое является гомеоморфизмом. Это можно обобщить на случай произвольного топологического пространства.
Пусть (Х, τ ) - отделимое топологическое пространство.
Определение 25.1. n - мерной картой (или n -мерной системой координат) называется гомеоморфизм
φ : U ® R n некоторого открытого множества U Î τ на R n. При этом множество U называется координатной окрестностью карты . Если точка x Î U, то φ( х ) = ( х 1, х 2,..., х n) Î R n . Эти n действительных чисел называются координатами точки х в карте φ.
Определение 25.2. Связное, отделимое топологическое пространство (Х, τ ) со счетной базой называется n -мерным многообразием , если существует покрытие этого пространства координатными окрестностями n - мерных карт: 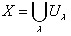
Из данного определения следует, что каждая точка многообразия имеет окрестность, гомеоморфную R n.
Пример 1. Числовое пространство R n связно, отделимо, имеет счетную базу. В качестве карты φ можно взять тождественное преобразование φ : R n ® R n. Координатная окрестность этой карты - все пространство R n. Значит, R n - n -мерное многообразие. Отсюда следует, что аффинное n -мерное пространство А n и евклидово E n являются многообразиями.
Пример 2. Рассмотрим обычную сферу S радиуса r в трехмерном евклидовом пространстве E 3 с центром в начале координат. Точки А (0, 0, r ) и В (0, 0, - r ) - полюсы сферы.
|
Рассмотрим два центральных проектирования: φ: S\{A} ® (XOY) из центра А и ψ: S\{B} ® (XOY) из центра В . Сфера S в индуцированной топологии является связным отделимым топологическим пространством со счетной базой. Множества S \{ A } и S \{ B } являются открытыми в этой топологии, а отображения φ и ψ - гомеоморфизмы. Следовательно, φ и ψ - две двумерных карты, причем их координатные окрестности образуют покрытие сферы. Следовательно, сфера является двумерным многообразием. |
Обозначим R n+ = {(x1, x2,..., xn) Î Rn | xn ≥ 0}. Это есть полупространство в R n вместе с границей.
Определение 25.3. Связное, отделимое топологическое пространство (Х, τ ) со счетной базой называется n -мерным многообразием с краем , если каждая его точка имеет окрестность, гомеоморфную R n или R n+.
Краем многообразия при этом называется множество тех точек пространства Х, которые имеют окрестность, гомеоморфную R n+, но не имеют окрестности, гомеоморфной R n .
Примеры. 1. Отрезок [ a , b ] на числовой прямой R является одномерным многообразием с краем. Край состоит из двух точек a и b .
2. Открытый круг на плоскости - двумерное многообразие без края. Замкнутый круг (круг вместе с ограничивающей его окружностью) на плоскости является двумерным многообразием с краем. Край - окружность.
3. Сфера - двумерное многообразие без края.
4. Открытый шар в пространстве - трехмерное многообразие без края. Замкнутый шар - трехмерное многообразие с краем. Край - сфера.
5. Окружность - одномерное многообразие без края.
6. Числовая прямая R - одномерное многообразие без края.
7. Полуплоскость у ≥ 0 - двумерное многообразие с краем. Край - ось абсцисс.