§22. Непрерывные отображения

Пусть даны два топологических пространства (Х, τ) и (Х′, τ′).

Определение 22.1. Отображение f : X ® Х′ называется непрерывным в точке х0 Î Х, если для любой окрестности V точки f (x0) существует окрестность U точки х0 , такая, что f (U ) V .

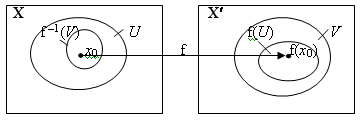
Переходя к прообразам, будем иметь: х0 Î U f -1 ( V ). Это означает, что f -1 ( V ) - окрестность точки х0 . Поэтому можно дать и другое определение непрерывности.

Определение 22.2. Отображение f : X ® Х′ называется непрерывным в точке х0 Î Х, если прообраз любой окрестности точки f(x0) является окрестностью точки х0 .

В топологии изучаются главным образом отображения f : X ® Х′ , которые непрерывны в каждой точке х Î Х. Такие отображения называются непрерывными отображениями пространства Х в пространство Х′ . Тривиальным примером непрерывного отображения служит тождественное отображение I : X ® X , при котором каждая точка преобразуется в себя.

Обратимся к тому частному случаю определения непрерывности в точке, когда пространства Х и Х′ являются метрическими. Тогда отображение f : (Х, ρ) ® (Х′ , ρ′ ) непрерывно в точке х0 , если " ε>0 $ δ>0 такое, что из неравенства ρ ( х0 , х ) < δ следует ρ′ ( f (х0), f (х)) < ε . Таким образом, в случае метрических пространств определение непрерывности в точке становится определением непрерывности обычной числовой функции " на языке ε - δ "

Теорема 22.1 . Отображение f : X ® Х′ непрерывно тогда и только тогда, когда прообраз любого открытого множества из Х′ является открытым множеством в Х.

Доказательство. I . Пусть отображение f : X ® Х′ непрерывно. Докажем, что прообраз любого открытого множества открыт. Пусть А′ Î τ′. Его прообраз f -1(A′ ). Выберем произвольную точку х Î f -1(A′ ). Тогда f (x) Î A′. Так как А′ Î τ′, то А′ - окрестность точки f (x). Отображение f - непрерывно, поэтому проообраз А′ f -1(A′ ) является окрестностью точки x . В силу произвольности выбора точки x получим, что множество f -1(A′ ) является окрестностью каждой своей точки, т.е. открыто.

II . Пусть " U ′ Î τ′, f -1 (U ′) Î τ (прообраз любого открытого множества открыт). Возьмем " х Î Х, f (x) Î Х′ и произвольную окрестность U ′f(x) точки f (x). По определению окрестности $ A′ Î τ′ | f (x) Î A′ U ′f(x). Переходя к прообразам, имеем: x Î f -1 (А′ ) f -1 (U ′f(x)). Но f -1 (А′ ) открыт по условию => f -1 (U ′f(x)) - окрестность точки х , т.е. прообраз окрестности f (x) является окрестностью x => f - непрерывно. Теорема доказана.