§21. Бикомпактные пространства  

Определение 21.1. Топологическое пространство (Х, τ) называется бикомпактным , если оно удовлетворяет аксиоме Бореля-Лебега: всякое его открытое покрытие содержит конечное подпокрытие.

Так антидискретное пространство всегда бикомпактно. Пространство с дискретной топологией бикомпактно тогда и только тогда, когда оно состоит из конечного множества точек.

Теорема 21. 1. Бесконечное множество, наделенное топологией Зарисского, является бикомпактным пространством.

Доказательство. Пусть S ={U_α} - произвольное открытое покрытие Х, состоящее из бесконечного числа элементов и пусть U_{α o} ≠ Х. Тогда F_{α o} = Х \ U_{α 0}состоит из конечного множества точек х₁, х₂,..., х_n . Так как {U_α} - покрытие, то найдутся элементы покрытия, такие, что х₁ Î U_{α 1}, х₂ Î U_{α 2},..., х_n Î U_{α n}. Добавим сюда U_{α 0}, тогда система U_{α 0}, U_{α 1},... , U_{α n} образует конечное подпокрытие покрытия {U_α} и, следовательно, Х бикомпактно. Теорема доказана.

Теорема 21.2 . Для бикомпактности пространства Х необходимо и достаточно, чтобы любое семейство его замкнутых подмножеств с пустым пересечением содержало конечное подсемейство с пустым пересечением.

Доказательство. I . Пусть Х - бикомпактно и пусть {F_α} - произвольное семейство его замкнутых подмножеств, такое, что _α F_α = Ø. Тогда семейство {U_α}, где U_α = X \ F_α , образует открытое покрытие Х. В силу бикомпактности, существует конечный набор { U_{α 1},..., U_{α n}}, образующий покрытие Х, и по формулам Де Моргана:

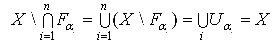
Следовательно, .

II . Пусть {U_α} - произвольное открытое покрытие Х. Рассмотрим семейство F_α = X \ U_α . Это семейство замкнутых в Х подмножеств с пустым пересечением, которое по условию содержит конечное подсемейство {F_{α 1}, F_α21,..., F_{α n}} такое, что . Ясно, что U_{α 1}, U_{α 2},... ..., U_{α n} образуют открытое покрытие Х. Теорема доказана.