 Х - некоторое непустое его подмножество. Рассмотрим семейство τА = {U A} подмножеств, каждое их которых есть пересечение с А всех подмножеств из τ . UA = U
Х - некоторое непустое его подмножество. Рассмотрим семейство τА = {U A} подмножеств, каждое их которых есть пересечение с А всех подмножеств из τ . UA = U 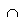 А, UÎτ . Легко проверить, что тогда семейство
А, UÎτ . Легко проверить, что тогда семейство
Топология любого пространства естественным образом задает (индуцирует) топологию на любом его подмножестве. В самом деле, пусть (Х, τ) - произвольное топологическое пространство, А  Х - некоторое непустое его подмножество. Рассмотрим семейство τА = {U A} подмножеств, каждое их которых есть пересечение с А всех подмножеств из τ . UA = U
Х - некоторое непустое его подмножество. Рассмотрим семейство τА = {U A} подмножеств, каждое их которых есть пересечение с А всех подмножеств из τ . UA = U 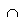 А, UÎτ . Легко проверить, что тогда семейство
А, UÎτ . Легко проверить, что тогда семейство
{UA} = τА удовлетворяет всем аксиомам топологии и (А, τА) - есть топологическое пространство, которое называется подпространством пространства Х. Топология τАпри этом называется индуцированной топологией.
|
Предположим теперь, что множество В , в свою очередь, является подмножеством А . Тогда на В индуцируются две топологии: одна, которая индуцируется из пространства (Х, τ), а вторая - из подпространства ( А, τА). Эти две топологии, как нетрудно убедиться, совпадают. Другими словами, индуцирование топологий транзитивно. Разумеется, без этого свойства понятие индуцированной топологии было бы некорректно. |
Пусть (А,τА) - подпространство пространства (Х, τ) и В - подмножество A: B A.
A.
Теорема 17.1 . Подмножество B (А,τА)
(А,τА)  (Х, τ) будет замкнутым в подпространстве (А, τА) тогда и только тогда, когда оно представляет собой пересечение с А некоторого замкнутого в Х множества:
(Х, τ) будет замкнутым в подпространстве (А, τА) тогда и только тогда, когда оно представляет собой пересечение с А некоторого замкнутого в Х множества:
В замкнуто в А <=> В = А
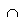 F, где F - замкнуто.
F, где F - замкнуто.
|
Доказательство. I . В замкнуто в А => СВ = А \ В открыто в А. Топология индуцирована из Х, поэтому А\В = А |
II . Пусть В= А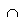 F, где F - замкнуто в Х => СF открыто в Х. СF = Х \ F Î τ. Но тогда (Х \ F)
F, где F - замкнуто в Х => СF открыто в Х. СF = Х \ F Î τ. Но тогда (Х \ F) 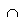 А открыто в А. (Х \ F)
А открыто в А. (Х \ F) 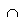 А Î τА, а его дополнение до А :
А Î τА, а его дополнение до А :
А \ [(Х \ F)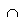 А] = B - замкнуто в А .
А] = B - замкнуто в А .
Теорема доказана.
В дальнейшем вместо выражения: "часть множества В , лежащая в А " будем говорить: "след В на А ". Итак, мы можем теперь сказать, что индуцированная из пространства Х топология в подмножестве А задается следами на А всех открытых, либо следами на А всех замкнутых множеств.
Пусть А - подпространство в Х и пусть В ![]() А , тогда очевидно, что если В открыто в Х, то В открыто и в А , ведь В
А , тогда очевидно, что если В открыто в Х, то В открыто и в А , ведь В 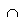 А = В и по определению подпространства В открыто в А . Что же касается обратного утверждения: "Если В открыто в А , то оно открыто в Х", то оно, вообще говоря, неверно. (Пример. В пространстве R3 любой круг без ограничивающей его окружности открыт в несущей его плоскости, однако не открыт, как подмножество R3 , ведь в нем нет ни одной внутренней точки). А для того, чтобы оно было верным, надо дополнительно потребовать, чтобы А само было открытым подмножеством в Х, тогда В будет открыто в Х, так как является пересечением открытых множеств: В = В
А = В и по определению подпространства В открыто в А . Что же касается обратного утверждения: "Если В открыто в А , то оно открыто в Х", то оно, вообще говоря, неверно. (Пример. В пространстве R3 любой круг без ограничивающей его окружности открыт в несущей его плоскости, однако не открыт, как подмножество R3 , ведь в нем нет ни одной внутренней точки). А для того, чтобы оно было верным, надо дополнительно потребовать, чтобы А само было открытым подмножеством в Х, тогда В будет открыто в Х, так как является пересечением открытых множеств: В = В 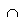 А.
А.
Совершенно аналогичная ситуация и с замкнутыми множествами: если В замкнуто в Х, то оно замкнуто и в А . Обратно, если В замкнуто в А , а А замкнуто в Х, то В замкнуто в Х.
Некоторое свойство пространства Х принято называть наследственным свойством, если этим свойством обладает каждое его подпространство. Например, открытость и замкнутость множества наследуются. Также свойство пространства удовлетворять первой или второй аксиоме счетности является свойством наследственным, ведь след счетной базы Х на любом подпространстве А  Х есть счетная база в А .
Х есть счетная база в А .