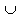§16. Линделефовы пространства  

Определение 16.1. Система S= {A_i, i Î I} множеств A_i Î(Х, τ) называется покрытием пространства Х, если 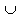_{i Î I} A_i = X.

Определение 16.2. Покрытие называется открытым (замкнутым) , если каждое из множеств A_i открыто (замкнуто) в Х.

Определение 16.3. Подсистема Т S покрытия S пространства Х называется подпокрытием покрытия S , если она сама образует покрытие Х.

Теорема 16.1 . (Линделефа). Если пространство Х обладает счетной базой, то из любого его открытого покрытия можно выделить не более, чем счетное подпокрытие.

Доказательство. Пусть β = {U_n} - некоторая счетная база пространства Х, а S= {G_i, iÎ I} - произвольное открытое покрытие Х. Для каждого х Î Х обозначим G_i(x) - один из элементов покрытия S , содержащий точку х . А по определению базы найдется элемент базы U_n(x)Î βтакой, что x Î U_n(x) G_i(x). Ясно, что объединение отобранного нами счетного числа множеств U_n(x)Î β совпадает со всем Х. Выбрав для каждого U_n(x) одно из содержащих его множеств G_i(x), мы получим не более, чем счетную систему, являющуюся подпокрытием покрытия S . Теорема доказана.

Пространства, удовлетворяющие данной теореме, образуют важный класс топологических пространств.

Определение 16.4. Топологическое пространство (Х, τ ) называется линделефовым или финально компактным , если из любого его открытого покрытия можно выделить не более чем счетное подпокрытие.