§14. База топологии  

Для задания во множестве Х топологии τ нет необходимости непосредственно указывать все открытые подмножества. Достаточно задать лишь некоторую совокупность открытых множеств, обладающую определенным свойством и называемую базой топологии.

Определение 14.1. Совокупность β τ открытых множеств пространства (Х, τ) называется базой топологии τ или базой пространства , если всякое открытое множество из τ является объединением открытых множеств из β.

Теорема 14.1 . Для того, чтобы совокупность открытых множеств β τ была базой топологии, необходимо и достаточно, чтобы для любой точки х и любой ее окрестности U ' x существовало открытое множество В Î β, такое, что хÎ ВU .

Доказательство. I . Пусть β - база пространства Х. Возьмем любую точку х и любую ее окрестность U' x. Тогда по определению окрестности $ V Î τ | x Î V U. А по определению базы V = 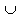_k B_k, В_k Î β. Но хÎ V, значит, он принадлежит хотя бы одному B_ko и x Î B_ko U.

II . Пусть для любой точки хÎ Х и любой ее окрестности U $ В_хÎ τ | xÎ B_x U . Нужно доказать, что В_хÎ β. Рассмотрим . Ясно, что В U, так как все В_х U. Обратно, если х Î U,
то х Î В_х U => хÎВ_х => х Î В => U В. Из В U & U В => U = В, т.е. - произвольное открытое множество представлено в виде объединения множеств В_х Î β. Поэтому β - база. Теорема доказана.

Понятно, что всякое пространство Х обладает базой, так как система всех открытых подмножеств подходит под определение базы. Из доказанной теоремы следуют также еще два свойства базы:

1. Объединение всех множеств, входящих в β , дает все множество Х.

Отсюда, в частности, следует, что изолированные точки пространства, если таковые имеются, непременно должны входить в любую базу этого пространства.

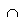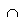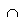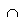2. Для любых двух множеств В₁ и В₂ из β и для каждой точки х Î В₁ В₂ $ В₃ Îβ | х Î В₃ В₁ В₂ (Это очевидно, так как В₁ Î τ, В₂ Î τ => В₁ В₂ Î τ и по теореме $ В₃ | хÎ В₃ В₁ В₂ )

Не всякая совокупность открытых множеств может служить базой некоторой топологии. Для того, чтобы система β открытых подмножеств была базой, необходимо, чтобы система обладала этими двумя свойствами.

Пример. Пусть β ^(-) - система всевозможных полуинтервалов ( а , b ] на прямой R . "хÎ(а, b] 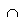(с, d]
$ (c, b] | хÎ(c, b] (а, b] 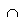(с, d] (свойство 2 базы). Очевидно, что " хÎ R принадлежит какому-либо полуинтервалу (а, b] (свойство 1 базы). Следовательно, система β ^(-) образует базу топологии полуоткрытых слева интервалов.