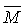 => М =
=> М = Теорема 11.1 . Множество М в топологическом пространстве (Х, τ) замкнуто тогда и только тогда, когда оно совпадает со своим замыканием.
Доказательство. I . Пусть М - замкнуто, => CМ Î τ,
СМ = Int (СМ) => по формуле (9.1): СМ = С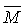 => М =
=> М = ![]() .
.
II . Пусть М = 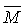 . Тогда СМ = С
. Тогда СМ = С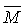 => по формуле (9.1): СМ = Int (СМ) => СМ Î τ => М - замкнуто. Теорема доказана.
=> по формуле (9.1): СМ = Int (СМ) => СМ Î τ => М - замкнуто. Теорема доказана.
Оказывается, что замыкание ![]() любого множества М представляет собой наименьшее замкнутое множество, содержащее исходное множество М, а именно, имеет место
любого множества М представляет собой наименьшее замкнутое множество, содержащее исходное множество М, а именно, имеет место
Теорема 11.2. Замыкание любого множества М пространства Х совпадает с пересечением всех замкнутых множеств, содержащих М .
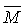 =
= 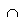 i Î I Fi, M
i Î I Fi, M  Fi " i Î I, Fi- замкнуты .
Fi " i Î I, Fi- замкнуты .
Доказательство. Пусть М - произвольное множество в топологическом пространстве Х
и пусть N = 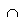 i Î I Fi,
М
i Î I Fi,
М Fi " i Î I. Заметим, что пересечение здесь распространено на все замкнутые множества, содержащие множество М, в частности,
Fi " i Î I. Заметим, что пересечение здесь распространено на все замкнутые множества, содержащие множество М, в частности, ![]() туда тоже входит, ибо М
туда тоже входит, ибо М 
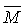 . Так как N - пересечение, то N
. Так как N - пересечение, то N  Fi , в том числе и N
Fi , в том числе и N 
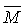 . Чтобы доказать обратное включение, возьмем любое замкнутое множество Fi, содержащее М: М
. Чтобы доказать обратное включение, возьмем любое замкнутое множество Fi, содержащее М: М  Fi.
По свойству монотонности замыкания
Fi.
По свойству монотонности замыкания 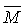

![]() , но
, но ![]() = Fi, так как Fiзамкнуто. Итак,
= Fi, так как Fiзамкнуто. Итак, 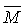
 Fi, а раз оно входит во все Fi , то входит и в их пересечение:
Fi, а раз оно входит во все Fi , то входит и в их пересечение: 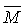
 N. Мы получили
N. Мы получили 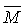 = N. Теорема доказана.
= N. Теорема доказана.
Теорема 11.3. Для любых двух множеств М и N топологического пространства (Х, τ) замыкание объединения равно объединению замыканий: ![]() .
.
Доказательство. Из включений M  M
M 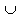 N, N
N, N  M
M 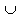 N в силу монотонности замыкания:
N в силу монотонности замыкания: 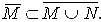 ,
, 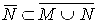 откуда следует:
откуда следует: 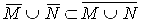 (*). Докажем обратное включение. Из М
(*). Докажем обратное включение. Из М 
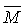 , N
, N 
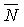 следует M
следует M 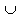 N
N 
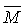
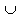
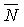 и по монотонности замыкания
и по монотонности замыкания ![]() (**). (Последнее равенство следует из того, что замыкание замкнутого множества есть оно само). Наконец, из (*) и (**) следует:
(**). (Последнее равенство следует из того, что замыкание замкнутого множества есть оно само). Наконец, из (*) и (**) следует: ![]() , что и требовалось.
, что и требовалось.