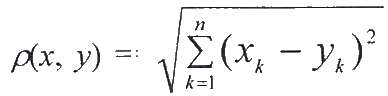 .
.Пусть Х - произвольное непустое множество, а ρ : Х × Х ® R + - отображение декартового квадрата этого множество во множество R + неотрицательных вещественных чисел.
Определение 1.1. Отображение ρ: Х × Х ® R + называется метрикой на Х, если оно удовлетворяет следующим трем условиям, называемым аксиомами метрики:
1*. ρ(х, у) = 0 <=> х = у (аксиома тождества);
2*. ρ(х, у) = ρ(y, x) " х, у Î Х (аксиома симметрии);
3*. ρ(х, у) ≤ ρ(х, z) + ρ(z, у) " х, у, z Î Х (аксиома треугольника).
Множество Х, рассматриваемое вместе с заданной на ней метрикой ρ, называется метрическим пространством . Элементы множества X называются при этом точками этого метрического пространства, а число ρ(х, у) - расстоянием между точками x и y .
На одном и том же множестве можно задать различные метрики, поэтому, чтобы их различать, метрическое пространство обозначают в виде пары ( X , ρ).
Числовая прямая.
Пусть R - множество вещественных чисел. Метрику зададим так: ρ(х, у) = | x - y |. Все аксиомы 1*- 3* выполняются. Полученное метрическое пространство ( R , ρ) называется числовой прямой R ..
Многомерное числовое пространство.
Пусть X - множество упорядоченных n -наборов действительных чисел x = ( x 1, x 2,..., x n ). Расстояние между элементами x = ( x 1, x 2,..., x n) и y = ( y 1, y 2,..., y n) зададим формулой
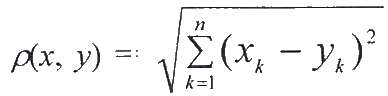 .
.
Полученное метрическое пространство ( R n , ρ) называется n -мерным числовым пространством или евклидовым пространством.
В том же множестве R n можно задать метрику ρ 0 по формуле ρ 0 (х, у) = max | x k - y k |. ( R n , ρ 0 ) - также n -мерное числовое пространство.
Дискретное метрическое пространство.
Пусть X - произвольное непустое множество. Полагая
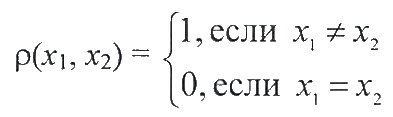 ,
,
мы увидим, что все аксиомы 1*-3* выполняются. Эта метрика называется дискретной метрикой, а пространство ( X , ρ) - дискретным метрическим пространством.
Пространство непрерывных функций C [ a , b ] .
Пусть X - совокупность вещественных функций, определенных и непрерывных на отрезке [ a , b ]. Метрику на данном множестве зададим следующим образом:
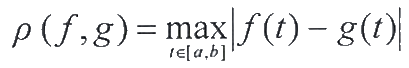 .
.
Полученное метрическое пространство ( X , ρ) обозначается C [ a , b ] и называется пространством непрерывных функций.