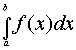Формулы Ньютона-Котеса. Погрешность квадратурных формул.

Можно продолжить процедуру построения квадратурных формул на равномерной сетке, используя на частичных отрезках интерполяционные полиномы более высоких степеней. Рассмотрим общий случай. Возьмем m+1 точку на отрезке [x_i-1, x_i] и построим интерполяционный полином Лагранжа степени m, совпадающий со значениями функции y=f(x) в этих точках. Интегрируя этот полином от x_i-1 до x_i и суммируя такие интегралы по отрезку [a,b] получим для каждого значения m соответствующую квадратурную формулу для вычисления интеграла .

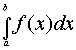Определение 4.5 Такие квадратурные формулы называются формулами Ньютона - Котеса.

Используя определение (4.5) можно показать, что составные квадратурные формулы Ньютона-Котеса имеют вид:

LN[f] = ∑Ni=1 li[f]	(4.23)

где

li[f] = h∑mj=0 cj f(ξij)	(4.24)

ξ_ij - точки из частичного отрезка [x_i-1, x_i], c_j - некоторые числовые коэффициенты, i=1, ..., N, j=0, ..., m. В частности:

1) для формулы прямоугольников: m=0, c₀=1, ξ_i0=(x_i-1+x_i)/2;

2) для формулы трапеций: m=1, c₀=c₁=1/2, ξ_i0=x_i-1, ξ_i1=x_i;

3) для формулы Симпсона: m=2, c₀=c₂=1/6, c₁=2/3, ξ_i0=x_i-1,

ξ_i1=(x_i-1+x_i)/2, ξ_i2=x_i.

Определение 4.6 Квадратурная формула L_N[f] называется точной для полинома степени r, если для любого полинома P(x) степени не выше r, для любого отрезка [a, b] и для любого числа N справедливо равенство:

УТВЕРЖДЕНИЕ 4.1 Квадратурные формулы прямоугольников, трапеций и Симпсона точны соответственно для полиномов нулевой, первой и второй степени.

ДОКАЗАТЕЛЬСТВО: Очевидно, так как интерполяционный полином степени r для функции, самой являющейся полиномом степени r, совпадает с этой функцией в силу теоремы единственности интерполяционного полинома.

Имеет место более сильное утверждение.

УТВЕРЖДЕНИЕ 4.2 Квадратурная формула прямоугольников точна для полиномов первой степени. Квадратурная формула Симпсона точна для полиномов третьей степени.

ЗАДАЧА 4.5 Доказать утверждение 4.2.

Порядок погрешности квадратурных формул оказывается связанным со степенью полиномов, относительно которых точна рассматриваемая квадратурная формула. Эта связь дается следующей теоремой.

ТЕОРЕМА 4.2 (о погрешности) Пусть y=f(x) является r ≥ 1 раз непрерывно дифференцируемой на отрезке [a, b] функцией и константа M > 0 такова, что |f^(r)(x)| ≤ M x [a, b].

Если квадратурная формула L_N[f] точна для полиномов степени r-1, то существует константа c_r > 0 не зависящая от f(x), такая что

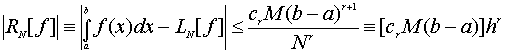	(4.25)

ДОКАЗАТЕЛЬСТВО: Рассмотрим i-тый частичный отрезок [x_i-1, x_i] и произвольную точку x на нем. Из курса математического анализа известно, что для функций из класса C^r справедливо разложение Тейлора f(x)=P_r-1,i(x)+Z_i(x), где

Pr-1,i = ∑j=0r-1f (j) (xi-1 )(x - xi-1 ) j/j!	(4.26)

полином Тейлора степени r-1;

Zi(x) = f(r) (ξ) (x - xi-1)r / r! -	(4.27)

остаточный член в форме Лагранжа, ξ(x_i-1,x). Тогда:

.

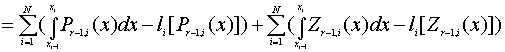Так как по условию квадратурная формула L_N[f] точна для полиномов степени r-1, то

.

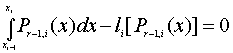Следовательно

	(4.28)

Из (4.27) и условий теоремы имеем:

|Zi(x)| ≤ Mhr/r!	(4.29)

Следовательно,

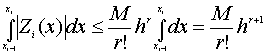	(4.30)

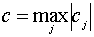Пусть , где величины c_j взяты из представления (4.24). Тогда в силу неравенства треугольника, оценки (4.29) и того, что ∑^m_j=0c_j ≤ c(m+1), получаем:

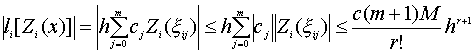	(4.31)

Обозначим c_r=(1+(m+1)c)/r! и подставим в (4.28) последние два неравенства (4.30) и (4.31), откуда получим требуемую оценку погрешности

Для конкретных квадратурных формул можно получить более точные, чем в доказательстве теоремы, выражения для констант c_r. Для трех рассмотренных выше формул наиболее точные значения этих констант дает следующее

УТВЕРЖДЕНИЕ 4.3 Для формулы прямоугольников c₂=1/24, для формулы трапеций c₂=1/12, для формулы Симпсона c₄=1/2880.

ЗАДАЧА^* 4.6 Доказать утверждение 4.3.

ЗАМЕЧАНИЕ 4.2 В качестве константы M в условии теоремы можно, очевидно, взять величину 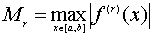или ее оценку сверху.