(xi,f(xi )) Таким образом вместо интеграла
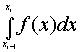 рассмотрим
величину
рассмотрим
величину
Заменим площадь криволинейной трапеции, образованной подграфиком функции y=f(x) на частичном отрезке [xi-1,xi], площадью другой криволинейной трапеции, образованной подграфиком функции y=P2,i(x), где
есть интерполяционный полином второй степени (парабола) в форме Лагранжа,
построенный по трем точкам
(xi-1,f(xi-1 )), (ξi,f(ξi )),
(xi,f(xi ))
Таким образом
вместо интеграла 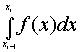 рассмотрим
величину
рассмотрим
величину
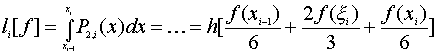 |
(4.20) |
|---|
ЗАДАЧА 4.3 Провести полный вывод формул (4.20) (Совет: при интегрировании воспользоваться заменами переменных вида: y= x-xi ).
В результате суммирования величин (4.20) по всему отрезку [a,b] получим квадратурную формулу Симпсона (формулу парабол):
| LN[f] = ∑Ni=1 li[f] = h ∑Ni=1 [f(xi-1 )/6 + 2f(ξi )/3 + f(xi )/6] | (4.21) |
|---|
Выпишем более удобное для численной реализации представление формулы Симпсона, очевидным образом полученное из предыдущего:
| LN[f] = h [f(a) + f(b) + 2∑i=1N-1 f(xi ) + 4∑i=1N f((xi-1 + xi )/2 )]\6 | (4.22) |
|---|
ЗАДАЧА 4.4 Показать эквивалентность представлений (4.21) и (4.22).