Формула прямоугольников.
Заменим на отрезке [xi-1, xi] функцию y=f(x)
полиномом нулевой степени, то есть константой.
Данный полином
можно однозначно провести через одну точку.
В качестве такой точки выберем
точку
(ξi, f(ξi)), где
ξi = (xi+xi-1 ) /2 - середина отрезка [xi-1 , xi].
Тогда полином, очевидно, имеет вид: P0,i(x)=f(ξi )
Здесь и далее первым нижним индексом будем обозначать степень полинома,
а вторым нижним индексом будем обозначать номер отрезка.
Теперь площадь
криволинейной трапеции, образованной подграфиком функции
y=f(x) на отрезке [xi-1,xi], заменим на площадь
прямоугольника с основанием [xi-1,xi] и высотой f(ξi),
то есть вместо 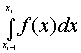 рассмотрим
рассмотрим
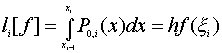 .
.
Суммируя площади всех таких прямоугольников на отрезке [a,b], получим:
LN[f] =
∑Ni=1
lN , i[f] =
h ∑Ni=1 f(ξi )
.
Вспоминая определение xi
окончательно получаем квадратурную
формулу (средних) прямоугольников:
| LN[f] =
h ∑Ni=1 f((xi-1 + xi )/2)
|
(4.17) |
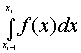 рассмотрим
рассмотрим
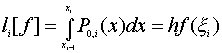 .
.