Постановка задачи численного интегрирования.
В курсе математического анализа изучаются методы вычисления различных
определенных интегралов. Например:
∫0π sin(x)dx = -cos(x) |0π = -(-1-1) = 2
Теперь попробуем вычислить каким-либо методом математического анализа
аналогичный интеграл вида
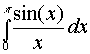 и убедимся в том, что он аналитически не вычисляется. Однако
практические задачи в своем большинстве приводят именно к такого типа
интегралам.
Как решается эта проблема?
В этих случаях применяется численное интегрирование.
Кроме того, если функция y=f(x) задана таблично, то приближенное
вычисление интеграла также выполняется численно.
и убедимся в том, что он аналитически не вычисляется. Однако
практические задачи в своем большинстве приводят именно к такого типа
интегралам.
Как решается эта проблема?
В этих случаях применяется численное интегрирование.
Кроме того, если функция y=f(x) задана таблично, то приближенное
вычисление интеграла также выполняется численно.
Прежде чем переходить к численным методам подсчета интегралов,
вспомним, как вводится интеграл Римана в курсе
математического анализа.
Проводится разбиение отрезка [a, b] на N частичных отрезков
[xi-1, xi], i = 1, ..., N, внутри каждого из которых выбирается
произвольная точка ξi. Далее составляется интегральная сумма:
SN=∑Ni=1 f(ξi ) (xi - xi-1 )
Тогда интеграл Римана определяется как следующий предел интегральных
сумм:
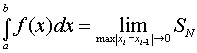
Если зафиксировать число N и не переходить к пределу, то
получим некоторое приближенное значение интеграла. Простейшие численные методы
нахождения значения интеграла основаны на подобных соображениях.
Задача численного интегрирования состоит в нахождении
приближенного значения интеграла:
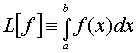 |
(4.15) |
где y=f(x) - заданная функция.
Введем на отрезке [a,b] сетку 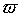 :
:
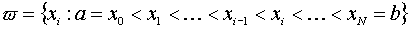
Точки xi называют узлами сетки (i=1, ..., N),
отрезки [xi-1,xi] - частичными отрезками,
числа hi=xi-xi-1 называют шагами сетки (i=1, ..., N).
В качестве приближенного значения интеграла L[f]
рассмотрим следующее:
|
LN[f] ≡∑
Ni=1
lN , i[f]
| (4.16) |
где li[f] - формула для приближенного вычисления интеграла
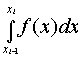 на частичном отрезке [xi-1,xi].
на частичном отрезке [xi-1,xi].
Определение 4.1
Формула li[f] называется простейшей квадратурной формулой.
Определение 4.2
Формула LN[f]
называется составной квадратурной формулой.
Определение 4.3
Разность L[f] - LN[f] ≡ RN[f]
называется погрешностью квадратурной формулы.
Определение 4.4
Если имеет место оценка |RN[f]| ≤ chp, где константа c > 0
не зависит от величины 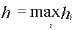 ,
то говорят, что погрешность квадратурной формулы
имеет порядок p.
,
то говорят, что погрешность квадратурной формулы
имеет порядок p.
В дальнейшем ограничимся равномерной сеткой, когда все шаги hi
одинаковы, то есть
hi=
h≡(a-b)/N, i=1, ..., N.
Квадратурные формулы, которые мы будем рассматривать, получаются
посредством замены функции y=f(x) на каждом частичном отрезке
[xi-1,xi] интерполяционными полиномами степени 0, 1 или 2.
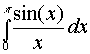 и убедимся в том, что он аналитически не вычисляется. Однако
практические задачи в своем большинстве приводят именно к такого типа
интегралам.
Как решается эта проблема?
В этих случаях применяется численное интегрирование.
Кроме того, если функция y=f(x) задана таблично, то приближенное
вычисление интеграла также выполняется численно.
и убедимся в том, что он аналитически не вычисляется. Однако
практические задачи в своем большинстве приводят именно к такого типа
интегралам.
Как решается эта проблема?
В этих случаях применяется численное интегрирование.
Кроме того, если функция y=f(x) задана таблично, то приближенное
вычисление интеграла также выполняется численно.
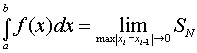
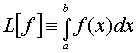
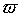 :
:
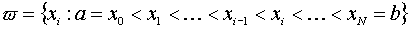
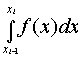 на частичном отрезке [xi-1,xi].
на частичном отрезке [xi-1,xi].
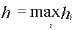 ,
то говорят, что погрешность квадратурной формулы
имеет порядок p.
,
то говорят, что погрешность квадратурной формулы
имеет порядок p.