(hi=xi - xi-1) в остаточный член,
называется порядком погрешности формулы
численного дифференцирования.
Формулы с отброшенными остаточными членами называются
просто формулами численного дифференцирования.
Допустим, что в некоторой точке x у функции f(x) существует производная r-того порядка f(r)(x) которую точно вычислить либо не удается, либо слишком сложно. В этом случае для приближенного нахождения производных функции используются формулы численного дифференцирования.
Задача численного дифференцирования состоит в приближенном вычислении производных функции f(x) по заданным в конечном числе точек значениям этой функции.
Один из универсальных способов построения формул численного дифференцирования состоит в том, что по значениям функции f(x) в некоторых узлах x0 , x1 , ... , xN строят интерполяционный полином PN(x) (обычно в форме Лагранжа) и приближенно полагают
| f (r)(x) ≈P(r)N(x), 0 ≤ r ≤ N | (4.1) |
|---|
В ряде случаев наряду с приближенным равенством удается (например, используя формулу Тейлора) получить точное равенство, содержащее остаточный член R (погрешность численного дифференцирования):
f (r)(x) = P(r)N(x) + R, 0 ≤ r ≤ N
Такие формулы называются формулами численного дифференцирования с
остаточными членами.
Степень, с которой входит величина
(hi=xi - xi-1) в остаточный член,
называется порядком погрешности формулы
численного дифференцирования.
Формулы с отброшенными остаточными членами называются
просто формулами численного дифференцирования.
Ниже приводятся несколько распространенных формул численного дифференцирования с остаточными членами для первой (r=1) и второй (r=2) производных в узлах, расположенных с постоянным шагом hi≡h > 0 [6, стр.58]:
r=1, N=1 (два узла):
| f '(x0 ) = (f1 - f0 )/h - hf ''(ξ)/2 | (4.2) |
|---|
| f '(x1 ) = (f1 - f0 )/h + hf ''(ξ)/2 | (4.3) |
|---|
r=1, N=2 (три узла):
| f '(x0 ) = (-3f0 + 4f1 - f2)/2h + h2f '''(ξ)/3 | (4.4) |
|---|
| f '(x1 ) = (f2 - f0)/2h - h2f '''(ξ)/6 | (4.5) |
|---|
| f '(x2 ) = (f0 - 4f1 + 3f2)/2h + h2f '''(ξ)/3 | (4.6) |
|---|
r=2, N=2 (три узла):
| f ''(x0 ) = (f0 - 2f1 + f2 )/h2 - hf '''(ξ) | (4.7) |
|---|
| f ''(x1 ) = (f0 - 2f1 + f2 )/h2 - h2f (4)(ξ)/12 | (4.8) |
|---|
| f ''(x2 ) = (f0 - 2f1 + f2 )/h2 + hf '''(ξ) | (4.9) |
|---|
r=2, N=3 (четыре узла):
| f ''(x0 ) = (2f0 - 5f1 + 4f2 - f3 )/h2 + 11h2f (4)(ξ)/12 | (4.10) |
|---|
| f ''(x1 ) = (f0 - 2f1 + f2 )/h2 - h2f (4)(ξ)/12 | (4.11) |
|---|
| f ''(x2 ) = (f0 - 2f1 + f3 )/h2 - h2f (4)(ξ)/12 | (4.12) |
|---|
| f ''(x3 ) = (-f0 + 4f1 - 5f2 + 2f3 )/h2 + 11h2f (4)(ξ)/12 | (4.13) |
|---|
В приведенных формулах ξ есть некоторая точка (своя для каждой из формул) из интервала (x0 , xN). Остаточные члены этих формул находятся с помощью формулы Тейлора. При этом предполагается, что на отрезке [x0 , xN] у функции f(x) непрерывна производная, через которую выражается остаточный член. При четном N в среднем узле для четной производной порядок точности формулы на единицу больше, чем в остальных узлах. Поэтому рекомендуется по возможности использовать формулы численного дифференцирования с узлами, расположенными симметрично относительно той точки, в которой ищется производная.
ЗАДАЧА 4.1 Вывести формулы (4.2)-(4.13).
Оценка погрешности общей формулы численного дифференцирования (4.1) выражается в виде неравенства через максимум модуля производной f(k+1)(x) при любых r, k, N, таких, что 0 ≤ r ≤ k ≤ N. Ограничиваясь рассмотрением случая расположения узлов с постоянным шагом h, сформулируем результат в виде теоремы (без доказательства).
ТЕОРЕМА 4.1 [6, стр.61]
Пусть xi=x0 + ih, h>0, i=0, ..., N
и функция f(x)
Ck+1[x0,xN].
Тогда существуют такие константы crkN,
зависящие только от r, k, N и
не зависящие от шага h и функции f(x), что
 |
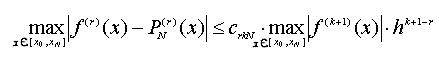(4.14) |
|---|
Оценка (4.14) полезна тем, что она устанавливает скорость убывания погрешности относительно h на всем отрезке [x0 , xN] при фиксированных параметрах r, k, N.
В формулах численного дифференцирования с постоянным шагом h значения функции f(x) делятся на hr, где r-порядок вычисляемой производной. Поэтому при малом h неустранимые погрешности в значениях функции f(x) оказывают сильное влияние на результат численного дифференцирования. Таким образом, возникает задача выбора оптимального шага h, так как погрешность собственно метода стремится к нулю при h → 0, а неустранимая погрешность растет. В результате общая погрешность, возникающая при численном дифферецировании, может неограниченно возрастать при h → 0. Поэтому операцию численного дифференцирования называют некорректной.
ЗАМЕЧАНИЕ 4.1 Другим способом нахождения производной табличной функции является использование формулы производной интерполяционного кубического сплайна, построенного по этой таблице. В этом случае производная вычисляется на каждом отрезке [xi-1 , xi], i=1, ..., N, по формуле (3.10), с использованием вектора (m0 ,..., mN )T, найденного методом прогонки как решение системы уравнений (3.13).