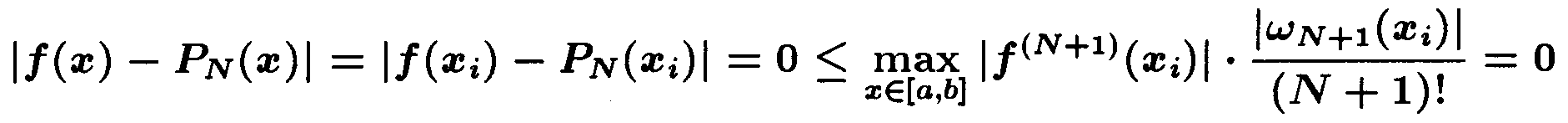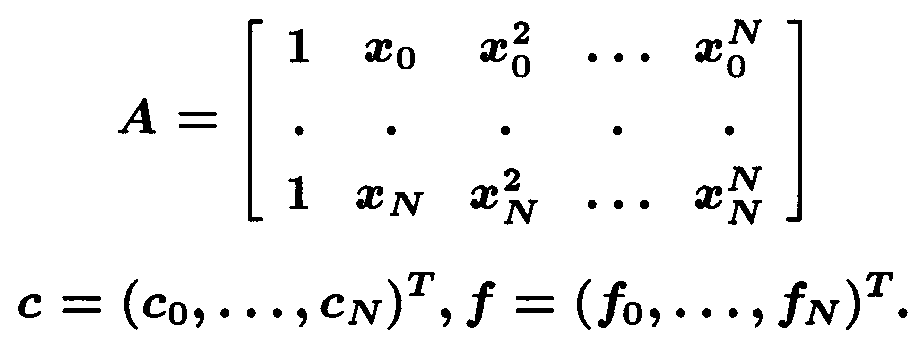
Интерполяционный полином.

Теорема существования и единственности.

ТЕОРЕМА 3.1 Для табличной функции 3.1 существует единственная интерполянта - полином степени не выше N.

ДОКАЗАТЕЛЬСТВО: Будем искать интерполянту F(x) в виде полинома:

P_N(x) = c₀ + c₁ x¹ + ... + c_N-1 x^N-1 + c_N x^N,

где c_i искомые коэффициенты. Используя таблицу (3.1) получим систему линейных уравнений:

c0 + c1 x0 + ... + cN x0N = PN (x0 ) = f0 ... c0 + c1 xN + ... + cN xNN = PN (xN ) = fN	(3.3)

В матричном представлении система имеет вид: Ac = f, где

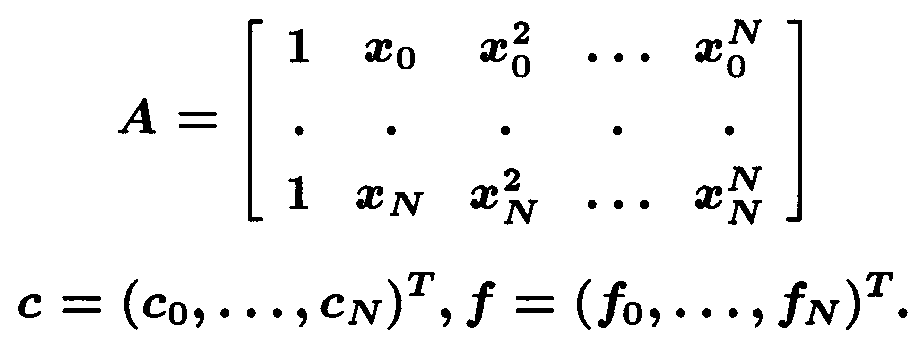
Известно, что система Ac=f однозначно разрешима тогда и только тогда, когда det(A)≠0 Определителем матрицы A является известный из курса алгебры определитель Ван-дер-Монда 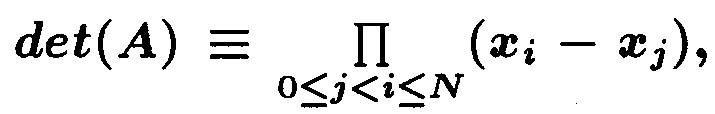не равный нулю в силу условия x_i≠x_j при i≠j. Таким образом, коэффициенты c₀ , ..., c_N (то есть решение c системы (3.3)) находятся однозначно. Следовательно, интерполяционный полином существует и единствен.

Данная теорема дает один из возможных способов построения интерполяционного полинома. Но для этого требуется решить другую сложную задачу - систему линейных уравнений. Существуют более простые способы построения интерполяционного полинома, которые будут рассмотрены далее.

Интерполяционный полином в форме Лагранжа.

УТВЕРЖДЕНИЕ 3.1 Имеют место следующие равенства

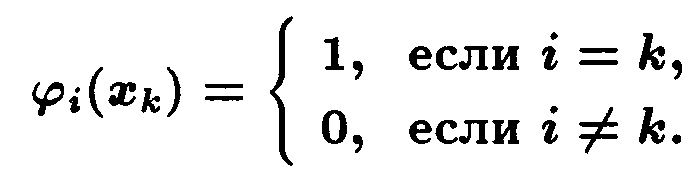
ДОКАЗАТЕЛЬСТВО следует сразу из определения базисных полиномов Лагранжа:

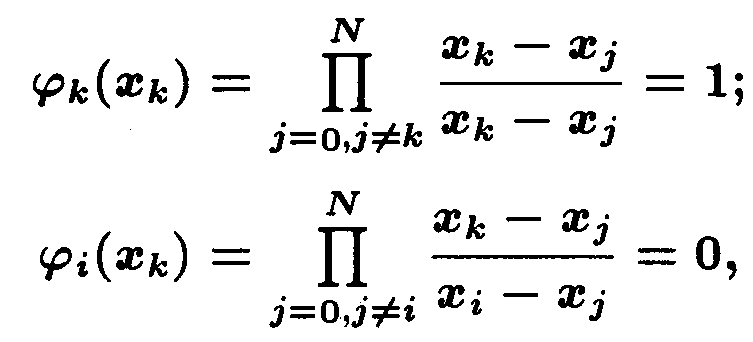
так как сомножитель (x_k - x_j )/(x_i-x_j ) равен нулю при j=k≠i (он присутствует в силу того, что i≠k)

Интерполяционный полином в форме Лагранжа имеет вид:

PN(x) = ∑Nj=0 fjφj(x) = f0φ0(x) + f1φ1(x) + ... + fNφN(x)	(3.4)

УТВЕРЖДЕНИЕ 3.2 P_N(x_i ) = f_i , i=0, ..., N, то есть полином P_N(x) является интерполяционным.

ДОКАЗАТЕЛЬСТВО следует из утверждения (3.1), так как

P_N(x_i ) = ∑^N_j=0 f_jφ_j(x_i ) = f_i·1 = f_i

Интерполяционный полином в форме Лагранжа обычно применяется в теоретических исследованиях (при доказательстве теорем, аналитическом решении задач и т. п.)

Интерполяционный полином в форме Ньютона.

Интерполяционный полином в форме Ньютона записывается в виде:

P_N(x) = c₀ + c₁ (x - x₀ ) + c₂ (x - x₀ )(x - x₁ ) + ... +
+ c_N (x - x₀ )(x - x₁ )· ... ·(x - x_N-1 )

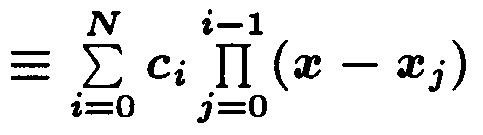
где коэффициенты c_i находятся из условий (3.1):

f₀=P_N(x₀ )=c₀. Cледовательно, c₀=f₀;

...

f_i=P_N(x_i )=c₀ + c₁(x_i - x₀ ) + ... + c_i-1(x_i - x₀ )(x_i - x₁ )...(x_i - x_i-2 ) +

+c_i(x_i - x₀ )(x_i - x₁ )...(x_i - x_i-1 ).

Следовательно,

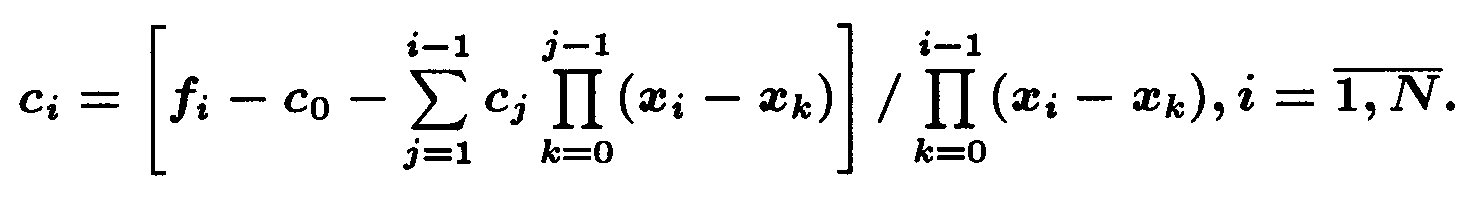
ЗАМЕЧАНИЕ 3.2 На практике чаще c_i находят через разделенные разности [стр.29-31].

ЗАМЕЧАНИЕ 3.3 В силу теоремы единственности интерполяционного полинома полиномы Ньютона и Лагранжа совпадают: P_N^Л(x) ≡P_N^Н(x).

ЗАМЕЧАНИЕ 3.4 Полином Ньютона обычно применяется в практических вычислениях на ЭВМ.

ЗАМЕЧАНИЕ 3.5 После того как вычислены коэффициенты c_i значение полинома Ньютона на ЭВМ следует подсчитывать по следующей формуле (схеме Горнера), удобной для программирования:

PN(x) = c0 + (x - x0 )[c1 + (x - x1 )[c2 + ... +(x - xN-1 )[cN-2 + (x - xN-1 )cN]...]	(3.6)

ЗАМЕЧАНИЕ 3.6 Из формул интерполяционных полиномов Лагранжа и Ньютона видно, что добавление новой точки (x_N+1 , f_N+1 ) к табличной функции потребует полного пересчета формул полинома Лагранжа и добавления лишь одного нового слагаемого, содержащего значение c_N+1 в формуле полинома Ньютона.

Погрешность при интерполяции полиномами.

ТЕОРЕМА 3.2 Пусть P_N+1(x) интерполяционный полином для таблицы 3.1 и f(x)C^N+1 [a,b], тогда

|R(x)| ≡ |f(x) - P_N(x)| ≤ M_N+1 |w_N+1(x)| / (N+1)!,

где

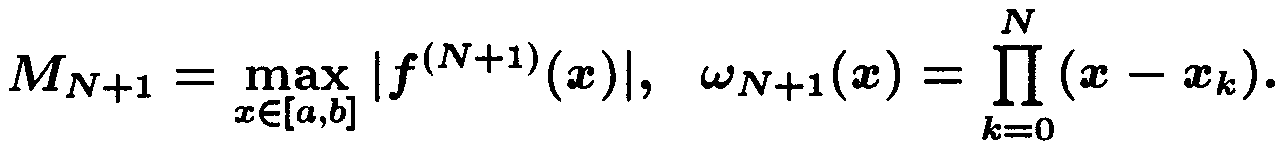
ДОКАЗАТЕЛЬСТВО: Определим вспомогательную функцию

u(x)=f(x) - P_N(x) - K w_N+1(x),

где K - некоторая константа. Очевидно, что u(x) имеет N+1 корень x₀ , x₁ , ..., x_N :

u(x_i )=f(x_i ) - P_N(x_i ) - K w_N+1(x_i )=0, i=0, ..., N.

Подберем константу K так, чтобы функция u(x) имела (N+2)-ой корень в произвольной точке x^*[a,b] причем x^*≠x_i , i=1, ..., N. Имеем

0=u(x^*)=f(x^*) - P_N(x^*) - Kw_N+1(x^*)

откуда следует, что

K = (f(x^*) - P_N(x^*)) / w_N+1(x^*)

Итак, при такой константе K функция u(x) имеет N+2 корня на отрезке [a,b] и, следовательно, обращается в ноль на концах каждого из (N+1)-го элементарного отрезка:

[x₀ , x₁], [x₁ , x₂], ..., [x_i , x^*], [x^* , x_i+1], ..., [x_N-1 , x_N].

По теореме Ролля u'(x) имеет не менее (N+1)-го корня внутри [a,b] (по количеству отрезков).

Аналогично u''(x) имеет не менее N корней внутри [a,b]. Рассуждая таким образом, в результате получим, что u^(N+1)(x) имеет не менее одного корня внутри отрезка [a,b]. Пусть ξ (a,b) - этот корень: u^N+1(ξ)=0. Найдем (N+1)-ую производную функции u(x): u^(N+1)(x)=f^(N+1)(x)-K(N+1)! (так как P_N(x) - полином степени N, а w_N+1(x) - степени N+1).

Тогда

0 = u^N+1(ξ) = f ^N+1(ξ) - K(N+1)!

Следовательно,

K = f ^N+1(ξ ) / (N+1)!

Сравнивая это выражение с предыдущим представлением для K, находим

(f(x^*) - P_N(x^*)) / w_N+1(x^*) = f ^N+1(ξ) / (N+1)!

Отсюда следует

f(x^*) - P_N(x^*) = w_N+1(x^*) f ^N+1(ξ) / (N+1)!

Вспоминая, что точка x^* выбиралась произвольной на [a,b]\{x₀ , x₁ , ..., x_N}, опускаем звездочку при x и получаем требуемую оценку:

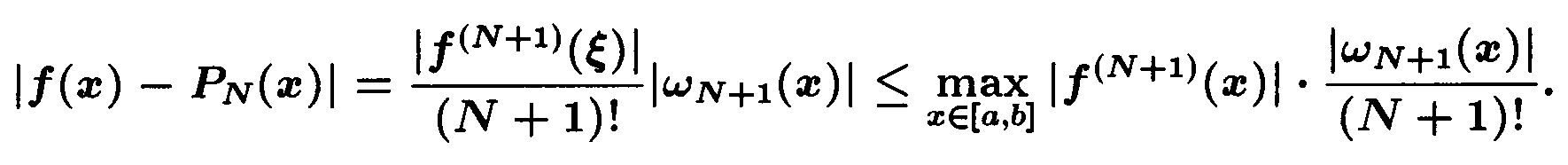
Если же x=x_i для некоторого i, то оценка также верна: