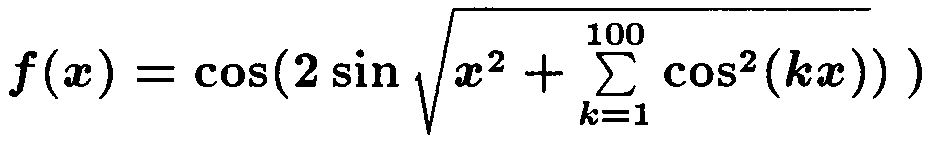Постановка задачи. Кусочно-линейная интерполяция.

При решении ряда задач требуется восстановить функцию y=f(x) для произвольного значения x на отрезке [a,b], если известны ее значения в некотором конечном числе точек этого отрезка (найденных, например, в результате эксперимента). Кроме того, функция y=f(x) может быть задана формулой, вычисление значений которой очень трудоемко (например, 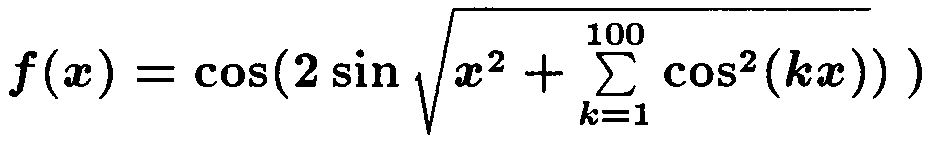и требуется иметь для f(x) более простую формулу, которая позволяла бы находить значения f(x) в любой точке с заданной точностью e. Данная задача решается путем интерполяции.

Математическая постановка.

Пусть известные значения некоторой функции y=f(x) образуют на отрезке [a,b] следующую табличную функцию:

x	x0	x1	...	xN
f	f0	f1	...	fN

Таблица 3.1: Табличная функция.

где a ≡ x₀ < x₁ < ... < x_N ≡ b.

Требуется построить интерполянту - функцию F(x), совпадающую с f(x) в точках x_i:

F(xi ) = fi , i=0, ..., N	(3.1)

Определение 3.1 Нахождение функции-интерполянты F(x) называют интерполяцией, а точки x₀ , x₁ , ... , x_N - узлами интерполяции. Величины h_i=x_i - x_i-1 , i = 1, ..., N - называют шагами табличной функции.

Основная цель интерполяции - получить быстрый алгоритм вычисления значений F(x) для xÎ[a,b], не содержащихся в таблице данных.

Основные вопросы:

1) Выбор интерполянты F(x).

2) Оценка погрешности интерполяции: |f(x) - F(x)|

Простейшим видом интерполяции является кусочно-линейная интерполяция. Она состоит в том, что заданные точки (x_i , f_i ), i = 0, ..., N соединяются прямолинейными отрезками, и функция f(x) приближается полученной ломаной.

Уравнения каждого отрезка ломаной в общем случае разные. Поскольку имеется N интервалов (x_i-1 , x_i), то для каждого их них в качестве уравнения интерполянты используется уравнения прямой, проходящей через две точки. В частности, для i-го интервала можно написать уравнение прямой, проходящей через точки (x_i-1 , f_i-1 ) и (x_i , f_i ), в виде

(y - f_i-1 )/(f_i - f_i-1 ) = (x - x_i-1 )/(x_i - x_i-1 )

Отсюда

y = aix + bi ≡ F(x), x (xi-1, xi) ai = (fi - fi-1 )/(xi - xi-1 ), bi = fi-1 - aixi-1 , i = 1, ..., N	(3.2)

Следовательно, при использовании кусочно-линейной интерполяции сначала нужно определить номер i интервала, в который попадает значение аргумента x, затем подставить x и i в формулу (3.2) и найти приближенное значение функции в точке x.

Если f(x) C ² [a, b], то оценка погрешности при кусочно-линейной интерполяции имеет вид

|f(x) - F(x)| ≤ M₂ h²/2,

где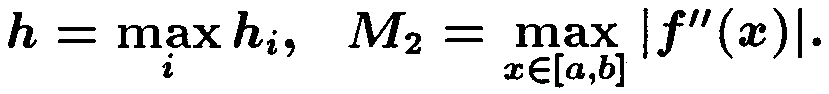

Доказательство этого факта непосредственно следует из теоремы о погрешности при интерполяции полиномами, которая будет доказана далее.

В следующих параграфах рассмотрим два других вида интерполяции: интерполяция полиномами и сплайн-интерполяция.