Модификации метода Ньютона.

Метод секущих для нелинейного уравнения.

В формуле

x^(k+1) = x^(k) - f(x^(k))/f '(x^(k)) , k = 0, 1, 2, ...

метода Ньютона требуется вычислять производную функции f(x), что не всегда удобно, а иногда практически невозможно. В методе секущих производная f '(x^(k)) заменяется на дробь (так называемую разделенную разность) (f(x^(k)) - f(x^(k-1))) / (x^(k) - x^(k-1)).

В результате формула метода принимает вид:

x(k+1) = x(k) - f(x(k))(x(k) - x(k-1)) / (f(x(k)) - f(x(k-1))), k = 1, 2, ...	(2.19)

где x⁽⁰⁾,x⁽¹⁾ - некоторые начальные приближения к корню.

Геометрический смысл метода секущих заключается в замене на итерации с номером k графика функции y=f(х) на секущую, проходящую через точки (x^(k),f(x^(k))) и (x^(k-1),f(x^(k-1))) и, следовательно, задаваемую уравнением

y = (f(x^(k)) - f(x^(k-1)))(x - x^(k))/ (x^(k) - x^(k-1)) + f(x^(k))

Далее находим точку ее пересечения с осью OX, что соответствует решению линейного уравнения:

(f(x^(k)) - f(x^(k-1)))(x - x^(k))/ (x^(k) - x^(k-1)) + f(x^(k)) = 0

Отсюда получаем:

x = x^(k) - f(x^(k))(x^(k) - x^(k-1)) / (f(x^(k)) - f(x^(k-1))) ≡x^(k+1)

1) В общем случае сходимость по методу Ньютона происходит быстрее, чем по методу секущих, и кроме того не требуется нахождения сразу двух начальных приближений к искомому корню. Но при использовании метода секущих не требуется вычисления производной.

2) Условие окончания итераций в методе секущих остается тем же, что и в классическом методе Ньютона: | x^(k+1) - x^(k) | ≤ ε.

Метод хорд для нелинейного уравнения.

В методе хорд производная f '(x^(k)) метода Ньютона заменяется на еще более простую (по сравнению с методом секущих) разделенную разность (f(x^(k)) - f(x⁽⁰⁾)) / (x^(k) - x⁽⁰⁾)

В результате формула метода хорд принимает вид:

x(k+1) = x(k) - f(x(k))(x(k) - x(0)) / (f(x(k)) - f(x(0))), k = 1, 2, ...	(2.20)

причем x⁽⁰⁾, x⁽¹⁾ - некоторые начальные приближения к корню. Геометрически рассматриваемый метод означает замену на каждой итерации графика функции y=f(х) на хорду, то есть через точки (x⁽⁰⁾,f(x⁽⁰⁾)) и (x^(k),f(x^(k))) проводим хорду

y = (f(x^(k)) - f(x⁽⁰⁾))(x - x^(k))/ (x^(k) - x⁽⁰⁾) + f(x^(k))

и находим точку ее пересечения с осью OX, что соответствует решению линейного уравнения:

(f(x^(k)) - f(x⁽⁰⁾))(x - x^(k))/ (x^(k) - x⁽⁰⁾) + f(x^(k)) = 0

Выражая отсюда x, получаем:

x = x^(k) - f(x^(k))(x^(k) - x⁽⁰⁾) / (f(x^(k)) - f(x⁽⁰⁾)) ≡ x^(k+1)

ЗАМЕЧАНИЕ 2.6 Критерий окончания итераций в методе хорд имеет вид:

| x^(k+1) - x^(k) | ≤ ε

Упрощенный метод Ньютона.

Этот метод имеет вид

x(k+1) = x(k) - f(x(k))/f '(x(0)) , k = 0, 1, 2, ...	(2.21)

где x⁽⁰⁾ - некоторое начальное приближение к корню.

Критерий окончания данного итерационного процесса имеет вид:

| x^(k+1) - x^(k) | ≤ ε

К достоинствам этого метода следует отнести простоту его реализации и возможность обобщения на системы уравнений (см. следующий параграф), а к недостаткам - более медленную по сравнению с методом Ньютона сходимость.

Модификация метода Ньютона для системы двух уравнений.

Для решения системы из двух уравнений

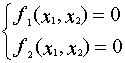
используется следующая модификация метода Ньютона:

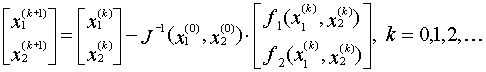	(2.22)

где (x₁⁽⁰⁾, x₂⁽⁰⁾) - некоторое начальное приближение к искомому корню.

ЗАМЕЧАНИЕ 2.7 1) В данном методе в отличие от классического метода Ньютона обратную матрицу требуется подсчитывать только один раз.

2) Условие окончания итерационного процесса имеет вид: || x^(k+1) - x^(k) || ≤ ε