[0, A], где A = max(1,a).
В качестве начального приближения к корню можно взять, например,
x(0) = A/2
Метод Ньютона.
Метод Ньютона для нелинейного уравнения.
Для решения нелинейного уравнения f(x)=0 по методу Ньютона используется итерационный процесс:
| x(k+1) = x(k) - f(x(k))/f '(x(k)) , k = 0, 1, 2, ... | (2.15) |
|---|
где x(0) - некоторое начальное приближение к корню.
При этом предполагается, что f '(x)≠ 0 на отрезке [a,b].
Геометрический вывод формулы.
Геометрически итерационный процесс метода Ньютона означает замену на
k-той итерации графика функции y=f(x) на касательную к этой функции
в точке (x(k) , f(x(k))) (в связи с этим метод также иногда
называется методом касательных).
Уравнение касательной имеет вид
y=f '(x(k))(x-x(k))+f(x(k))
Найдем точку пересечения с осью OX этой касательной
(вместо функции y=f(x)),
что соответствует нахождению решения линейного уравнения:
f '(x(k))(x-x(k))+ f(x(k))=0
вместо нелинейного f(x)=0.
Выражая x, получаем: x = x(k) - f(x(k))/f '(x(k))≡ x(k+1)
Аналитический вывод формулы.
Рассмотрим уравнение f(x)=0, X - его корень, x(k) - k-ое приближение к корню. Тогда по теореме Лагранжа о средних значениях имеем: 0 = f(X) = f(x(k)) + (X - x(k) )f '(ck ), где ck ∈ (X, x(k) ). Заменяя f '(ck) на значение f '(x(k) ) (то есть используя предыдущее приближение к корню) приходим к приближенному равенству 0 ≈ f(x(k)) + (X - x(k))f '(x(k)). Откуда получаем X ≈ x(k) - f(x(k))/f '(x(k)) ≡ x(k+1)
Сходимость метода Ньютона.
Для исследования сходимости метода Ньютона перепишем его в виде частного случая метода простой итерации, достаточные условия сходимости которого уже известны. Имеем:
x(k+1) = x(k) - f(x(k))/f '(x(k))
Следовательно,
x(k+1) = φ(x(k)), где φ(x) = x - f(x) / f '(x)
Проверим следующее условие теоремы о сходимости метода простой итерации:
| |φ '(x)| ≤ q < 1. | (2.16) |
|---|
В случае метода Ньютона имеем:
| φ '(x) = 1 - [(f '(x))2 - f ·f ''] / (f ')2 | (2.17) |
|---|
Пусть корень X уравнения f(x)=0 имеет кратность p ≥ 1. Тогда в достаточно малой окрестности корня X имеет место представление:
f(x) ≈ a(x-X) p
Следовательно
φ '(x) = f ·f ''/(f ') 2 ≈ a(x-X) pa·p(p-1)(x-X) p-2/[a·p(p-1)(x-X) p-1] 2 =
= (p-1)/p < 1
Таким образом в некоторой окрестности корня X условие (2.16) выполнено с константой q < 1.
ЗАМЕЧАНИЕ 2.3
1) Метод Ньютона является наиболее часто используемым для нахождения корней произвольной дифференцируемой функции, особенно если известны достаточно точные начальные приближения для корней.
2) При вычислении корня уравнения с точностью ε по методу Ньютона условием окончания итераций может служить:
| x(k+1) - x(k) | ≤ ε
ПРИМЕР 2.2 Построим итерационный процесс Ньютона для нахождения корня уравнения f(x)≡x2 - a = 0, где a>0 (отметим, что решение данного уравнения равносильно извлечению квадратного корня из произвольного положительного числа a).
Общая формула метода Ньютона принимает в данном случае вид:
x (k+1) = x (k) - ( [x (k)] 2 - a) / (2x (k)) = [x (k) + a / (2x (k))], k = 0, 1, ...
Очевидно, что X [0, A], где A = max(1,a).
В качестве начального приближения к корню можно взять, например,
x(0) = A/2
Метод Ньютона для системы двух уравнений.
Рассмотрим систему двух уравнений
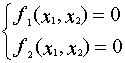
Алгоритм решения системы по методу Ньютона задается формулами:
 |
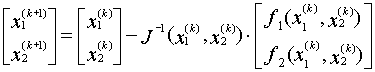(2.18) |
|---|
где
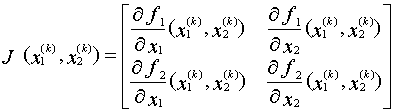
и (x1(0), x2(0)) - некоторое начальное приближение к корню.
ЗАДАЧА 2.1 Вывести координатное представление метода Ньютона.
ЗАМЕЧАНИЕ 2.4 Критерием окончания итерационного процесса Ньютона для вычисления корня системы уравнений с точностью e может служить:
|| x (k+1) - x (k) || ≤ ε.