Методы решения нелинейных уравнений и систем нелинейных уравнений.

Большинство нелинейных уравнений и систем, встречающихся на практике, невозможно решить в явном виде. Приведем в качестве примера следующее уравнение

cos(x) - x = 0

и систему:

x₁ + x₂ = 1
cos(x₁) + x₂ = 0

В подобных случаях применяются численные методы. Более того, многие из тех задач, которые возможно решить аналитическими методами нередко гораздо быстрее и эффективнее решаются численными методами с требуемой точностью.

Будем далее в этой главе обозначать через x число x R¹ в случае решения одного уравнения и вектор x = (x₁ , ..., x_n ) Rⁿ в случае решения системы уравнений.

Постановка задачи. Отделение корней. Метод деления пополам.

Решение уравнения f(x)=0 и системы уравнений F(x)=0 состоит из двух этапов:

1) Отделение корней, то есть отыскание достаточно малых областей, в каждой из которых заключен ровно один корень уравнения или системы уравнений.

2) Вычисление каждого отделенного корня с заданной точностью.

Отделение корней можно произвести графически с сопутствующим анализом на монотонность, смену знака, выпуклость функции. В частности, полезны следующие сведения из математического анализа:

1) Если f : [a,b] → R - непрерывная строго монотонная функция и
f(a)· f(b)<0, то на отрезке [a,b] существует единственный корень уравнения f(x)=0.

2) Признак строго монотонного убывания (возрастания) дифференцируемой функции y=f(x) на отрезке [a,b]: f '(x) < 0 (> 0) на [a,b].

3) Признак строгой выпуклости вверх (вниз) дважды дифференцируемой функции y=f(x) на отрезке [a,b]: f "(x) < 0 (> 0) на [a,b].

Укажем следующие три способа отделения корня для случая x R¹:

1) Составляется таблица значений функции y=f(x) на промежутке изменения аргумента x, и если окажется, что для соседних значений аргументов значения функции имеют разные знаки, то корень уравнения
f(x)=0 находится между ними.

2) Строится график функции f(x)=0 на промежутке изменения аргумента x; тогда искомые корни находятся в некоторых окрестностях точек пересечения графика с осью OX.

3) Уравнение f(x)=0 заменяется равносильным φ(x)=ψ(x). Строятся графики функций y=φ(x) и y=ψ(x); тогда искомые корни находятся в некоторых окрестностях проекций на ось OX точек пересечения этих графиков.

В дальнейшем будем полагать, что корни уже отделены.

Для вычисления отделенного корня существует множество методов. Из них мы рассмотрим следующие: метод деления пополам, метод простой итерации, метод Ньютона и его модификации.

Простейшим методом является метод деления пополам, называемый также методом бисекций или методом дихотомии. Он состоит в следующем. Допустим, что удалось найти отрезок [a,b], на котором расположен один корень X. В качестве начального приближения к корню принимаем середину этого отрезка: x⁽⁰⁾=(a+b)/2. Далее исследуем значение функции f(x) на концах отрезков [a,x⁽⁰⁾] и [x⁽⁰⁾,b], то есть в точках a, x⁽⁰⁾, b. Тот из отрезков, на концах которого f(x) принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового исследуемого отрезка. Вторую половину отрезка [a,b] не рассматриваем (так как корня там нет). В качестве первого приближения к корню принимаем середину нового отрезка и т.д. После каждого приближения (итерации) отрезок, на котором расположен корень, уменьшается вдвое, то есть после k-ой итераций он сокращается в 2^k раз.

Математически формулы метода деления пополам представляются следующим образом: .

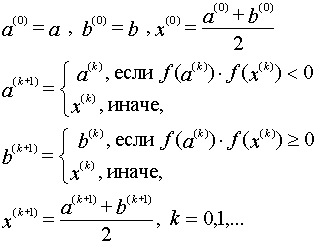Итерационный процесс следует продолжать до тех пор, пока значение функции f после некоторой итерации с номером k+1 не станет по модулю меньше либо равно некоторого заданного малого числа ε, то есть
| f(x ^(k+1)) | ≤ ε. После этого с погрешностью ε полагают: X ≈ x ^(k+1).

ЗАМЕЧАНИЕ 2.1 Другим вариантом условия окончания итераций может служить (b ^(k+1) - a ^(k+1) )/ 2 ≤ ε.

Это условие следует из очевидного неравенства

|X - x ^(k+1)| ≤ (b ^(k+1) - a ^(k+1) )/ 2.