Метод прогонки

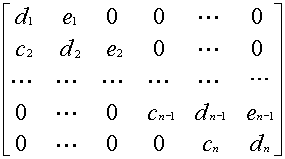
Для решения систем A x = b с трехдиагональной матрицей наиболее часто применяется метод прогонки, являющийся адаптацией метода Гаусса к этому случаю.

Запишем систему уравнений

    d₁x₁ + e₁x₂                                            = b₁
           c₂x₁ + d₂x₂ + e₂x₃                                 = b₂
                      c₃x₂ + d₃x₃ + e₃x₄                      = b₃
                                    ...       ...       ...
                                 c_n-1x_n-2 + d_n-1x_n-1 + e_n-1x_n = b_n-1
                                                    c_nx_n-1 + d_nx_n = b_n

в матричном виде: A x = b где

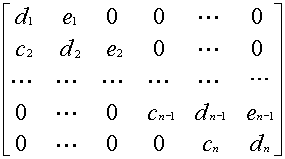
Выпишем формулы метода прогонки в порядке их применения.

Прямой ход метода прогонки (вычисление вспомогательных величин):

a₂ = -e₁ / d₁
b₂ = b₁ / d₁
a_i+1 = -e_i / [d_i + c_ia_i], i=2, ..., n-1
b_i+1 = [-c_ib_i + b_i] / [d_i + c_ia_i], i=2, ..., n-1
(1.9)
Обратный ход метода прогонки (нахождение решения):

x_n = [-c_n b_n + b_n] / [d_n + c_na_n]
x_i = a_i+1 x_i+1 + b_i+1, i = n-1, ..., 1 (1.10)

a₂ = -e₁ / d₁ b₂ = b₁ / d₁ a_i+1 = -e_i / [d_i + c_ia_i], i=2, ..., n-1 b_i+1 = [-c_ib_i + b_i] / [d_i + c_ia_i], i=2, ..., n-1	(1.9)

x_n = [-c_n b_n + b_n] / [d_n + c_na_n] x_i = a_i+1 x_i+1 + b_i+1, i = n-1, ..., 1	(1.10)

Метод прогонки можно применять, если нигде в формулах знаменатели не равны нулю. В [2, стр.134] доказано следующее

УТВЕРЖДЕНИЕ 1.1 Для применимости формул метода прогонки достаточно выполнения условий диагонального преобладания у матрицы A, то есть

| d_i | ≥ | c _i | + | e_i |

причем хотя бы одно неравенство должно быть строгим.