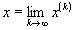Классификация методов. Сведения о матрицах.

Многие задачи математического анализа, дифференциальных и интегральных уравнений сводятся при численном решении к решению задач линейной алгебры и, в частности, к решению системы линейных алгебраических уравнений (кратко - СЛАУ) вида:

	a11 x1 + a12 x2 + ... + a1n xn = b1       a21 x1 + a22 x2 + ... + a2n xn = b2 ...       an1 x1 + an2 x2 + ... + ann xn = bn	(1.1)

которая в матричной форме примет вид:

Ax=b	(1.2)

где

x = (x1 , ..., xn )T, b = (b1 , ..., bn )T, A = (aij )	(1.3)

Везде далее предполагается, что det(A) ≠ 0

Методы решения большинства задач численных методов (в том числе задач решения линейных алгебраических систем) можно разделить на два типа: прямые и итерационные.

Определение 1.1 Метод решения задачи называется прямым, если он дает ее точное решение за конечное число действий.

Заметим, что при реализации прямого метода на ЭВМ вообще говоря возникает вычислительная погрешность, связанная с конечным числом разрядов ЭВМ для представления вещественных чисел.

Определение 1.2 Метод решения задачи называется итерационным, если он дает точное решение как предел последовательности приближений, вычисляемых по единообразной схеме, то есть 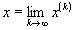где x - точное решение задачи, x^(k) - k-тое приближение (итерация) к решению.

При реализации итерационного метода на ЭВМ его приходится обрывать на каком-то приближении с номером K и полагать x ≈ x^(k) . Обычно указывают погрешность (точность) ε, с которой требуется найти решение x и условие окончания итераций задают таким образом, чтобы норма разности точного решения и очередного итерационного приближения не превышала ||x - x^(k)|| ≤ ε. Типичные значения задаваемой погрешности ε находятся в диапазоне 10^-3 - 10^-8.

К прямым методам решения СЛАУ относятся известный из алгебры метод Крамера, метод Гаусса и его модификации и другие, к итерационным - метод простой итерации, метод Зейделя и другие.

Напомним основные понятия и определения норм в пространстве векторов и матриц.

Пусть в пространстве векторов {x Rⁿ: x = (x₁ , ..., x_n )^T} введена норма ||x||. Тогда норма ||A|| в пространстве матриц {A Rⁿ×Rⁿ: A = (a_ij)} называется согласованной с нормой вектора, если для любой матрицы A и для любого вектора x выполняется неравенство

||Ax|| ≤ ||A|| · ||x||	(1.4)

В качестве примера приведем следующие согласованные нормы:

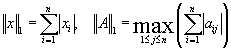
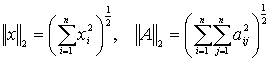
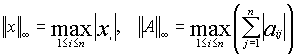
В дальнейшем будут всегда использоваться только согласованные векторные и матричные нормы.

Определение 1.3

1. Матрица A называется симметричной, если A^T = A.
2. Матрица A называется трехдиагональной, если все элементы, не находящиеся на главной диагонали и ее соседних (наддиагонали и поддиагонали), равны нулю.
3. Верхней(нижней) треугольной называется такая матрица, у которой равны нулю все элементы, расположенные ниже(выше) главной диагонали.
4. Говорят, что матрица A - с диагональным преобладанием, если
   |a_ii| ≥ ∑ ⁿ_{j = 1, j} ≠ i|a_ij|, i = 1, ..., n, причем хотя бы одно неравенство является строгим. Если все неравенства строгие, то говорят, что матрица A - со строгим диагональным преобладанием.