ЭЛЕМЕНТЫ КВАНТОВОЙ ОПТИКИ

Лабораторная работа N⁰17

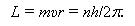
Градуировка спектроскопа. Изучение спектра водорода.

Цель работы: градуировка спектроскопа по известным длинам волн линейчатого спектра водорода. Исследование серии Бальмера в видимой области спектра.

Оборудование: спектроскоп, генератор, спектральные трубки, ВС-24М, соединительные провода.

Введение

Как известно, раскаленные твердые и жидкие тела, а также газы большой плотности, независимо от их состава испускают полосатые и линейчатые спектры. Полосатые спектры испускаются возбужденными молекулами газа, линейчатые - атомами. Обычно полосатые спектры испускаются не очень разреженными, а линейчатые - очень разреженными газами (или парами). Все металлы в газообразном состоянии также дают линейчатые спектры. Каждый химический элемент испускает типичный для него спектр. Для анализа спектров служат спектральные приборы. Одним из простейших спектральных приборов является спектроскоп (рис.23).

Спектроскопом называется прибор, служащий для пространственного разделения лучей различных длин волн, причем наблюдение полученного спектра в целом или отдельных спектральных линий производится визуально. Оптическая схема простейшего спектроскопа дана на рис. 24.

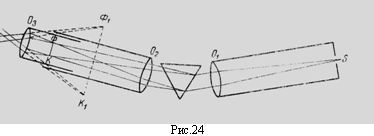
Основной частью спектроскопа является призма (1 на рис. 23), которая разлагает в спектр пучок параллельных лучей немонохроматического света. Правая часть прибора - коллиматорная труба (3 на рис.23) - состоит из узкой щели S и линзы O₁; щель располагается в главной фокальной плоскости линзы O₁. Пучок, исходящий из щели, после прохождения через линзу становится параллельным и падает на призму. Так как лучи разной длины волны отклоняются призмой на разные углы (дисперсия), то из призмы выходят параллельные пучки различных направлений. С помощью второй линзы O₂ параллельные пучки собираются в различных точках ее фокальной плоскости. В результате в фокальную плоскость проектируется ряд изображений входной щели. Если источник света излучает волны всевозможных длин (например, лампочка накаливания), то все изображения входной щели в различных лучах непосредственно примыкают друг к другу, т.е. получается сплошной спектр. При излучении же источником света волн лишь определенных длин волн (газоразрядные трубки), изображения входной щели окажутся пространственно разделенными, и в результате получится линейчатый спектр.

В фокальной плоскости линзы О₂ в спектроскопе устанавливается окуляр О₃ (6 на рис.23) для визуального наблюдения. Если поворачивать призму, то в центре окуляра будут по очереди размещаться лучи с различными длинами волн. Поскольку в спектроскопах поворот призмы осуществляется при помощи барабана (7 на рис. 23) с делениями, то каждому положению барабана соответствует определенная длина волны входящего света. Градуировочный график спектроскопа выражает зависимость между длиной волны входящего светового пучка и делениями барабана.

Теория водородоподобных атомов Бора

Основываясь на гипотезе Планка о квантовом характере излучения и поглощения света, Бор сформулировал законы движения электрона в атоме в виде постулатов, которые дали объяснения экспериментальным фактам.

1 постулат. Электрон в атоме может вращаться только по строго определенным орбитам, радиус которых r определяется из условия:

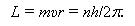(17.1)

Здесь L- момент количества движения электрона, m - его масса, ν - скорость электрона, h- постоянная Планка, n = 1, 2, 3,... - квантовые числа, определяющие принадлежность электрона к той или иной орбите. Все прочие орбиты являются "запрещенными". Таким образом, Бор постулировал, что энергия электрона в атоме может принимать лишь строго определенные значения.

2 постулат. Вращаясь по стационарным орбитам, электрон не излучает. Излучение происходит лишь при переходе электрона из стационарного состояния с большим значением энергии E_m в другое стационарное состояние с меньшим значением энергии E_n.

При этом излучается квант света, частота которого определяется из условия:

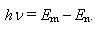(17.2)

Из формулы (17.2) следует, что излучение происходит при переходе электрона с внешних орбит на внутренние. Если возбужденный электрон переходит с внутренних орбит на внешние, то происходит поглощение энергии.

Радиус стационарных орбит r и полная энергия электрона E в водородоподобном атоме с зарядом ядра ze определяется соотношениями:

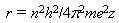	(17.3)
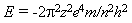	(17.4)

Из формулы (17.4) следует, что квантовое число n определяет энергию электрона в атоме, т.к. остальные величины остаются постоянными. В общем случае атомная система, состоящая из ядра и одного электрона, переходит из стационарного состояния, характеризуемого квантовым числом m в состояние с квантовым числом n(n< m) испускает по третьему постулату Бора линия спектра с частотами:

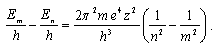(17.5)

Величина

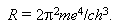(17.6)

называется постоянной Ридберга. Произведя замену в выражении (17.5), получим:

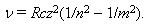(17.7)

Вычисленное по формуле (17.6) значение постоянной Ридберга с большой точностью совпадает с экспериментальным. В разреженных газах или в парах металлов взаимодействие между отдельными атомами незначительно. Поэтому спектры таких газов состоят из отдельных спектральных линий различных частот, также подчиняющихся уравнению (17.7).

Т.к. ν= с/λ, то формулу (17.7) можно записать в виде:

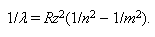(17.8)

Формула (17.8) является одной из наиболее точных формул физики.

Все линии спектра водорода могут быть объединены в серии. Серией называют совокупность линий, описываемых формулой (17.8) при n = const, т.е. серия возникает при переходе электрона с вышележащих орбит m на орбиту с данным квантовым числом n, m = n + 1, n + 2, ... Для водорода (z = 1) основными сериями являются: n = 1 - серия Лаймана, n = 2 - серия Бальмера, n = 3 - серия Пашена, n = 4 - серия Пфунда (рис. 25).

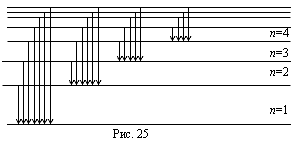
Некоторые серии спектра водорода, в частности Бальмера, были получены экспериментально до создания теории Бора. Видимая часть линейчатого спектра водорода (серия Бальмера) состоит из ряда линий, наиболее яркими из которых являются следующие четыре: красная Н_α (m = 3); голубая Н_β (m = 4); фиолетовая H_γ (m= 5); фиолетовая H_δ (m = 6).

Выполнение работы

Упр. 1. Градуировка спектроскопа.

Градуировка спектроскопа заключается в построении градуировочного графика спектроскопа по известным длинам волн линейчатого спектра известного газа, для чего по оси Х откладывают показания барабана, а по оси У длины волн. Для этого пользуются спектральными трубками, наполненными специально очищенными газами, находящимися под давлением около 1 мм рт. ст. и имеющими в средней части капилляр, где при пропускании разряда происходит наиболее интенсивное свечение. Не следует заставлять ее работать в то время, когда не производится наблюдение, так как от продолжительной работы трубка начинает светиться менее интенсивно.

Щель предварительно установленного спектроскопа следует как можно ближе придвинуть к капилляру спектральной трубки, причем она должна быть расположена параллельно капилляру, т.е. вертикально. При использовании водородной трубкой необходимо направлять спектроскоп на наиболее яркий интенсивно окрашенный участок.

Градуировка барабана спектроскопа можно вести по любой трубке, если известны длины волн находящегося в ней газа. Длины волн для градуирования, их расположение и цвет даны в таблице.

Таблица

Длины волн некоторых спектральных линий в нм

Измерение и обработка результатов

1. Устанавливают трубку с гелием, азотом или неоном и включают ток.
2. Наблюдая спектр гелия, азота или неона и осторожно вращая барабан приводят указатель окуляра оптической трубы спектроскопа с совпадение с первой хорошо различимой линией, например ярко-красной, и делают отсчет по шкале винта и барабана и т.д. Результаты измерений заносят в таблицу, предварительно записав в нее известные длины волн спектра, по которому ведется градуировка.
3. Строят график градуировки λ= λ(n) откладывают по оси Х показания шкалы винта и барабана, а по оси Y- длины волн в данном спектре.
4. Зарисовывают спектр, соблюдая интервалы по длинам волн между спектральными линиями. Показания шкалы винта и барабана спектроскопа вносят в таблицу.

Упр. 2. Определение длины волн линий в спектре водорода.

Источником света является стеклянная трубка с капилляром по середине, наполненная очищенным водородом при давлении около 1 мм рт. ст. Капиллярная часть трубки укрепляется близко к щели так как при включении высокого напряжения в капилляре происходит наибольшее свечение.

Водород - газ, большинство атомов которого объединены попарно в двухатомные молекулы. Так как сериальные закономерности касаются спектра одноатомного водорода, то наблюдение этого спектра в обычных условиях затруднено тем, что на линейчатый спектр атомного водорода накладывается полосатый спектр молекулярного водорода, т.е. происходит одновременное излучение обоих спектров. Но так как характер их различен, то можно наблюдать интересующие нас линии серии Бальмера. Первая головная линия серии Бальмера Н_α - ярко-красная линия, вторая Н_β - зелено-голубая. В промежутке между этими линиями имеется ряд слабых красно-желтых и темно-зеленых молекулярных полос: их во внимание не брать. Третья линия Н_γ - синяя, ей предшествуют две слабые размазанные фиолетовые молекулярные полосы. Четвертая линия Н_δ - слабо-фиолетовая (в нашей установке видна плохо).

Таблица 2

Определение длин волн спектральных линий водорода

Измерения и обработка результатов

1. Устанавливают осветитель перед щелью спектроскопа и включают его. Определяют длину волны красной линии, для чего совмещают указатель окуляра с красной линией спектра и производят отсчет по шкале винта и барабана. Затем, используя градуировочную кривую из первого упражнения, определить длину волны.
2. Аналогично вычислить длины волн трех других линий.
3. Подсчитать волновые числа N = 1/λ для всех линий.
4. Все результаты свести в таблицу. Рассчитать постоянную Ридберга по формуле R=(1/λ)/(1/n² - 1/m²) для всех длин волн, затем рассчитать ее среднее значение R_ср по формуле (0.3) и погрешность ΔR по формуле (0.4). Результат представить в виде R=R_ср±ΔR.

Контрольные вопросы

1. Законы преломления. Преломления света в призме.
2. Дисперсия света.
3. Устройство и принцип работы спектроскопа.
4. Линейчатые спектры. Излучение атомов. Постулаты Бора.
5. В чем заключается спектральный анализ?