Определение коэффициента преломления стеклянной пластинки с помощью микроскопа
Оборудование: микроскоп с микрометром, стеклянная пластинка.
Теория
Предмет, рассматриваемый через плоскопараллельный слой прозрачного вещества, имеющего большую оптическую плотность, по сравнению с воздухом, кажется нам расположенным ближе. Представим себе, что мы рассматриваем точку О через плоскопараллельную стеклянную пластинку (рис.16). Проведем из точки О два луча ОВ и ОС. После преломления эти лучи пройдут по направлениям СД и ВЕ. Наблюдая сверху, мы увидим, точку О на пересечении продолжения лучей ДС и ВЕ, т.е. в точке О'. Таким образом, точка О покажется нам расположенной ближе на величину а = ОО'. Найдем связь между показателем преломления стекла n, толщиной пластинки d и величиной кажущегося поднятия точки а. Из рис. 16 следует, что
d/b= ctg r;
b/(d-a)=tg i
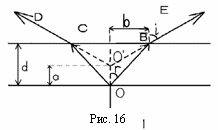
Перемножая полученные выражения, имеем:
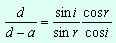
Принимая во внимание (II.1), после преобразований получим
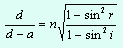
При i→0, r→0, d/(d-a)→n. Таким образом, при наблюдении вертикально сверху
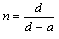 |
(14.1) |
Описанным выше явлением кажущегося поднятия предмета пользуются при определении показателя преломления стеклянной пластинки при помощи микроскопа.
Измерения
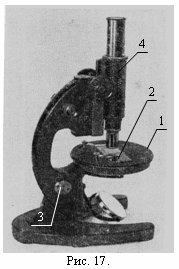
Исследуемую пластинку кладут на предметный столик микроскопа 1 (см. рис.17). Фокусируют микроскоп на верхнюю поверхность пластинки 2, а затем на нижнюю, вращая микрометрический винт 3. На поверхностях пластинки сделаны взаимно перпендикулярные царапины: продольные на верхней и поперечные - на нижней. Очевидно, разность отсчетов микрометрического винта, с помощью которого передвигается тубус микроскопа 4, равна (d-a). Измеряют толщину пластинки d штангенциркулем, и вычисляют показатель преломления стекла n по формуле (14.1). Измерения и расчеты проводятся несколько раз, рассчитывается среднее значение показателя преломления по формуле (0.3) и погрешность опыта по формуле (0.4).
Контрольные вопросы