Лабораторная работа N⁰8

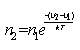
Определение размеров микроскопических (броуновских) частиц методом наблюдения их распределения в поле тяжести

Принадлежности: предметное стекло с приклеенной к нему ванночкой, эмульсия краски (акварельной) в воде, секундомер.

Задание: определить объем частицы краски эмульсии.

Описание приборов

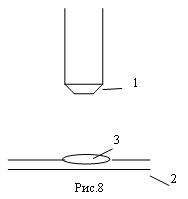
Для определения объемов частиц эмульсии краски используется (рис.8):
1.Микроскоп с микроскопическим винтом (1), позволяющим наблюдать слои на различных уровнях и определять число частиц в этих слоях.
2.Предметное стекло (2) с углублением, куда наливается эмульсия (3).

Краткая теория

При отсутствии внешнего поля газ (совокупность беспорядочно движущихся частиц, молекул) равномерно распределяется по всему предоставленному ему объему: при постоянной температуре концентрация частиц одинакова по всему объему во все частях сосуда.

В случае, если газ будет находиться во внешнем потенциальном поле, например, в поле силы тяжести, распределение молекул газа по высоте уже не будет равномерным.

Больцман показал, что если в том месте, где потенциальная энергия частицы равна U₁, концентрация частиц равна n₁, то в том месте, где потенциальная энергия будет равна U₂, концентрация будет другой, равной

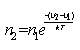(8.1)

где k = 1.38∙10-23 Дж/К - постоянная Больцмана. Эта формула характеризует так называемое распределение Больцмана. Оно справедливо не только для газовых молекул, но и для малых частиц, совершающих беспорядочное тепловое движение.

Для частиц, совершающих броуновское движение, и для молекул газа или жидкости средние кинетические энергии равны друг другу, а разность потенциальных энергий частицы на 2-х уровнях равна работе силы тяжести А₁₂ по перемещению этой частицы с одного уровня на другой:U₁- U₂=A₁₂. По определению работа силы равна произведению силы F на перемещение h=h₁√h₂: A₁₂=Fh. Сила, действующая на частицу в жидкости, складывается из двух сил, направленных в противоположные стороны: силы тяжести P и силы Архимеда F_A
F=P-F_A=mg-ρ₀Vg,
где m - масса частицы, V - ее объем, ρ₀ - плотность жидкости, g - ускорение свободного падения. Так как масса частицы может быть выражена через ее плотность m=ρV, разность потенциальных энергий частицы на разных уровнях может быть представлена в виде

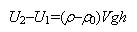(8.2)

Прологарифмировав (8.1), с учетом (8.2) получим
ln(n₁/n₂)=(ρ-ρ₀)gVh/kT
Отсюда

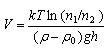(8.3)

Соотношение (8.3) дает возможность определить объем частицы краски. В настоящей работе отношение концентрации частиц на разных высотах можно принять равным отношению средних чисел частиц в поле зрения микроскопа, наблюдаемых в данном слое. Для его определения необходимо подсчитать число частиц, одновременно видимых в окуляр микроскопа сначала на одном уровне, а затем на другом.

Измерения и вычисления

1. Залить ванночку эмульсией частиц краски в воде и поместить на столике микроскопа.
2. Установить микроскоп так, чтобы отчетливо были видны частицы на самом нижнем из возможных уровней.
3. Отсчитать число частиц N, одновременно появляющихся в поле зрения микроскопа в течение каждых 10 секунд, записать данные в таблицу.
4. Произвести 10 таких подсчетов, вычислить среднее число частиц (N_ср) и его погрешность ΔN по формуле (0.4). Надежность принять за 90%. Рекомендуется расчеты вести в статистическом режиме на инженерном калькуляторе (см. с.8). Занести данные в таблицу.
5. Пользуясь микрометрическим винтом (см. рис.17), поднять тубус на 200 микрон и произвести снова 10 таких отсчетов. Определить среднее значение для N.
   

   Таблица

   Результаты измерений зависимости числа броуновских частиц от высоты

   N0	Количество отсчетов за 10 сек
   	h'=0	h'=200 мкм	h'=400 мкм	h'=600 мкм
   1
   2
   ...
   10
   Среднее число частиц Nср
   Погрешность ΔN
   h, мкм

   
   

6. Найти расстояние h между слоями, в которых производились наблюдения. При этом необходимо учесть, что перемещение, отсчитываемое по микрометрическому винту h', дает так называемое оптическое расстояние между уровнями, оно связано с истинным расстоянием соотношением h=nh', где n = 1.33 -показатель преломления воды.
7. Повторить измерения еще для двух высот на 400 мкм и 600 мкм.
8. Постройте график зависимости количества частиц от высоты N_ср(h).
9. Определить объем частиц краски по формуле (8.3). Для этого выберите две точки, максимально близкие к кривой графика зависимости N_ср(h). Температура жидкости принимается равной комнатной. Плотность частиц краски ρ=1.06∙10³ кг/м³, плотность воды ρ₀=1∙10³ кг/м³.

   Контрольные вопросы

   1. Броуновское движение.
   2. Формула Больцмана.
   3. Почему меняется количество частиц с высотой?
   4. Почему в горах воздух разряжен?
   5. Определите высоту, на которую может подняться молекула азота и частица краски с объемом V=10^-21 м³ при Т=280К в поле силы тяжести Земли.
   6. Как изменится концентрация частиц на некоторой высоте при увеличении температуры?