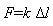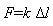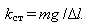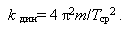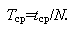Лабораторная работа N06
Определение величины коэффициента жесткости пружины статическим и динамическим методами
Цель:вычислить и сравнить величины коэффициентов жесткости пружины, определенных статическим и динамическим методами.
Приборы и оборудование: штатив, набор пружин различной жесткости, набор грузов, линейка, секундомер.
Обоснование метода
1. Статический метод определения коэффициента упругости
Из закона Гука, определяющего линейную зависимость между механической деформацией тела и деформирующей силой в случае
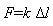 |
(6.1) |
можно определить коэффициент жесткости пружины. Определив удлинение Δl пружины для известной деформирующей силы F, в качестве которой выступает вес Р груза массой m, равный P=mg, определим коэффициент жесткости пружины:
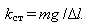 |
(6.2) |
2. Динамический метод определения коэффициента упругости
Из формулы Томсона для пружинного маятника (I.4) выразим коэффициент упругости k:
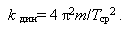 |
(6.3) |
Используя данную формулу, можно рассчитать среднее значение kдин, зная массу тела m, подвешенного на пружине жесткостью k и совершающего колебания малой амплитуды относительно оси пружины, и период Tср, который можно рассчитать, определив, например, время tср для N=30 полных колебаний:
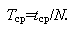 |
(6.4) |
Порядок выполнения работы
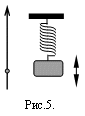
- Соберите пружинный маятник. Для этого на штативе укрепите указанную лаборантом или преподавателем одну из пружин набора, измерив ее начальную длину в недеформированном состоянии l0, и подвесьте к ней один груз известной массы m1 из набора грузов (см. рис.5).
- Измерьте длину пружины в растянутом (деформированном) состоянии l и определите деформацию пружины Δl=l- l0.
- Повторите измерения и расчеты еще для двух грузов массами m2 и m3. Вычислите по формуле (6.2) значения kст и рассчитайте его среднее значение kст ср по формуле (0.3) и погрешность по формуле (0.4).
- Заполните таблицу 1.
Таблица 1
Результаты опыта по определению коэффициента жесткости пружины статическим методом
| Номер опыта |
Масса груза m, кг |
Вес груза P, Н |
Длина пружины |
Деформация Δl, м |
kст, Н/м |
kст ср ±Δkст, Н/м |
| начальная l0, м |
после растяжения l, м |
| 1 |
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
- Не меняя пружины, подвесьте груз массой m1 и измерьте время t1 для N=60 полных колебаний груза малой амплитуды.
- Не меняя пружины и груза, повторите измерения еще 4 раза.
- Найдите среднее время для 60 колебаний tср=(t1+t2+┘+t5)/5 и по формуле (6.4) рассчитайте среднее значение периода колебаний Tср.
- По формуле (0.4) рассчитайте абсолютную Δt и по формуле (0.6) - относительную погрешность времени εt.
- Используя формулу (6.3), рассчитайте среднее значение динамического коэффициента жесткости исследуемой пружины kдин.
- Рассчитайте относительную погрешность коэффициента упругости по формуле εk=2εt, следующей из (0.8), и по формуле (0.9) определите абсолютную погрешность Δk.
- Заполните таблицу 2.
Таблица 2
Результаты опыта по определению коэффициента жесткости пружины динамическим методом
| Номер опыта |
Масса груза m, кг |
Число колебаний N |
Время колебаний t,с |
tср,с |
Период Tср, с |
Коэффициент упругости kдин ср, Н/м |
| 1 |
|
|
|
|
|
|
| 2 |
|
| ... |
|
| 5 |
|
| |
Δt= ; εt= |
εk= ; Δk= ; |
- Сравнив значения kст ср и kдин ср, сформулируйте и запишите вывод.
Контрольные вопросы
- Виды деформации. Закон Гука.
- Что называется жесткостью пружины и от чего она зависит?
- Опишите превращение энергии при колебаниях пружинного маятника.
- Какие силы действуют на груз в опыте? Запишите закон Ньютона для него. Выведите формулу (6.2).