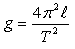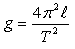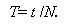Лабораторная работа N⁰5

Определение величины ускорения свободного падения с помощью математического маятника

Цель: вычислить величину ускорения свободного падения и рассчитать абсолютную и относительную погрешности лабораторного эксперимента.

Приборы и оборудование: математический маятник, линейка, секундомер.

Обоснование метода

Из формулы Томсона (I.3) для математического (точечного) маятника выразим g

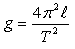(5.1)

Используя данную формулу, можно рассчитать значение g, зная длину маятника l (длину нити + радиус шара, принятого в качестве материальной точки математического маятника!) и период T , который можно рассчитать, определив, например, время t для N=30 полных колебаний:

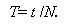(5.2)

Порядок выполнения работы

1. Установите на краю лабораторного стола математический маятник таким образом, чтобы шарик, моделирующий материальную точку, находился не более чем в 5 сантиметрах от пола лаборатории (смотри рис.4).
2. Измерьте с помощью мерной линейки длину маятника l (обязательно посмотрите обоснование метода!).
3. Отклонив маятник от положения равновесия (не более чем на 10 см для получения колебаний малой амплитуды), измерьте время t для N=30 полных колебаний.
4. По формуле (5.2) рассчитайте время одного колебания, т.е. период колебания T.
5. Не меняя условия лабораторного эксперимента, повторите измерения и вычисления T не менее n=3 раза. Полученные данные внесите в таблицу.
6. Вычислите среднее значение периода колебаний T_cp по формуле (0.3). Вместо x подставить в формулу T.
7. Определите абсолютную погрешность измерения периода ΔT по формуле (0.4). Задать уровень надежности 90%.
8. Рассчитайте относительную погрешность ε_T лабораторного эксперимента в процентах по формуле (0.6).
9. По формуле (5.1) рассчитайте среднее значение ускорения свободного падения
10. По формуле (0.8) рассчитайте относительную погрешность измерения ускорения свободного падения
    

    ε_g= 2ε_T

11. Рассчитайте абсолютную погрешность измерения ускорения свободного падения Δg по формуле (0.9)

    Таблица

    Результаты эксперимента по определению ускорения свободного падения с помощью маятника

    N0 опыта	Длина l, м	Число колебаний N	Время t, с	Период T, с	(Ti-Tcp)2	Ускорение свободного падения gср ,м/с2
    1
    2
    ...
    n
    εT= ; εg=				Tcp=,c	ΔT=	Δg=

    
    
12. Запишите результат эксперимента в виде
    g=g_cp±Δg
    и сравните его с истинным значением g=9.8 м/с². Попадает ли оно в интервал значений от g_ср-Δg до g_ср+Δg?

Контрольные вопросы

1. Что называется колебанием? Классификация колебаний.
2. Связь параметров колебаний с параметрами колебательной системы. Формулы Томсона. Зависит ли период колебания от амплитуды?
3. Влияет ли число отсчитываемых колебаний на точность определения времени одного колебания маятника?
4. Опишите превращение энергии при колебаниях.
5. Параметры колебаний: амплитуда, фаза, частота, период.
6. Как изменится период колебаний математического маятника на Луне? Как изменится период колебаний, если увеличить длину нити в 4 раза?