ЧАСТЬ 1.ОСНОВЫ ТЕОРИИ ПОГРЕШНОСТЕЙ

В любых экспериментальных исследованиях проводятся измерения. Эти измерения, как правило, характеризуются определенной точностью. Методы определения точности измерения (его погрешности) разработаны в теории погрешностей.

Погрешности делятся на три класса: приборные, статистические и промахи. Последние представляют собой грубые ошибки при измерениях (описки, результат неправильной работы прибора из-за неисправности или скачка напряжения и т.п.) и какой-то специальной теории для них создать невозможно - существуют лишь методы выделения промахов и их отбраковки, разработанные на свойствах статистических и приборных погрешностей (о них будет сказано ниже).

Приборная погрешность - это точность, с которой прибор может произвести измерение. Например, при помощи линейки размер предмета можно измерить с погрешностью около 1 мм, при помощи микрометра - 10 мкм, а при помощи оптического интерферометра - 0,3 мкм. Естественно, что более точные приборы, как правило, дороже стоят и требуют более высокого уровня знаний и навыков при обращении с ними. Для определения приборной погрешности в первую очередь необходимо ответить на вопрос, имеется ли у прибора класс точности, или нет. У "внеклассных" приборов приборная погрешность Δχ_приб определяется как половина цены деления X_min

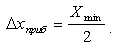(0.1)

Например, у линейки погрешность 0.5 мм.

Класс точности может принимать следующие значения: K=0.1; 0.2; 0.5; 1.0; 2.0; 2.5; 4.0, у электрических приборов он, как правило, написан на панели в правом нижнем углу и определяет точность измерений в процентах. Если класс точности прибора известен ("классный" прибор), то погрешность определяется по формуле

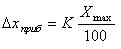(0.2)

X_max - предел шкалы измерений прибора. Например, у вольтметра с классом точности K=1.0 и пределом шкалы измерений U_max=10В, приборная погрешность ΔU_приб=1.0Ч10В/100=0.1В.

Статистическая погрешность вызвана тем, что при достаточной точности прибора при повторном проведении измерения невозможно получить тот же самый результат из-за действия случайных факторов, влияющих на саму измеряемую величину. Например, даже длина предмета при измерениях с точностью до 0.01 мкм будет меняться из-за температурных колебаний и вибрации (предмет то увеличивает свои размеры, то сжимается под их действием). В результате при повторном проведении измерений величины x будет получен целый набор различных значений χ_i , i=1,2,...,n - номер измерения (n - количество измерений). Естественно, что возникает вопрос, какое из них истинное? В качестве оценки такого истинного значения принято среднее значение

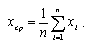(0.3)

Однако, ясно, что с увеличением количества измерений среднее значение может меняться, пока не придет к некоторому пределу, значение которого можно принять за истинное. На практике у нас нет возможности (и необходимости) в проведении столь большого количества измерений, поэтому обычно определяется статистическая погрешность измерения

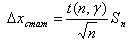	(0.4)
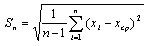	(0.4a)

где t(n,γ) - коэффициент Стьюдента, зависящий от количества измерений n и надежности γ, S_n - срендеквадратичное отклонение. Смысл статистической погрешности состоит в том, истинное значение находится в интервале от χ_cp-Δχ_стат до χ_cp+Δχ_стат с вероятностью γ:

χ_cp-Δχ_стат≤χ_ист≤ χ_cp+Δχ_стат

Коэффициент Стьюдента для различных значений уровня надежности и количества измерений можно определить из следующей таблицы.

Таблица

Значения коэффициента Стьюдента при различных уровне надежности и количестве измерений

Например, при уровне надежности 90% и n=5 получаем t=2.13

Суммарная погрешность, определяемая как приборной, так и статистической погрешностью, рассчитывается по формуле

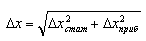(0.5)

Результат расчета погрешности, как правило, округляют до первой значащей цифры, а среднее значение - до порядка погрешности. Например, если в результате расчетов было получено значение среднего χ_cp=12.345678 м, а погрешность составила Δχ=0.123456 м (γ=90%), то результат записывается в виде

χ=12.3±0.1 м при надежности γ=90%.

Ясно, что записывать десятичные цифры меньшего порядка, чем погрешность просто не имеет смысла - при заданной точности измерений мы не можем ручаться, что они имеют именно такое значение.

С тем, что погрешность рассчитывается с точностью до первой значащей цифры, связано важное правило: если приборная погрешность меньше статистической более, чем в два раза (или наоборот, статистическая меньше приборной в два раза), то ей можно пренебречь.

Рассмотренная выше погрешность является абсолютной. Полезной характеристикой измерения является также относительная погрешность, определяемая по формуле

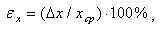(0.6)

которая показывает, какую долю от среднего значения (в процентах) составляет абсолютная погрешность.

До сих пор мы говорили о прямых измерениях. Но довольно часто физическую величину нельзя измерить напрямую, и приходится прибегать к косвенным измерениям. Например, для определения ускорения тела измеряется пройденный им путь S и время движения t, а ускорение определяется по формуле a=2S/t².

Погрешность для величины ƒ, зависящей от напрямую измеряемых величин x, y, z: ƒ=ƒ(x,y,z), для которых известны средние значения x_cp,y_cp,z_cp и погрешности Δx,Δy,Δz , определяется по формуле

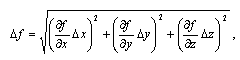(0.7)

где ∂ƒ/∂x,∂ƒ/∂y,∂ƒ/∂z - частные производные величины ƒ от переменных x, y, z (частная производная - это производная функции многих переменных, берущаяся только по одной из них в предположении, что остальные переменные являются константами). Как видим, расчет погрешности по формуле (0.7) не отличается простотой. Однако для большинства практически важных случаев его можно избежать, применяя следующую теорему.

Если величина ƒ является алгебраической функцией от величин x, y, z, то есть при ее расчете используются только арифметические действия и возведение в степень: ƒ=ƒ(x^α,y^β,z^γ) , где α,β,γ - показатели степеней, то относительная погрешность ε_ƒ может быть рассчитана по формуле

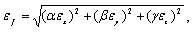(0.8)

где ε_x,ε_y,ε_z - относительные погрешности величин x, y, z. После этого абсолютная погрешность может быть рассчитана по формуле

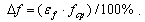(0.9)

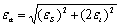В рассмотренном выше примере относительная погрешность ускорения определяется выражением ,а абсолютная вычисляется по формуле (0.9).

Наконец, приведем правило отбраковки выбросов из выборки (правило трех сигм): если одиночное измерение в выборке объемом менее 1000 измерений отклоняется от среднего значения усеченной выборки x_cp , из которой исключено данное измерение, более, чем на три стандартных отклонения S_n-1 , рассчитанных по усеченной выборке,

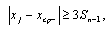(0.10)

оно считается выбросом и отбраковывается.

Здесь

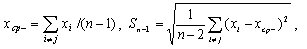(0.11)

Расчет погрешностей на инженерных калькуляторах

В современных инженерных калькуляторах существует статистический режим, в котором удобно производить расчеты средних и погрешностей. Для перехода в статистический режим необходимо нажать кнопки 2ndF+Stat. Как правило, знак Stat стоит над кнопкой включения/сброса ON/C.

После перехода в статистический режим на экране в строке индексов загорается надпись Stat. Теперь можно вводить данные. Для этого надо набрать значение, а затем нажать на кнопку, над которой находится надпись DATA. В ответ на экране загорится номер набранного значения в выборке. После набора всей выборки нажатием кнопки со значком сверху на экран выводится среднее значение, а после нажатия кнопки, над которой написана буква S- среднеквадратичное отклонение. Для расчета погрешности необходимо домножить ее на коэффициент Стъюдента и поделить на корень количества измерений согласно формуле (0.4).

Для выхода из статистического режима надо выключить калькулятор.