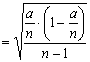 . (4.1.)
. (4.1.)Анализ качественных признаков
Доля и её статистическая ошибка
В
предыдущей главе акцентировалось внимание
исключительно на анализе количественных
признаков, которые часто подчиняются
закону нормального распределения. Наряду с
этим нередки случаи, когда различия между
вариантами изучаемой совокупности
сводятся к качественным признакам. Так,
например, популяцию раздельнополых
организмов можно чётко дифференцировать по
половому признаку и такое разделение будет
вполне информативным, пригодным для
сопоставления. С аналогичной ситуацией
приходится сталкиваться при сравнении
популяций по соотношению выживших и
погибших, доминантного и рецессивного
фенотипа и т.п.
Таким
образом, распределение по качественному
признаку нередко сводится к двум группам:
варианты, являющиеся носителями признака и
варианты не имеющие его. Такое качественное
варьирование называется альтернативным,
поскольку реализация одной из возможных
альтернатив исключает возможность
реализации другой [Федоров,
1957], или биномиальным,
так как формула, описывающая это
распределение, выводится из бинома Ньютона [Павловский,
1967].
Естественное
деление популяции только лишь на две группы
являются частным случаем более общего
явления, когда в анализируемой
совокупности можно выделить несколько
групп, отличающихся по одному
качественному признаку. Общеизвестны,
например, категории цвета глаз и волос у
людей. В среде охотников выделяют “кряжи”,
характеризующие специфику окраса пушного
зверя. Представителей любой популяции
можно подразделить на те или иные
возрастные категории. Однако и в этом, более
общем, случае всё многообразие градаций
качественного признака в конечном счёте
можно свести к двум группам: карие глаза и
не карие, лиса-чернобурка и не чернобурка,
гусеница и не гусеница и т.п.
Для
статистического анализа выборки при
качественном варьировании необходимы
следующие исходные показатели, позволяющие
составить представление о генеральной
совокупности:
n
- число
анализируемых объектов (число наблюдений);
a
- число
объектов, у которых та или иная
альтернатива реализована;
b
- число объектов, у
которых эта альтернатива не реализована.
В
качестве важнейшей описательной
статистики при биномиальном распределении
выступает доля или вероятность,
показывающая относительную частоту
реализованной альтернативы. В книгах по
биометрии доля реализованной альтернативы,
как правило, обозначается символом p,
а противоположенной альтернативы - q.
Доля реализованной альтернативы, какого-либо
признака, находится из соотношения p
= a/n, а доля противоположной альтернативы
соответственно q = b/n
= (1 – p), так как p +
q = 1.
Совершенно
очевидно, что степень надежности
выборочной доли будет возрастать по мере
увеличения числа наблюдений. Поэтому для
корректной оценки параметров генеральной
совокупности обязательно необходимо
определять статистическую ошибку
выборочной доли mp, которая вычисляется по
формуле:
![]()
![]()
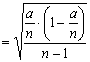 . (4.1.)
. (4.1.)
Алгоритм
оценки разности долей может быть различным,
но в его основой всегда служит t-критерий.
Применимость t-критерия
к анализу альтернативно варьирующих
признаков обусловлена тем, что
биномиальное распределение в пределе
приближается к нормальному [Бейли,
1962; Павловский, 1967 и др.].
Считается, что если в обеих выборках доли не
выходят за границы
![]() оценку можно проводить при помощи t-критерия
обычным способом. Вычисление ведётся по
формуле:
оценку можно проводить при помощи t-критерия
обычным способом. Вычисление ведётся по
формуле:
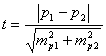 .
(4.2.)
.
(4.2.)
Фактическая
величина t затем
сопоставляется с критическим (табличным)
значением при числе степеней свободы n
= n1 + n2
– 2. При этом, если
![]() выборочные доли
признаются различными, а популяции, откуда
взяты сравниваемые выборки, принадлежащими
к разным генеральным совокупностям.
выборочные доли
признаются различными, а популяции, откуда
взяты сравниваемые выборки, принадлежащими
к разным генеральным совокупностям.
Однако,
когда хотя бы в одной из анализируемых
совокупностей доля не укладывается в
интервал
![]() , формула (4.2.) может привести к ошибочным
результатам, особенно, если объём выборки
недостаточно велик [Плохинский,
1970; Зайцев, 1973 и др.]. В таких случаях более
эффективен метод
, формула (4.2.) может привести к ошибочным
результатам, особенно, если объём выборки
недостаточно велик [Плохинский,
1970; Зайцев, 1973 и др.]. В таких случаях более
эффективен метод
![]() преобразования
Фишера, заключающийся в угловой
трансформации выборочных долей
преобразования
Фишера, заключающийся в угловой
трансформации выборочных долей
![]() [Плохинский, 1972; Рокицкий,
1973; Терентьев, Ростова, 1977 и др.]. Для этого
сравниваемые доли выражают в процентах и
вводят так называемую поправку Йетса на
непрерывность: p1% + 100/(2n1)
и p2% - 100/(2n2).
Затем по специальной таблице (см.
Приложения табл. 2), на основании “исправленных”
поправкой Йетса долей, находят значения
[Плохинский, 1972; Рокицкий,
1973; Терентьев, Ростова, 1977 и др.]. Для этого
сравниваемые доли выражают в процентах и
вводят так называемую поправку Йетса на
непрерывность: p1% + 100/(2n1)
и p2% - 100/(2n2).
Затем по специальной таблице (см.
Приложения табл. 2), на основании “исправленных”
поправкой Йетса долей, находят значения
![]() . Гипотеза о принадлежности выборочных
совокупностей к одной генеральной
совокупности отвергается при выполнении
условия [Лакин, 1990]:
. Гипотеза о принадлежности выборочных
совокупностей к одной генеральной
совокупности отвергается при выполнении
условия [Лакин, 1990]:
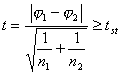 .
(4.3.)
.
(4.3.)
Рассмотрим
сведения В. А. Паевского [1985] о
гибели яиц и птенцов у двух, различных по
плотности гнездования, видов птиц: зелёной
пересмешки Hippolais icternia
Vieill. и зяблика Fringilla
coelebs L. на одном из участков Куршской косы
в 1974-81 гг. (табл. 5).
Таблица
5
Причины
гибели яиц и птенцов у зелёной пересмешки и
зяблика
|
Вид |
Плотность популяции (пар/км2) | Количество гнезд с известной судьбой | Количество разоренных хищниками гнезд | Количество общих потерь (яйца, птенцы) | Количество яиц и птенцов, уничтоженных хищниками |
| Hippolais icternia | 26 | 170 | 45 | 227 | 179 |
| Fringilla coelebs | 218 | 1405 | 396 | 1688 | 976 |
Сопоставим
сначала доли разоренных хищниками гнезд. У
зелёной пересмешки p1 = 45/170
= 0.265 со статистической ошибкой ±
![]() , у зяблика p2 = 396/1405 = 0.282
±
, у зяблика p2 = 396/1405 = 0.282
±
![]() . Так как в обоих случаях p
не выходит за пределы
. Так как в обоих случаях p
не выходит за пределы
![]() трансформации выборочных долей не
требуется. Вставляем полученные значения в
формулу (4.2.):
трансформации выборочных долей не
требуется. Вставляем полученные значения в
формулу (4.2.):
![]() .
.
Вычисленная
величина t уступает
табличным значениям tst = 1.96
(n > 120).
Соответственно отличие в доле разоренных
хищниками гнезд у этих видов несущественно,
что, по мнению В. А. Паевского [1985],
обусловлено очень сходным расположением
гнезд у обоих видов.
Вычисление
долей (и их статистических ошибок)
уничтоженных хищниками яиц и птенцов от
общего количества потерь дало следующие
результаты: зелёная пересмешка p
= 0.789 ±
0.272, зяблик p = 0.578 ±
0.012. Находим фактическую величину t
по тому же алгоритму, что и в приведенном
выше случае (t = 7.07).
Найденная величина превосходит
критическое значение tst = 3.29 (P = 0.999, n > 120),
это означает, что различия долей можно
считать в высшей степени достоверными.
Отсюда
следует, что эти два вида демонстрируют
разные стратегии размножения: на одной и
той же территории, в одних и тех же условиях
размножение одного из них H. icternia – более успешно, несмотря
на то, что доля потерь от главного фактора
гибели гнезд у него выше [Паевский,
1985].
Процедуру
оценки разности долей методом
![]() -преобразования рассмотрим на
гипотетическом примере. Предположим, что у
самки А от самца X приплод составил 8
детёнышей, из которых лишь 1 самец. У самки В,
от того же самца X, родилось 4 детёныша,
причём 2 из них самцы. Исходя из этого можно
предположить, что самка А менее “предрасположена”
к рождению самцов. Выясним, являются ли
такие различия статистически достоверными.
-преобразования рассмотрим на
гипотетическом примере. Предположим, что у
самки А от самца X приплод составил 8
детёнышей, из которых лишь 1 самец. У самки В,
от того же самца X, родилось 4 детёныша,
причём 2 из них самцы. Исходя из этого можно
предположить, что самка А менее “предрасположена”
к рождению самцов. Выясним, являются ли
такие различия статистически достоверными.
Вычисляем
долю самцов в приплоде у первой p1
= 1/8 = 0.125 и второй самки p2 = 2/4
= 0.5. Переводим доли в проценты и вносим
поправку Йетса: p1’ = 12.5 % + 100/ (2×8)
= 18.75% и p2’ = 50.0% -
100/ (2×4)
= 37.5%. По таблице (см. Приложения табл.
2) находим
значения
![]() , соответствующие “поправленным”
долям:
, соответствующие “поправленным”
долям:
![]() 1 = 0.897 и
1 = 0.897 и
![]() 2 = 1.318. Подставляем имеющиеся
значения в формулу (4.3.):
2 = 1.318. Подставляем имеющиеся
значения в формулу (4.3.):
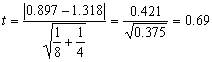 .
.
Фактическая
величина t = 0.69
заметно уступает стандартному значению (tst
= 2.23 и более, так как n
= 10). Это означает, что имеющихся данных явно
недостаточно, для того чтобы статистически
доказать отличия самок по степени “предрасположенности”
к рождению самцов.
Анализ сопряженности признаков и согласованности распределений (хи-квадрат критерий)
Если
совокупность объектов изучается по
нескольким качественным признакам,
зачастую необходимо выяснить, в какой мере
эти признаки являются независимыми друг от
друга. Для этой цели обычно используют
специальный метод, получивший название c2
(хи-квадрат) критерий. В первоначальном виде
он был разработан в 1900 году Пирсоном и
позднее дополнялся многими специалистами (Брандтом,
Снедекором, Фишером, Ястремским и др.).
Для
иллюстрации метода c2
воспользуемся данными о соотношении
окрасочных морф сизого голубя в трех
городах на юге Сибири: Новосибирск, Усть-Каменогорск
и Горно-Алтайск (табл. 6). В ходе сбора
первоначального материала голубей
подсчитывали на разовых маршрутах
приблизительно сходной протяженности. По
окрасу оперения выделены четыре градации.
Две из них (сизая и черночеканная) - типичны
для данного вида, тогда как наличие
непигментированных и красных перьев (пегая
и красная окраска соответственно) для диких
представителей данного вида в целом
несвойственно. В ходе последующего анализа
пегие и красные окрасочные морфы в связи с
их редкостью объединены в одну категорию “нетипичных
фенов”.
Определим,
являются ли классификации популяций по
городам и окрасочным морфам независимыми
или, иными словами, можно ли считать
проанализированные популяции сизых
голубей относящимися к одной генеральной
совокупности. Исходя из общей логики
рассуждения ясно, что если популяции,
обитающие в различных городах, принадлежат
единой совокупности, то доли окрасочных
морф в каждой из них должны быть
относительно постоянными. Отсюда, чем
больше отклонение наблюдаемой частоты от
такого равномерного (“ожидаемого”)
распределения частот, тем больше
вероятность того, что рассматриваемые
популяции отличаются.
На
первом этапе анализа необходимо вычислить
“ожидаемые” частоты, которые находятся
делением произведения двух
соответствующих этой клетки сумм,
записанных по краям таблицы, на сумму всех
наблюдаемых частот. Например, ожидаемое
число нетипичных по окраске голубей в г.
Горно-Алтайске равно
![]() , что заметно больше фактического их числа.
, что заметно больше фактического их числа.
Соотношение
окрасочных морф сизого голубя в некоторых
городах Сибири
|
Город |
Окрасочные морфы |
Всего |
||
| Сизые | Чёрночеканные | Нетипичные | ||
| Новосибирск |
41 (60.5) |
68 (66.3) |
52 (34.2) |
161 |
| Усть-Каменогорск |
50 (57.5) |
74 (63.0) |
29 (32.5) |
153 |
| Горно-Алтайск |
54 (27.0) |
17 (29.7) |
1 (15.3) |
72 |
|
Всего |
145 |
159 |
82 |
386 |
После
нахождения всех ожидаемых частот (в таблице
6 они приведены в скобках) рассчитывается
величина c2,
представляющая собой отношение:
![]() ,
(4.4.)
,
(4.4.)
где
O - наблюдаемые
частоты (англ. observed), E -
ожидаемые частоты (англ. expected).
Вычисленную
таким образом величину c2
сравнивают со стандартными значениями.
Если она превышает то или иное стандартное
значение, исходная гипотеза о
независимости признаков отвергается на
соответствующем уровне вероятности (см.
Приложения
табл. 3).
Как
обычно, при этом необходимо учитывать число
степеней свободы. В случае, когда по каждому
признаку подразделяют не менее трёх
градаций, число степеней свободы находят по
формуле: n = (r
- 1) + (c -1), где r
- число градаций в первой классификации, c
- во второй классификации. Если же одна из
классификаций содержит только две градации,
то n
= (c – 1), где с
– число градаций в более дробной
классификации.
В
нашем примере:
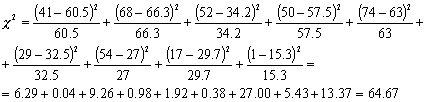
Так
как число степеней свободы здесь равно n
= (3-1) + (3-1) = 4 фактическая величина c2
заметно превосходит все представленные в
таблице критические значения (18.47 и меньше).
Следовательно, рассматриваемые в примере
популяции сизого голубя следует считать
различными по частотному соотношению
окрасочных морф. Нетрудно заметить, что
наиболее существенное отклонение
проявляется в частоте сизой морфы в г. Горно-Алтайске,
наблюдаемая величина которой значительно
превышает ожидаемую.
Таблица
7
Четырехпольная
(2´2)
таблица сопряженности
|
Вторая классификация |
Первая классификация |
Всего |
|
| А | не-А | ||
| В | a | b | a+b |
| не-В | c | d | c+d |
| Всего | a+c | b+d | a+b+c+d=n |
Вычисление
величины c2
упрощается, если исходные данные
сгруппированы в четырехпольную таблицу,
где каждая из классификаций имеет лишь по
две градации. В таких случаях можно
использовать формулы, не требующие
предварительного вычисления ожидаемых
частот, например, следующее отношение (4.5.),
обозначения к которому понятны из таблицы 7:
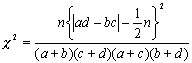 .
(4.5.)
.
(4.5.)
При
изучении независимости классификаций с
помощью четырехпольных таблиц параметр n
равен единице.
В
популяционно-генетических работах, где
оперируют закономерностями Менделя, Харди-Вайнберга
и иными предварительно сформулированными
гипотезами, в сущности, как и при изучении
независимости классификаций, необходимо
сопоставить частоты фактического и
ожидаемого распределения. Достаточно
эффективной статистической основой для
этого также может служить критерий c2
[Хромов-Борисов, 1996].
Рассмотрим
конкретный пример. Л. В. Богданов [1977]
опубликовал результаты изучения фоновой
окраски яиц тонкоклювых кайр Uria
aalge Pontopp., населяющих остров Тюлений (цит.
по: [Кайданов, 1996]). Яйца были
подразделены на три класса: белые (ScW/ScW),
голубые (ScW/ScG)
и зеленые (ScG/ScG).
Окраска яиц детерминируется генотипом
матери.
Подсчет
754 яиц в 1973 году дал следующие результаты:
белые - 115, голубые – 438, зеленые – 201 экз., их
доля составляет 0.1525, 0.5809, 0.2666
соответственно. Отсюда доли аллелей: p(ScW)
= 0.1525 + 0.5809/2 »
0.44; q(ScG) = 0.5809/2
+ 0.2666 »
0.56. Как утверждает закон Харди-Вайнберга
равновесные панмиктические популяции
подчиняются распределению:
p2 + 2pq + q2.
Подставив
имеющиеся значения p(ScW)
и q(ScG)
в формулу получаем, что по Харди-Вайнбергу
ожидаются доли: белые – 0.1936, голубые – 0.4928,
зеленые – 0.3136. Исходя из общего числа
просмотренных яиц (754 экз.) находим
абсолютные частоты: белые – 146, голубые – 372,
зеленые – 236 экз.
Таким
образом, в результате несложных
преобразований получен ряд ожидаемых
частот, пригодный для сравнения с
фактическими частотами методом c2
(табл. 8). Определение величины c2
при этом проводится по формуле (4.4.). В данном
случае необходимо брать лишь одну степень
свободы, поскольку для вычисления
ожидаемых частот достаточно знать долю
лишь одной из аллелей.
Таблица 8
Фактические и ожидаемые частоты яиц тонкоклювой кайр популяции о. Тюленьего в 1973 г.
(данные
Л. В. Богданова [1977])
|
Белые |
Голубые | Зелёные | Всего | |
| Фактическое число | 115 | 438 | 201 | 754 |
| Ожидаемое по Харди-Вайнбергу | 146 | 372 | 236 | 754 |
Так
как c2
= 23.48, а n
= 1 гипотезу о соответствии наблюдаемого в
природе распределения формуле Харди-Вайнберга
можно отвергнуть при высоком уровне
достоверности. Как полагает Л. В. Богданов,
это объясняется тем, что голубая окраска
скоррелирована с лучшей выводимостью и
выживаемостью птенцов, кроме того, она
лучше других обеспечивает маскировку от
основных хищников – крупных чаек.