Анализ многомерных систем
Системой
обычно считается множество элементов,
находящихся в отношениях и связи друг с
другом, образующих определенную
целостность, единство [Энциклопедический
словарь, 2002]. Система не ограничивается
лишь простой суммой элементов, а обладает
более общими свойствами, которые
выражаются в структурированности и
взаимозависимости её частей. Ярким
примером системы, обладающей внутренней (имманентной)
структурой, является организм. Одним из
первых к пониманию этого пришел
французский палеонтолог и сравнительный
анатом Ж. Кювье, ещё в 1806 году
сформулировавший знаменитое правило
корреляции. Согласно этому правилу, все
органы живого организма составляют единую
систему, части которой зависят друг от
друга настолько, что изменение одной из них
влечет за собой изменение другой (цит. по: [Шмидт,
1985]). Более поздние исследования
морфологов позволили существенно
расширить эти представления [Шмальгаузен,
1982; Шмидт, 1985; Берг, 1993; Венгеров, 2001; Terentjev, 1931
и др.]. В частности, показано, что
отдельные части организма нередко образуют
группы, каждая из которых объединяет
признаки, более тесно связанные друг с
другом, нежели с признаками других групп.
Наличие таких групп может быть обусловлено,
например, приспособлениями к полёту,
функциональной дифференциацией отделов
черепа, коэволюционными изменениями у
растений и их опылителей и т.п.
Биологические корреляции могут и не иметь
существенного функционального значения,
как правило, это связано с явлением
плейотропии – способности генов влиять на
развитие более чем одного признака [Майр,
1968; Берг, 1993 и др.].
Сообщества
и, особенно, таксоцены (территориальные
группировки высших систематических
категорий) - менее жёстко взаимосвязанные
системы. Вместе с тем, и они характеризуются
относительно устойчивой структурой. Дело в
том, что, помимо внутренних (трофических,
топических, форических) взаимоотношений,
главнейшая роль в структурированности
территориальных группировок принадлежит
внешним воздействиям, в частности,
комплексу абиотических факторов,
ценотической продуктивности,
антропогенному влиянию и т.п. [Равкин,
1978, 1984; Равкин, Лукьянова, 1976].
Практически
любая система может быть частично отражена
в виде прямоугольной таблицы типа “признаки
´
объекты”. Типичным примером в данном
случае могут служить синэкологические
таблицы, где указывается обилие (или хотя бы
факт присутствия) тех или иных видов в
исследованных местообитаниях; таблицы
результатов морфологических промеров и т.п.
Обозначим матрицу типа “признаки ´
объекты” как первичную s ´ m
матрицу, где s -
признаки (строки) и m -
объекты (столбцы) анализируемой
многомерной совокупности.
Обратимся
к таблице 9, где представлен массив данных,
который формально можно принять за
многомерную систему, состоящую из 4
объектов, характеризующихся 8 признаками.
Пример первичной s ´ m матрицы
| m1 | m2 | m3 | m4 | |
| s1 | 93 | 9.3 | 3 | 9 |
| s2 | 84 | 8.4 | 17 | 27 |
| s3 | 68 | 6.8 | 25 | 88 |
| s4 | 57 | 5.7 | 47 | 51 |
| s5 | 47 | 4.7 | 57 | 75 |
| s6 | 25 | 2.5 | 68 | 24 |
| s7 | 17 | 1.7 | 84 | 22 |
| s8 | 3 | 0.3 | 93 | 38 |
Из
представленной таблицы видно, что объект m1
по всем признакам превосходит объект m2
в десять раз. Эти объекты хотя и не
идентичны, но совершенно определённым
образом связаны между собой, поскольку
степень проявления проанализированных у
объекта m2
признаков прямо пропорциональна их
проявлению у объекта m1
(рис. 6). Объект m3
имеет связь как с m1,
так и с m2,
однако здесь прослеживается уже обратная
зависимость (рис. 7). Заметим, что в этом
случае данные на графике до некоторой
степени отклоняются от “воображаемой”
прямой линии. Это указывает на менее
строгую (стохастическую)
зависимость. Наконец, объект m4, по-видимому,
вообще не связан с объектом m1
(рис. 8) и соответственно с прочими объектами.

Рис.
6. Пример строго
положительной корреляции переменных.
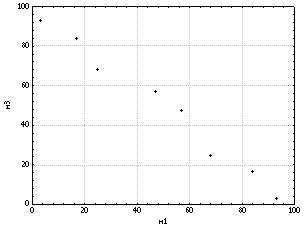
Рис.
7. Пример
отрицательной корреляции переменных.
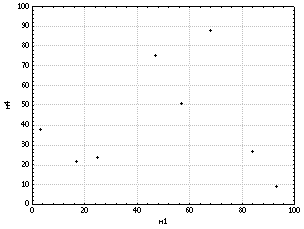
Рис.
8. Пример
отсутствия корреляции между переменными.
Рассмотренные
выше статистические зависимости
называются корреляциями.
Корреляция может быть положительной (при
увеличении одной переменной увеличивается
другая) и отрицательной (увеличение одной
переменной сопровождается уменьшением
другой). Обычно их труднее обнаружить, чем в
приведенном примере, кроме того, для
объективности анализа желательно иметь
показатель степени “согласованности”
переменных. В качестве такой меры чаще
всего используется линейный коэффициент корреляции
Пирсона (r). Он может принимать любые значения
в пределах от –1.00 (строго отрицательная
корреляция) до +1.00 (строго положительная
корреляция). Коэффициент корреляции
определяется формулой:
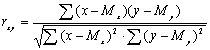 .
(5.1.)
.
(5.1.)
Вычисление
коэффициента корреляции непосредственно
по приведенной выше формуле – трудоёмкая
процедура. Существует несколько более
быстрых способов, использование которых,
кроме того, снижает риск сделать случайную
ошибку [Бейли, 1962; Плохинский, 1970;
Лакин, 1990 и др.]. Алгоритм вычисления
коэффициентов корреляции заложен в
компьютерных программах (Microsoft Excel, STATISTICA, SPSS
и мн. др.). Часть из них стали практически
общедоступными. Достоверность
коэффициента корреляции проще всего
проверить по специальной таблице (см.
Приложения
табл. 4) [Фишер, 1958; Рокицкий, 1973;
Терентьев, Ростова, 1977; Лакин, 1990]. В этой
таблице содержатся критические значения rst
для уровней достоверности P=0.95
и 0.99 с учётом числа степеней свободы n =
n - 2. Если вычисленное значение коэффициента
превышает стандартное значение, корреляцию,
в большинстве случаев, можно считать
достоверной. Необходимо отметить, что этот
способ является довольно приближенным. В
особо ответственных случаях лучше
пользоваться более точным z-преобразованием
Фишера, описание которого можно найти в
более полных руководствах по статистике [Лакин,
1990 и др.].
Среди
специалистов нет единого мнения
относительно преимущества тех или иных мер
связи [Песенко, 1982]. Тем не
менее, совершенно очевидно, что
коэффициенты корреляции и, в том числе,
наиболее обоснованный (с позиций теории
статистики) коэффициент Пирсона пригодны
для использования далеко не во всех типах
исследований. В частности, информативность
коэффициентов корреляции сомнительна в
случае сравнения территориальных
группировок организмов [Песенко,
1982]. В таких исследованиях широкое
распространение получили эвристические (основанные
на общей логике исследования) меры сходства.
Легок в вычислении и, пожалуй, наиболее
широко распространен коэффициент
сходства, впервые использованный в 1901 году
геоботаником П. Жаккаром. Данный индекс
имеет несколько версий и может быть
использован как для сравнения
территориальных группировок организмов по
видовым спискам, так и с учётом их
численности или доли. Индекс Жаккара и его
модификации изменяются в переделах от 0 до 1.
Для идентичных (по сопоставляемым
признакам) объектов он равен 1, для
абсолютно несходных – 0.
Для
сравнения видовых списков формула Жаккара
имеет вид:
![]() ,
(5.2.)
,
(5.2.)
если
сравнение проводится с учётом обилия,
формула трансформируется в следующее
выражение:
![]() ,
(5.3.)
,
(5.3.)
наконец,
при сравнении с учётом долей видов,
входящих в состав группировки:
![]() .
(5.4.)
.
(5.4.)
В
приведённых выше формулах использованы
следующие обозначения: a
– число общих видов в двух сравниваемых
территориальных группировках, b - число видов в первой из
сравниваемых группировок,
c – число видов во второй группировке,
![]() - суммарное обилие в первой из
сравниваемых группировок,
- суммарное обилие в первой из
сравниваемых группировок,
![]() - суммарное обилие во второй группировке,
- суммарное обилие во второй группировке,
![]() - сумма
меньших показателей обилия по всем видам,
свойственным двум сравниваемым
группировкам,
- сумма
меньших показателей обилия по всем видам,
свойственным двум сравниваемым
группировкам,
![]() - сумма
наибольших показателей обилия,
- сумма
наибольших показателей обилия,
![]() и
и
![]() - сумма
наименьших и, соответственно, наибольших
долей видов, в двух сравниваемых
группировках.
- сумма
наименьших и, соответственно, наибольших
долей видов, в двух сравниваемых
группировках.
Существуют
и другие эвристические индексы сходства,
обзор и критический анализ которых можно
найти в обстоятельной монографии Ю. А.
Песенко [1982]. Однако, как
показало экспериментальное сопоставление,
проведенное на обширном материале по
населению птиц южной тайги Западной Сибири,
большинство из предложенных коэффициентов
дают близкие как с формальной, так и с
содержательной точки зрения результаты [Шадрина,
1987]. Отметим, что и коэффициент корреляции,
и коэффициент сходства легко могут быть
представлены в виде меры различия. Для
этого достаточно соответствующим образом
трансформировать коэффициенты:
![]() или
или
![]() , где r’ – мера
различия, основанная на коэффициенте
корреляции Пирсона, I’ – мера различия, основанная на
коэффициенте сходства.
, где r’ – мера
различия, основанная на коэффициенте
корреляции Пирсона, I’ – мера различия, основанная на
коэффициенте сходства.
Помимо
вышеназванных коэффициентов существует
ещё один относительно широко
распространенный тип мер связи - это меры
расстояния (Л1-норма, евклидово
расстояние, расстояние Чебышева и др.).
Применение мер расстояния для анализа
фаунистических данных (в широком смысле)
подробно обсуждается в [Песенко,
1982], там же приводятся формулы для их
вычисления.
Вторичные матрицы и автоматическая классификация
Структурный
анализ многомерной совокупности (отражением
которой является первичная матрица)
целесообразно начинать с построения
вторичных матриц. Вторичная матрица
порядка m ´
m представляет собой
таблицу, в которой содержится
![]() попарных оценок
степени корреляции или сходства
анализируемых объектов. В таблице 10
представлено две вторичных m
´
m матрицы, вычисленные по данным
таблицы 9.
попарных оценок
степени корреляции или сходства
анализируемых объектов. В таблице 10
представлено две вторичных m
´
m матрицы, вычисленные по данным
таблицы 9.
Из
рассматриваемого примера хорошо видно, что
использованные показатели дают
существенно различные результаты.
Последнее закономерно вытекает из их
математических свойств и, во многом,
определяет сферу их применения.
Коэффициенты корреляции, оценивая
сопряженность варьирования объектов, как
правило, вполне информативны в случае
анализа структурированных систем, в
которых превалируют внутренние связи.
Коэффициенты сходства, определяя степень
пересечения признаков, оценивают
абсолютное сходство между объектами и
могут быть полезны для анализа
низкоорганизованных систем, в которых
преобладают внешние ограничения.
Таблица 10
Пример вторичных m ´ m матриц
| m1 | m2 | m3 | m4 | |
| m1 | - | 1 | -0.99 | 0.03 |
| m2 | 0.10 | - | -0.99 | 0.03 |
| m3 | 0.30 | 0.08 | - | -0.01 |
| m4 | 0.51 | 0.12 | 0.47 | - |
В
верхней части таблицы приведены значения
коэффициентов корреляции Пирсона, в нижней
- коэффициентов сходства Жаккара (I2).
Анализ
и интерпретация вторичных матриц может
занимать много времени, особенно если в
сферу анализа задействовано относительно
большое число объектов. Современная
биометрия располагает набором
разнообразных методов, позволяющих заметно
упростить анализ вторичных матриц,
повысить объективность анализа и получить
качественно новую информацию [Василевич,
1969; Андреев, 1980; Шадрина, 1980; Песенко, 1982;
Электронный …, 1999; Гайдышев, 2001; Ефимов, 2003 и
др.].
Широко
распространенным методом упорядочивания
вторичных матриц является метод дендрограмм. Дендрограмма
представляет собой разветвленную
древовидную схему, которая позволяет
выделять наиболее сходные из анализируемых
множеств, представляя их в виде более или
менее изолированных групп или, как их
принято называть, кластеров. Существует
несколько способов построения дендрограмм,
часть из них достаточно подробно описана в
соответствующей литературе [Шадрина,
1980; Песенко, 1982; Мандель, 1988; Электронный …,
1999; Гайдышев, 2001]. Имеется разнообразное
программное обеспечение (STATISTICA, NTSYSpc, BIODIV и
др.), позволяющее обрабатывать данные на
компьютере. Рассмотрим наименее сложный
способ, получивший образное название - “ближайшего
соседа”.
Вторичные s ´ s матрицы
| s1 | s2 | s3 | s4 | s5 | s6 | s7 | s8 | |
| s1 | - | 0.03 | 0.61 | 0.55 | 1.00 | 1.18 | 1.32 | 1.53 |
| s2 | 0.71 | - | 0.44 | 0.36 | 0.77 | 1.05 | 1.21 | 1.39 |
| s3 | 0.40 | 0.58 | - | 0.23 | 0.22 | 1.03 | 1.16 | 1.09 |
| s4 | 0.37 | 0.56 | 0.66 | - | 0.12 | 0.45 | 0.59 | 0.64 |
| s5 | 0.27 | 0.43 | 0.69 | 0.77 | - | 0.44 | 0.53 | 0.45 |
| s6 | 0.20 | 0.37 | 0.33 | 0.54 | 0.56 | - | 0.01 | 0.07 |
| s7 | 0.15 | 0.28 | 0.27 | 0.44 | 0.46 | 0.80 | - | 0.04 |
| s8 | 0.07 | 0.21 | 0.26 | 0.43 | 0.45 | 0.60 | 0.73 | - |
В
верхней части таблицы приведены значения
мер различия (1 – r), в
нижней - значения коэффициентов сходства
Жаккара (I2).
Обратимся
к той части таблицы 11, где представлены меры
различия (1-r),
вычисленные по данным первичной матрицы
порядка s ´
m (табл. 9). Заметим, что в качестве
анализируемых объектов здесь выступают
строки (но не столбцы) первичной s ´ m матрицы. Находим наиболее сходные
множества, различие между которыми
минимально. В данном примере это s6
и s7 (1 – r)
= 0.01. Эти множества изображаются на графике
соседними точками на одной из осей.
Отходящие от точек параллельные линии
соединяются перпендикулярным отрезком на
данном уровне расстояния, который
откладывается на другой оси двумерной
координатной сетки. Так, на рисунке 9 на
оси ординат положены объекты, а на оси
абсцисс приведена линейная шкала значений
мер расстояния. Следующая по силе связь
прослеживается между множествами s1
и s2 (0.03). Затем
идёт связь между s8
и s7 (0.04).
Несмотря на то, что множество s7
уже образует группу с s6,
по алгоритму “ближайшего соседа” s8
включается в состав этой группы и т.д.
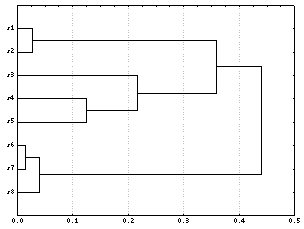
Рис.
9. Пример дендрограммы, построенной на
основе матрицы мер различия (1–r)
методом “ближайшего
соседа”.
Другим средством, позволяющим упорядочить вторичную матрицу, является метод корреляционных плеяд, в первоначальном виде предложенный П. В. Тереньтевым [1959, 1960; Терентьев, Ростова, 1977].
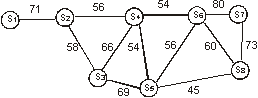
Рис.
10. Пример
неориентированного графа сходства,
построенного на основе матрицы
коэффициентов Жаккара. Порог
сходства равен 45 % (средний уровень
сходства во вторичной матрице).
Суть
данного метода состоит в построении графов,
то есть схем, где объекты изображены в виде
точек (или других значков), часть из которых
соединяется линиями - рёбрами графа. При
этом рёбра графа соединяют только те
объекты, связь между которыми превосходит
заранее определенный порог сходства.
Степень соответствия между объектами, как
правило, отражается характером взаимного
расположения точек, то есть чем больше
уровень сходства или корреляции между
объектами, тем ближе на графе они
расположены друг к другу. Иногда отличия в
уровне связи показывают при помощи толщины
рёбер графа и т.п. На рисунке 10 в качестве
примера представлен граф сходства,
построенный на основе вторичной s ´ s матрицы коэффициентов сходства
Жаккара (табл. 11).
Более
информативным, по сравнению с обычным типом
графа, является ориентированный граф.
Подобные графы могут быть очень полезны при
изучении географической изменчивости
организмов. Однако наибольшее
распространение они нашли в факторной
зоогеографии, развиваемой научной школой Ю. С.
Равкина [Равкин, 1978, 1984, 2002;
Равкин, Лукьянова, 1976; Вартапетов, 1984; Равкин
и др., 2003 и мн. др.]. Ориентированный граф
отражает не только характер проявляющихся
у анализируемых объектов связей, но и
показывает предметно интерпретируемые
векторные направления (тренды), а также
отклонения от них. Применительно к
территориальным группировкам животных в
качестве маркеров направленных изменений
выступают физиономические,
гидротермические и иные свойства
населяемых этими группировками биотопов.
Если анализируется небольшой объём данных
ориентированный граф можно строить
непосредственно по исходной матрице
коэффициентов сходства (корреляции). Однако,
как правило, построению графа предшествует
генерализация исходной многомерной
системы, выражающаяся в объединении
исходного множества в более или менее
однородные группы. Для этой и других целей
разработан пакет программ Jacobi,
включающий ряд специальных и традиционных
методов многомерной статистики [Ефимов,
2003].
Он доступен вкладчикам Банка данных
лаборатории зоологического мониторинга
ИСиЭЖ СО РАН.
Пример ориентированного графа, представляющего модель пространственной структуры населения дневных бабочек Северо-Восточного Алтая, приводится на рисунке 11. Схема построена по результатам факторной классификации [Куперштох, Трофимов, 1975].
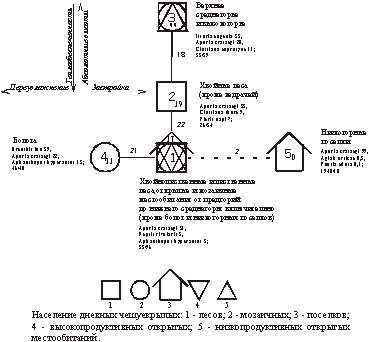
Рис.
11. Пространственная
структура населения дневных бабочек Северо-Восточного
Алтая.
Цифры
внутри значков – номера классов, индексы
под ними – уровень внутриклассового
сходства, цифры у связующих линий – уровень
межклассового сходства. Сплошные линии -
значимое сходство, штриховые – запороговое.
Для каждого класса указано три первых по
долевому участию вида, суммарное обилие (особей/га)
/ число видов.
На графе достаточно четко прослеживается связь облика населения дневных бабочек с теплообеспеченностью (классы 1 - 3), что проявляется, в частности, в своеобразии населения хвойных лесов (класс 2). Заслуживает внимания промежуточное положение этого класса, выступающего в качестве переходного между населением высокогорий и подгольцовых среднегорий (класс 3) с одной стороны, а с другой стороны - остальных местообитаний Северо-Восточного Алтая (класс 1). Сообщества дневных бабочек на болотах формируются в условиях постоянной переувлажнённости и потому отклоняются от основного вектора (класс 4). Ещё более специфично население низкогорных поселков (класс 5). Оно состоит почти исключительно из боярышницы Aporia crataegi L., прилетевшей сюда в поисках дополнительного минерального питания.
Наряду
с классификационными методами для анализа
многомерных систем зачастую применяется
ординация. Первые исследования с её
применением осуществлены геоботаником Л. Г.
Раменским ещё в первой трети XX века [Шварц,
Шефтель, 1990]. Подавляющее же большинство
ординационных методов предложены во второй
половине прошлого века.
Подробное
рассмотрение методов ординации (как
впрочем и современных методов
классификации) совершенно не возможно без
знания основ линейной алгебры. Существует
ряд доступных учебников по этому
направлению [Баврин, 2002 и др.].
Остановимся
лишь вкратце на одном из наиболее известных
методов: анализе главных компонент.
Последний не изменяет в ходе обработки
расстояния между объектами и
соответственно не искажает содержательный
смысл получаемых результатов [Ефимов,
2003]. Модули расчёта главных компонент
имеются в статистических программах (STATISTICA,
SPSS, NTSYSpc, Jacobi
и др.). Компонентный анализ направлен на
решение следующих задач:
·
снижение
размерности признакового пространства
путём перехода к новым признакам - главным
компонентам;
·
выявление и
изучение статистической связи признаков с
главными компонентами;
·
группировка
объектов в многомерном пространстве.
Главных
компонент столько же, сколько признаков в
первичной s ´ m матрице. Первая главная компонента
обладает максимальной дисперсией из всех,
которые могут быть получены линейным
преобразованием данных, вторая -
максимальной дисперсией из ортогональных к
первой компоненте и т. д. Обычно первые 2-5
главных компонент с достаточной полнотой
(70-90 %) исчерпывают всю дисперсию исходной
матрицы. Последующий анализ сводится к их
предметному объяснению, что достигается
путём изучения вкладов первоначальных
признаков. Заметим, однако, что главные
компоненты не всегда могут быть
содержательно интерпретированы.
Матрица собственных векторов (матрица факторных нагрузок)
| Выборка | I-ГК | II-ГК | Выборка | I-ГК | II-ГК |
| Майма_1 | 0.18 | 0.14 | Онгудай_1 | 0.19 | -0.15 |
| Майма_2 | 0.18 | 0.20 | Онгудай_2 | 0.19 | 0.08 |
| Майма_3 | 0.19 | 0.03 | Онгудай_3 | 0.15 | 0.57 |
| Чемал_1 | 0.18 | 0.22 | Усть_Кокса_1 | 0.19 | 0.13 |
| Чемал_2 | 0.17 | 0.27 | Усть_Кокса_2 | 0.18 | 0.20 |
| Чемал_3 | 0.17 | 0.33 | Усть_Кокса_3 | 0.19 | 0.07 |
| Чоя_1 | 0.19 | -0.10 | Усть_Кан_1 | 0.18 | -0.18 |
| Чоя_2 | 0.19 | -0.14 | Усть_Кан_2 | 0.18 | -0.17 |
| Чоя_3 | 0.19 | 0.05 | Усть_Кан_3 | 0.18 | -0.17 |
| Турачак_1 | 0.19 | 0.001 | Улаган_1 | 0.18 | -0.18 |
| Турачак_2 | 0.19 | -0.02 | Улаган_2 | 0.19 | -0.09 |
| Турачак_3 | 0.19 | 0.02 | Улаган_3 | 0.19 | -0.12 |
| Шебалино_1 | 0.19 | -0.09 | Кош_Агач_1 | 0.18 | -0.19 |
| Шебалино_2 | 0.19 | -0.14 | Кош_Агач_2 | 0.18 | -0.19 |
| Шебалино_3 | 0.19 | 0.0009 | Кош_Агач_3 | 0.18 | -0.19 |
Для
иллюстрации метода воспользуемся данными
за 2001-03 гг. об уровне заболеваемости
глистными инвазиями и лямблиозом “групп
риска” в Республике Алтай (сведения
предоставлены санитарно-эпидемиологической
станцией РА). В качестве объектов в этом
случае удобно рассматривать заболевания, а
в качестве признаков – сведения по районам
и по годам. Расчёт собственных чисел
показал, что первая компонента снимает 95.5 %
исходной дисперсии матрицы. Учитывая, что
все признаки вошли в первую компоненту с
положительным вкладом (табл.
12), можно предположить, что она является
отражением общей изменчивости в уровне
заболеваемости. Заметим также, что
энтеробиоз и аскаридоз расположились в
области положительных значений первой
главной компоненты, а остальные
заболевания - в области отрицательных (табл.
13). Это хорошо согласуется с тем, что
аскаридоз и особенно энтеробиоз
встречаются значительно чаще других
инвазий и оба этих заболевания
зарегистрированы почти во всех
обследованных местностях.
Во
вторую главную компоненту, которая снимает
3.3 % дисперсии, с устойчивым положительным
вкладом входят выборки из Майминского,
Чемальского и Усть-Коксинского
района, а с отрицательным – Усть-Канского,
Улаганского и Кош-Агачского. Вклад выборок
из остальных районов изменяется по годам и,
как правило, относительно не велик (табл.
12). Сравнение условий проживания в
названных районах свидетельствует о связи
уровня заболеваемости с природными
условиями. В частности, Усть-Канский,
Улаганский и особенно Кош-Агачский районы
характеризуются холодными и сухими зимами.
Здесь складывается исключительно
неблагоприятная обстановка для
распространения аскарид, на что указывает
положение аскаридоза в области
положительных значений второй главной
компоненты, но в этих районах относительно
высокий уровень зараженности прочими
глистными инвазиями.
Положение объектов (заболеваний) в пространстве I и II главных компонент
| Заболевание | I-ГК | II-ГК |
| Аскаридоз | 0.29 | 0.88 |
| Энтеробиоз | 4.96 | -0.17 |
| Тениаринхоз | -0.79 | -0.17 |
| Гименолипидоз | -0.79 | -0.11 |
| Описторхоз | -0.73 | -0.13 |
| Трихоцефалез | -0.81 | -0.18 |
| Тениоз | -0.82 | -0.18 |
| Эхинококкоз | -0.78 | -0.14 |
| Лямблиоз | -0.53 | 0.21 |
Оценка силы воздействия факторов
Методы
автоматической классификации и ординации
позволяют получить представление о том,
какие внутренние и внешние факторы
оказывают наиболее значимое воздействие на
систему. Однако иерархия факторов (их ранги
по уровню воздействия на систему) при этом
остаётся до конца не выясненной. Так,
например, по результатам анализа главных
компонент можно с уверенностью судить лишь
об очень ограниченном числе факторов,
которые объясняют наибольшую часть
изменчивости в системе. По результатам
автоматической классификации зачастую
удаётся выяснить действие большего числа
факторов, но вопрос об их ранжировке при
этом либо вообще не ставится, либо её
проводят исходя из концептуальных,
интуитивных или устоявшихся в той или иной
науке положений.
Считается,
что наиболее обоснованные выводы об
иерархии организующих факторов могут быть
получены методами множественной регрессии [Электронный
…, 1999]. Основное
препятствие для широко внедрения
названного метода состоит в том, что он
требует количественных оценок факторов.
Так, например, в случае анализа
закономерностей пространственного
размещения сообществ для этого необходимы
количественные данные о температуре,
влажности и иных характеристиках среды во
всех обследованных местообитаниях. На
практике же биолог, в лучшем случае,
располагает сведениями из окрестных
метеостанций или мелко- и
среднемасштабными картами.
Преодолеть
указанные затруднения позволяет
качественная линейная аппроксимация –
метод, предложенный математиками В. Л.
Куперштохом и В. А. Трофимовым [Равкин,
1978].
Расчёты по этому методу ведутся на основе
вторичной матрицы коэффициентов сходства (или
корреляции) и матрицы значений факторов.
Значения факторов задаются экспертно в
номинальной шкале. Например, характер
увлажненности территории может быть
представлен градациями: болота,
полузаболоченные или влажные территории и
суходолы. Матрица факторов среды строится в
0-1 виде, где каждому объекту присваивается
качественное значение фактора.
Аппроксимация может проводиться по
нескольким факторам одновременно. В
качестве меры для оценки силы влияния
отдельного фактора на систему принимается
изменчивость, которую снимает
этот фактор во вторичной матрице
коэффициентов. Выражением её является
дисперсия или коэффициент регрессии.
Программное обеспечение метода
реализовано в пакете статистических
программ Jacobi
[Ефимов, 2003].
В
качестве примера использования метода
качественной линейной аппроксимации
приведём завершающий этап анализа
пространственного распределения бабочек Hesperiidae
Latr. на Алтае. Первый
этап исследования включал в себя сбор
количественных данных об обилии этих
бабочек в основных ландшафтных урочищах
физико-географических провинций. Затем
методом автоматической классификации [Куперштох,
Трофимов, 1975]
проведена иерархическая группировка, в
результате которой виды объединялись в
сходные по характеру распределения группы.
Кроме того, виды классифицировались по
ареалам с учётом широтной и долготной
составляющих [Сергеев,
1986].
Каждый из выше названных подходов позволил
с различных сторон охарактеризовать объект
исследования. Однако в итоге осталось не
ясным в какой мере стациальное
распределение Hesperiidae
на Алтае согласуется с их глобальным
распределением (ареалом). Для решения этой
задачи понадобилось оценить
информативность выявленных характеристик.
Наиболее
информативной, как и следовало ожидать,
оказалась классификация по сходству
стациального распределения. Даже на уровне
типа она снимает около 59 % дисперсии (табл.
14). Отношение к широтным ареалогическим
рубежам заметно менее информативная
характеристика, что свидетельствует об
определенном несоответствии распределения
в глобальном и региональном масштабе. Ещё
менее четко проявляется совпадение в
пространственном распределении на Алтае у
видов, сходным образом реагирующих на
долготные географические рубежи. Наконец,
филогенетическое родство, определяемое как
принадлежность к подсемейству Pyrginae
или Hesperiinae,
фактически
не оказывает сколько-нибудь существенного
влияния на распределение видов. Эта
характеристика аппроксимируется лишь на
уровне “шума”.
Информативность проанализированных характеристик толстоголовок Алтая
| Характеристика | Снятая дисперсия |
| Подтип стациального распределения | 65 |
| Тип стациального распределения | 59 |
| Широтная ареалогическая группа | 23 |
| Долготная ареалогическая группа | 13 |
| Филогенетическое родство | 5 |
| Сочетание характеристик | 85 |