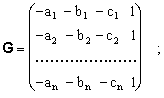
10. АНАЛИТИЧЕСКИЕ РЕШЕНИЯ ПРИ АБСОЛЮТНЫХ ОПРЕДЕЛЕНИЯХ
Решение линейной пространственной засечки. В вычислениях используют измеренные псевдодальности
Pi = Ri + DАП + еi (i = 1,..., n),
где P - псевдодальность, R - геометрическая дальность, DАП - искажения дальности R в пункте наблюдений, е - влияние всех остальных погрешностей, которые в данном случае рассматриваем как случайные, i - текущий номер наблюдаемого спутника, причем nі4. Представим искомые координаты в виде:
X = Xo + x, Y = Yo + y, Z = Zo + z,где Xo, Yo, Zo - известные приближенные значения координат, x, y, z - поправки в приближенные координаты. Именно эти поправки предстоит найти. Геометрическая дальность до i-го спутника
Ri = [(Xi-Xo-x)2 + (Yi-Yo-y)2 + (Zi-Zo-z)2]1/2 .Преобразуем данное выражение следующим образом:
Ri = Roi [1 -2(aix + biy + ciz)/Roi + (x2 + y2 + z2)/Roi2]1/2,
где обозначенно через
Roi = [(Xi-Xo)2 + (Yi-Yo)2 + (Zi-Zo)2]1/2 ,ai = (Xi-Xo)/Roi, bi = (Yi-Yo)/Roi, ci = (Zi-Zo)/Roi.
Выражение в квадратных скобках в правой части формулы для Ri разложим в ряд Тейлора, ограничиваясь только линейной частью ряда:
[1 - t]1/2 = 1 - t/2 + ...
Это сделать возможно:
поправки в координаты малые величины и всеми
членами, содержащими x/Roi, y/Roi,
z/Roi в степенях
выше первой, можно пренебречь.
Чтобы ослабить влияния погрешностей е, исправим
измеренные псевдодальности поправками v.
Поправки будем искать по методу наименьших
квадратов. Для простоты рассуждений примем, что
все псевдодальности измерены с одинаковой
точностью. Решение по МНК выполняется под
условием минимума суммы квадратов поправок:
Sv2 = min.
Тогда для уравнения i-ой поправки можно
записать:
где li,=Рi+Roi зависит от результата измерений Рi.
Выделим матрицы и векторы утолщенными буквами:
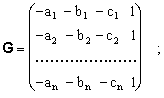
V=(v1, v2,..., vn)т;
U=(x, y, z, DAI)т; l=(l1, l2,...,
ln)т.
Для системы уравнений поправок имеем:
V = GU - l .Как известно, решение по МНК приводит к условию GтV = 0. Отсюда получаем систему нормальных уравнений, решая которую определяем искомые параметры U:
GтGU = Gтl и U = (GтG)-1 GтlОбратим внимание на следующее. Матрица G зависит от приближенных значений координат Xo, Yo, Zo , которые должны быть известны. Поэтому решение линейной засечки по псевдодальностям выполняется последовательными приближениями, уточняющими значения искомых параметров U.
Геометрический фактор. Система нормальных уравнений имеет решение, если определитель матрицы ее коэффициентов GтG не равен нулю:
det(GтG) /= 0 . Чем
больше определитель отличается от нуля, тем
лучше линейная засечка и тем точнее решение. В
этом проявляется суть геометрического фактора
засечки.
Важно выяснить, при каких обстоятельствах
засечка плохая или даже совсем нет решения. Это
можно наглядно показать для случая, когда нет
избыточных измерений и когда четыре параметра x,
y, z и DАП
определяют по наблюдениям только четырех
спутников. Тогда
Решения не будет, когда матрица G выражена и определитель det(G)=0. Посмотрим, когда это произойдет. Допустим, что дальности до спутников одинаковы и все Roi = Ro. Как известно, множитель, общий элементам какого-либо столбца (строки), можно вынести за знак определителя. Получаем:
det(G) = - (1/Ro3) W ,где
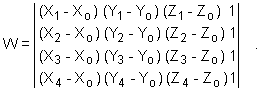
В правой части под
знаком определителя находятся координаты
четырех спутников. Начало счета координат
перенесено в определяемый пункт. Как известно, в
такой записи определитель W равен шестикратному
объему треугольной пирамиды, в вершинах которой
расположены эти четыре спутника. Отсюда ясно, что
определитель det(G) тем больше, чем больше
объем этой пирамиды. Вероятно, объем будет
наибольшим, когда три спутника расположатся в
плоскости горизонта в вершинах равностороннего
треугольника, в центре которого находится
наземная определяемая станция, а четвертый
спутник будет в зените над станцией. Практически
такой случай невозможен, ибо спутники наблюдают
лишь тогда, когда они над горизонтом не ниже 10°.
С другой стороны W = 0 означает,
что все четыре спутника лежат в одной плоскости.
Однако, не следует забывать, что определитель W
записан при допущении, что расстояния от станции
до спутников одинаковы. Поэтому в
действительности определитель станет равным
нулю, когда все КА окажутся в плоскости основания
прямого кругового конуса, вершина которого в
наблюдаемом пункте. В этом
случае линейная засечка решения не имеет.
Решение будет тем хуже, а геометрический фактор
тем больше, чем ближе спутники к одной плоскости.
Практически при наблюдении четырех спутников 1,6
<ГФ < бесконечности (Алексеев, 1993). В измерения
следует включать не четыре, а все видимые на
допустимой высоте над горизонтом спутники.
Оценка
геометрического фактора. Чтобы
понять, как вычисляют ГФ, ознакомимся с
некоторыми положениями оценки точности
измерений при обращении к МНК. Вектор параметров U = (x, y, z, DАП)т вычислен
по данным вектора измерений l
= (l1, l2,..., ln)т.
Его элементы содержат случайные погрешности.
Точность вектора характеризует симметричная
ковариационная матрица Kl. Верхняя ее часть имеет вид:
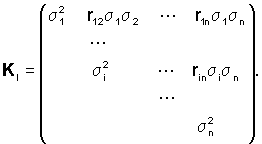
На главной
диагонали расположены дисперсии погрешностей
величин li. Недиагональные элементы на
пересечении i-ой строки (столбца) и j-го столбца
(строки) определяют корреляционные связи и
коэффициент корреляции rij погрешностей в величинах li и lj. Для
равноточных и некоррелированных n величин, когда
недиагональные элементы нули, все s2 одинаковы
и равны дисперсии m2, характеризующей
точность измерений псевдодальностей, E -
единичная матрица с n единицами на главной
диагонали, ковариационная матрица принимает
простой
вид:
K l = m2E
В общем случае задача по нахождению ковариационной матрицы может быть сформулирована следующим образом. Случайный вектор Y (вектор, отягощенный случайными погрешностями) вычисляется через другой случайный вектор l, ковариационная матрица которого K l , по формуле
Y = Al + bгде матрица A и вектор b имеют
постоянные элементы. Тогда ковариационная
матрица
K у вектора Y будет иметь вид:
Ky = AKlAт
По этой формуле для
ковариационной матрицы Ku вектора U в случае равноточных и
некоррелированных измерений получают:
Ku = m2Q, где Q = (GтG)-1.
Для дисперсии si2 i-го элемента вектора U имеем:
si2 = m2Qii ,
где Qii - диагональный элемент матрицы Q, расположенный на
пересечении ее i-х строки и столбца.
Соответственно для СКП координат х, у, z,
являющихся первыми тремя элементами вектора U,
имеем:
Точность положения точки в трехмерном пространстве характеризуют средней квадратической погрешностью положения, вычисляемой по формуле
sp = (sx2 + sy2 + sz2)1/2 или sp = m (Q11 + Q22 + Q33)1/2 .
Пользователя чаще интересует смещение определяемого пункта не в трехмерном пространстве, а на земной поверхности. Если точка сдвигается в трехмерном пространстве по координатным осям на величины x, y, z, то это приводит к изменению геодезических широт, долгот и высот на величины dB, dL, dH и смещению точки вдоль меридиана на отрезок m, перпендикулярно меридиану на отрезок n, а по высоте на величину h. При этом
m = (M + H)dB, n = (N + H)cosB dL, h = dHгде М и N - радиусы кривизны соответственно меридиана и первого вертикала земного эллипсоида. Обозначим через V = (m, n, h, DAI)T. Связь между векторами U и V будет:
V = ФU.
Эта
формула показывает, как смещения в трехмерном
пространстве влияют на сдвиг в
горизонтальной плоскости на некоторой высоте Н
над эллипсоидом. Матрица Ф имеет вид:
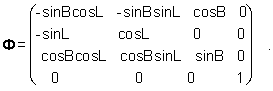
Для ковариационной матрицы Г вектора V и дисперсий элементов этого вектора si2 получаем:
Г= m2 ФQФT, si2 = m2 Гii.
Соответственно для СКП смещений вдоль меридиана, перпендикулярно ему и вверх по вертикали имеем:
sm = mДля СКП положения точки в горизонтальной плоскости и в пространстве получим:
sг = m (Г11 +Г22)1/2,s
p = m (Г11 + Г22 + Г33)1/2.Геометрический фактор определяется соотношением:
ГФ = si /mСоответственно тому, какие использованы si, будут определены разные составляющие ГФ. Обычно оценивают ГФ положения точки в пространстве (sp), на горизонтальной плоскости (sr) и по высоте (sh). Часто встречается ГФ в английской аббревиатуре:
G
DOP = (Q11 + Q22 + Q33 + Q44)1/2 = (Г11 + Г22 + Г33 + Г44) 1/2,PDOP = (Q11 + Q22 + Q33)1/2 = (Г11 + Г22 + Г33) 1/2,
HDOP = (Г11 + Г22) 1/2,
VDOP =
T
DOP =DOP (Dilution of Precision) - обозначает уменьшение точности; первые буквы G (Geometrical - все составляющие), P (Position - положение в пространстве), H (Horizontal - на горизонтальной плоскости), V (Vertical - по высоте), T (Time - во временных задержках) говорят, о каком уменьшении точности идет речь. ГФ становится меньше при наблюдении более 4 спутников. Основным показателем ГФ является PDOP. Для оценки качества засечки пользуются следующей шкалой:
| PDOP | Вербальной оценка |
| <4 | Хорошо |
| 5-7 | Удовлетворительно |
| >7 | Плохо |
Распределения геометрического фактора.
Изучены частоты w распределения геометрического
фактора на земном шаре (Алексеев, 1993).
Моделировали местоопределения в течение суток с
интервалом 0,5 часа в точках поверхности
Северного полушария, расположенных через 3° по
широте и 3°/cosB по долготе. Рельеф учитывали по
карте масштаба 1:100 000. Часть результатов
исследований отражена на диаграммах рис. 19. На
открытой местности геометрический фактор
изменяется в пределах: 1,6 < ГФ < бесконечности.
Диаграммы рис. 19а показывают в процентах
возможность позиционирования, когда ГФ < 4, 7 и 10
и когда в наличии разное количество КА. Как видно,
24 спутника на открытой местности обеспечивают
надежное определение координат. При уменьшении
числа спутников до 18 точность падает, а
местоопределения при ГФ < 4 возможны менее
чем в 70% случаев. После отключения половины (12)
спутников нарушается непрерывность определений,
ГФ > 10, местоопределения с высокой точностью
становятся невозможными, а в 50% случаев задача не
имеет решения.
Надежные определения имеют место при углах
закрытия горизонта 100. С увеличением этих углов
точность определений понижается. При углах 30°
маловероятны ГФ < 4 и определения с высокой
точностью практически не возможны; при углах 40°
задача решения не имеет (рис. 19б). В горной
местности из-за больших углов закрытия горизонта
условия позиционирования ухудшаются. Так,
точность в Карпатах может снизиться в два-три
раза, а на Военно- Грузинской дороге - еще больше
(рис. 19в).
На широтах менее 200 и
высотах над горизонтом выше 300 имеет место
практически нулевая вероятность наблюдений
более 4 ИСЗ (Акимов, Кузьмин, 1996).
В GPS обращение спутников синхронно с вращением
Земли, поэтому в определенных точках земной
поверхности в одно и то же время суток КА создают
одинаковый геометрический фактор.
Образуются области с пониженными значениями ГФ.
Этого недостатка нет в ГЛОНАСС, где выбранная
высота орбиты создает непрерывное изменение
конфигурации созвездий КА над одним и тем же
географическим местом для одного и того же
времени, периодически повторяясь через каждые 7
суток (Салищев, 1995).
Совместное использование созвездий ГЛОНАСС и GPS
гарантирует как минимум 4 спутника, находящихся
над горизонтом выше 300 (Акимов, Кузьмин, 1996).
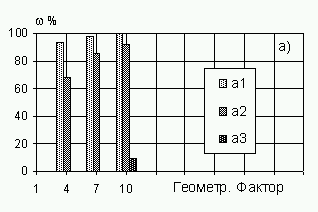

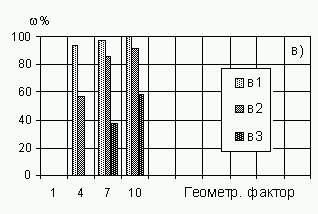
Рис. 19.
Распределения геометрического фактора в
различных ситуациях позиционирования
а) на открытой местности при 24 (а1), 18 (а2) и 12 (а3)
спутниках;
б) для углов закрытия горизонта 10° (б1), 20°(б2), 30°
(б3), 40° (б4);
в) на дорогах Санкт-Петербург-Кингисепп (в1),
Мукачево-Черновцы (в2), Военно-Грузинской (в3)
Дифференциальные поправки в псевдодальности. Поправки формируют на базовой станции A сравнением геометрических дальностей RAi , вычисляемых по координатам наземной станции и i-го спутника, с измеренными псевдодальностями PAi.
PAi = RAi + DAПA + dКAi + eAi,
где DAПA, dКAi, eAi искажения, внесенные соответственно станцией A, спутником i и прочими источниками. Для поправки запишем:
D PAi = RAi - PAi = - DAПA - dКAi - eAi.Важно, что поправки - малые величины и удобны для трансляции. На станции B исправленная псевдодальность ` PBi все еще содержит аппаратурные задержки и остатки прочих искажений:
PBi = PBi + D PAi = RBi + (DAПB - DAПA) + (eBi - eAi).Для уравнения i-ой поправки, как и в случае решения линейной пространственной засечки в автономном режиме (см. начало раздела 10), получим:
vi = - aix - biy - ciz + (DAПB - DAПA) - li,где li = PBi - RОBi, RОBi - приближенное значение RBi, x, y, z - поправки в приближенные
координаты станции B. Чтобы найти четыре
неизвестные величины - x, y, z и (DAПB
- DAПA), нужно отнаблюдать не
менее четырех спутников.
Дифференциальные поправки в фазовые дальности.
На базовой станции A по наблюдениям i-го спутника
определена часть фазовой дальности, которую
представим в виде:
где PAi - геометрическая дальность от станции до
спутника, NAi -
неизвестное число
неоднозначности, dКAi , DAПA, eAi - искажения, внесенные
аппаратурой спутника, наземной станции и прочими
источниками. Используя кодовые измерения и
геометрические дальности, можно оценить число
неоднозначности. Пусть этой оценкой будет целое
число КAi . В общем
случае КAi не
равно NAi. Фазовую
дальность приближенно можно представить в виде:
Тогда для дифференциальной поправки, которая будет малой величиной, получим:
D PAi = RAi - P'Ai = RAi - dPAi - KAi l .Подставив значение dPAi будем иметь:
D PAi = (NAi - KAi) l - dКAi - DAПA - eAiНа подвижной станции В исправленные результаты измерений dPВi имеют вид:
dPBi = dPBi + D PAi = RBi - (NBi - NAi + KAi) l + (DAПB - DAПA) + (eBi - eAi).Отсюда, для уравнения i-ой поправки получаем:
vi = - aix - biy - ciz - NABi + (DAПB - DAПA) - li,где NABi = (NBi - NAi + KAi), li = ` dPBi - ROBi, ROBi - приближеннок значение RBi. Следовательно, предстоит найти поправки х, у, z, в приближенные координаты станции В, аппаратурные искажения (DAПB - DAПA) и определить методом OTF целое число NABi