Решение задач - это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придется работать, те инструменты, с помощью которых выполняется эта работа.
Значит, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач.
Начнем все это изучать.
Итак, что же такое задача?
Если приглядеться к любой задаче, то увидим, что она представляет собой требование или вопрос, на который надо найти ответ, опираясь и учитывая те условия, которые указаны в задаче.
Поэтому, приступая к решению какой-либо задачи, надо ее внимательно изучить, установить, в чем состоят ее требования (вопросы), каковы условия, исходя из которых надо решать задачу. Все это называется анализом задачи. Вот и начнем учиться производить анализ задачи.
Получив задачу, мы, естественно, ее внимательно читаем.
3адача 1. В прямоугольном, треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 см и 12 см. Найти катеты треугольника.
Первое, что мы можем заметить при чтении этой задачи, состоит в следующем: в ней имеются определенные утверждения и требования. В ней утверждается, что "в прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 см и 12 см". Требование задачи состоит в том, что нужно <найти катеты треугольника>найти катеты треугольника.
Часто требование задачи формулируется в виде вопроса. Но всякий вопрос предполагает требование найти ответ на этот вопрос, а поэтому всякий вопрос можно заменить требованием.
Как видим, формулировка любой задачи состоит из нескольких утверждений и требований. Утверждения задачи называются условиями задачи.
Отсюда ясно, что первое, что нужно сделать при анализе задачи,- это расчленить формулировку задачи на условия и требования. Заметим, что в задаче обычно не одно условие, а несколько независимых элементарных (т.е. нерасчленимых дальше) условий; требований в задаче также может быть не одно. Поэтому необходимо расчленить все утверждения и требования задачи на отдельные элементарные условия и требования.
В задаче 1 можно вычленить такие элементарные условия:
1) треугольник, о котором идет речь в задаче, прямоугольный;
2) в этот треугольник вписана окружность;
З) точка касания окружности с гипотенузой делит ее на два отрезка;
4) длина одного из этих отрезков равна 5 см;
5) длина другого отрезка равна 12 см.
Требование этой задачи можно расчленить на два элементарных:
1) найти длину одного катета треугольника;
2) найти длину другого катета треугольника.
Расчленение формулировки задачи на условия и требования не всегда легко произвести. В ряде случаев для этого нужно переосмыслить задачу, переформулировать ее. Например.
Задача 2. Сколько цифр содержит число 2100 (в десятичной системе счисления)?
Формулировка этой задачи состоит из одного вопроса. Но, вдумавшись в этот вопрос, мы можем из него вычленить такие условия:
1) 2100 есть натуральное число;
2) его можно записать обычным образом в виде многозначного числа в десятичной системе счисления.
Тогда требование этой задачи состоит в следующем: найти, сколько цифр содержит запись этого многозначного числа.
Задача 3. Решить уравнение ax2- x3+ a2x - a = 0
Формулировка этой задачи состоит из одного требования. Но анализ этого требования позволяет вычленить из него условие и собственно требование. Условие: ax2- x3 + a2x - a =0 есть уравнение, а требование: решить это уравнение.
Конечно, на этом нельзя остановиться и надо продолжить анализ. Мы замечаем, что запись уравнения содержит две буквы: а и х. Предполагается, конечно, что вы знаете, что эти буквы обозначают: буква а- параметр, т. е. величину, которая в пределах данной задачи рассматривается как постоянная; х- переменную, область изменения которой есть множество чисел, например действительных (обычно в задаче это как-то оговаривается). Кроме того, полезно вспомнить, что означает уравнение. Тогда условия этой задачи таковы:
1) а- есть параметр;
2) х- переменная, область изменения которой есть множество действительных чисел;
3) ax2- x3 + a2x - a =0 есть высказывание с переменной х.
Требование этой задачи тогда можно так сформулировать: найти все такие значения переменной х из области ее изменения, при которых указанное высказывание становится истинным.
Анализ задачи можно продолжить еще дальше. Можно спросить: что значит найти значения переменной х при данных условиях? Найдя ответ на этот вопрос, тем самым уточним требование задачи. Оно примет такой вид: найти такие выражения х от а, которые, будучи подставлены в заданное высказывание с переменной вместо х, обращают его в истинное высказывание при всех допустимых значениях параметра а.
Как видим, анализ задачи и вычленение ее условий, и требований можно производить с разной глубиной. Глубина анализа зависит главным образом от того, знакомы ли мы с видом задач, к которому принадлежит заданная, и знакомы ли с общим способом решения этих задач. Если да, то нам достаточен простейший анализ, сводящийся к установлению вида данной задачи; если нет, то для нахождения решения задачи нужен более глубокий анализ.
Для некоторых более сложных задач рассмотренный выше анализ (расчленение задачи на отдельные условия и требования) целесообразно продолжить. А именно установить, как устроены (из чего состоят) вычлененные условия.
3адача 4. К двум окружностям, радиусы которых 4 см и 6 см, проведены внутренние общие касательные оказавшиеся взаимно перпендикулярными. Вычислить расстояние между центрами окружностей.
Эта задача содержит такие условия:
1) дана окружность с центром О1 , радиус которой равен 4 см (здесь слово <дано> означает, что эта окружность построена из произвольного центра О1 );
2) из некоторого другого центра О2 проведена окружность радиуса 6 см;
3) эти две окружности построены так, что к ним можно провести общие внутренние касательные;
4) общие внутренние касательные к этим двум окружностям взаимно перпендикулярны.
Анализируя эти условия, можно заметить, что каждое из них состоит из одного или нескольких объектов и некоторой их характеристики. Так, объектом первого условия является окружность, а ее характеристикой; радиус этой окружности равен 4 см. Во втором условии объектом является также окружность с характеристикой: ее радиус равен 6 см. В третьем условии два объекта: указанные выше две окружности, а характеристикой является их взаимное расположение на плоскости: они расположены так, что к ним можно провести внутренние общие касательные. Наконец, четвертое условие содержит два объекта: общие внутренние касательные к окружностям, в качестве характеристики указано их отношение: они взаимно перпендикулярны.
Итак, мы видим, что в каждом условии задачи имеется один или два (в некоторых случаях больше) объекта; если в условии один объект, то указывается его характеристика в виде некоторого свойства этого объекта; если же объектов два, то характеристикой служит некоторое отношение этих объектов.
Довольно часто анализ задачи (ее расчленение на условия и требования, выделение в условиях объектов и их характеристик) сопряжен с большими трудностями. Приведем пример.
3адача 5. Две окружности взаимно касаются в точке X и касаются одной и той же прямой соответственно в точках A и B. Какую фигуру образует множество всех точек X, если радиусы данных окружностей будут принимать всевозможные значения?
На первый взгляд кажется, что в задаче речь идет о двух окружностях. Но прочтите еще раз внимательно вопрос задачи: требуется установить, какую фигуру образуют точки X (точка X- переменная). Значит, речь идет о множествах окружностей и множестве точек их касания. Исходя из этого, задачу можно расчленить на такие условия:
1. Дано множество окружностей, каждая из которых касается данной прямой в данной на ней точке A.
Здесь объектом является множество окружностей, а их характеристикой - свойство каждой окружности этого множества: она касается данной прямой в точке A.
2. Дано множество окружностей, каждая из которых касается данной прямой (с той же стороны, что и первое множество окружностей) в данной точке B.
Объект и характеристика этого условия аналогичны первому условию.
3. Из этих двух множеств образованы такие пары окружностей, причем, первый элемент пары есть окружность первого множества, а второй элемент пары - окружность второго множества, которые взаимно касаются.
Объектом этого условия является множество пар окружностей, а их характеристикой - отношение: окружности, входящие в пару, взаимно касаются.
Заметим, что в это множество пар окружностей войдут не все окружности первого и второго множеств окружностей, а лишь те из них, которые удовлетворяют указанному отношению (взаимное касание).
4. X- есть точка, в которой взаимно касаются соответствующие окружности, входящие в образованные пары (по третьему условию). Объектом этого условия является точка X (переменная точка), а ее характеристикой - свойство: эта точка есть точка касания окружностей, входящих в пару.
5. Множество точек X есть некоторая геометрическая фигура. Объектом условия является множество точек X взаимного касания окружностей, входящих в пары, а характеристикой - искомое свойство этого множества как геометрической фигуры.
Требование задачи состоит как раз в том, чтобы найти эту последнюю характеристику объекта пятого условия.
Некоторые из вас могут усомниться: нужен ли такой анализ для решения задачи? Ведь обычно, решая задачи, мы, мол, не производим такой анализ. Но это вам только кажется, что вы, решая задачи, не производите такого анализа. Вы просто не замечаете этого, ибо обычно такой анализ производится устно по ходу решения и притом этот анализ мы большей частью не осознаем. Но мы его производим, ибо без него решить задачу невозможно!
Результаты предварительного анализа задач надо как-то зафиксировать, записать. Та словесная, описательная форма записи, которую мы использовали выше, конечно, мало удобна. Надо найти более удобную, более компактную и в то же время достаточно наглядную форму записи результатов анализа задач. Такой формой является схематическая запись задачи.
Заметим, что не для всякой задачи надо делать схематическую запись. Так, например, для задач по решению уравнений, неравенств, преобразований выражений анализ проводится обычно устно и никак не оформляется. Вообще для задач, которые записаны на символическом языке (с помощью общепринятых обозначений и символов) схематическая запись не нужна.
Первой отличительной особенностью схематической записи задач является широкое использование в ней разного рода обозначений, символов, букв, рисунков, чертежей и т.д. Второй особенностью является то, что в ней четко выделены все условия и требования задачи, а в записи каждого условия указаны объекты и их характеристики, наконец, в схематической записи фиксируется лишь только то, что необходимо для решения задачи; все другие подробности, имеющиеся в задаче, при схематической записи отбрасываются.
На практике используется много разных видов схематической записи задач. Покажем на примерах.
3адача 6. С одного участка собрали 1440 ц пшеницы, а с другого, площадь которого на 12 га меньше, - 1080 ц. Найти площадь первого участка, если известно, что на первом участке собирали пшеницы с каждого гектара на 2 ц больше, чем на втором.
Анализ задачи показывает, что в ней рассматривается сбор урожая пшеницы с двух участков, при этом этот сбор характеризуется тремя величинами: массой собранной пшеницы, площадью участка и урожаем с одного гектара. Исходя из этого, составим таблицу для схематической записи условий и требований задачи, в которой две строки (первый и второй участки) и три столбца (общая масса собранной пшеницы, урожай с 1 га, площадь участка). Неизвестные величины, встречающиеся в задаче, запишем в таблице буквами, притом искомое обозначим буквой ![]() :
:
Участки |
Масса собранной пшеницы в ц |
Урожай с 1 га в ц |
Площадь участка в га |
Первый |
1440 |
а+2 |
х |
Второй |
1080 |
а |
х-12 |
В этой схематической записи выделены все условия, их объекты и характеристики. Указано и требование задачи: найти (искомую площадь первого участка). В то же время эта запись очень компактная, наглядная и полностью заменяет саму формулировку задачи.
3адача 7. Составить уравнение, корни которого были бы соответственно равны квадратам корней уравнения 2х2- 5x +1 = 0
Вычленим сначала требование задачи: составить уравнение. Какое уравнение нужно составить? В задаче сказано, что нужно составить уравнение, корни которого равны соответственно квадратам корней заданного уравнения, а последнее есть квадратное. Оно имеет два корня (каких - это в данном случае несущественно). Поэтому и искомое уравнение должно иметь два корня. Простейшее уравнение, имеющее два корня,- это квадратное. Следовательно, можно считать, что искомое уравнение - это квадратное.
А что значит составить квадратное уравнение? Очевидно, что это значит найти его коэффициенты. Обозначим их буквами a, b и c, а переменную искомого уравнения буквой y; с тем чтобы отличить это уравнение от данного.
Теперь мы можем сделать схематическую запись задачи в таком виде:
Дано:
1) корни уравнения 2х2- 5x +1 = 0 есть x1 и x2,
2) корни уравнения ay2- by +c = 0 есть y1 и y2,
3) y1= x12;
4). y2= x22
Найти: a, b, c.
Задачи, которые вы решаете в школе, различаются в первую очередь характером своих объектов. В одних задачах объектами являются реальные предметы, в других - все объекты математические (числа, геометрические фигуры, функции и т.д.). Первые задачи, в которых хотя бы один объект есть реальный предмет. Называются практическими (житейскими, текстовыми, сюжетными); вторые, все объекты которых математические, называются .математическими задачами.
Приведем пример практической задачи.
3адача 8. Телефонная проволока длиной 15 м протянута от столба, где она прикреплена на высоте 8 м от поверхности земли, к дому, где ее прикрепили на высоте 20 м. Найдите расстояние между домом и столбом, предполагая, что проволока не провисает.
Объектами этой задачи являются вполне реальные предметы: проволока, столб, дом. Поэтому это практическая задача. Чтобы ее решить с помощью математики, надо построить соответствующую ей математическую задачу, которая получается путем отвлечения от конкретных особенностей реальных предметов и заменой их математическими объектами. В данном случае проволоку, столб и дом (точнее, стену дома) можно рассматривать как отрезки. Считая, что поверхность земли есть прямая, а отрезки, изображающие столб и дом, перпендикулярны к этой прямой, получаем такую математическую задачу.
3адача 9. Отрезки длиной 8 м и 20 м перпендикулярны к прямой, соединяющей их концы и расположены по одну сторону от этой прямой. Отрезок, соединяющий другие концы этих отрезков, имеет длину 15 м. Найти расстояние между первыми двумя отрезками.
Заметим, что в курсе математики решаются лишь такие практические задачи, которые сводимы к математическим. Решение же математических задач и сводимых к ним практических рассмотрим ниже.
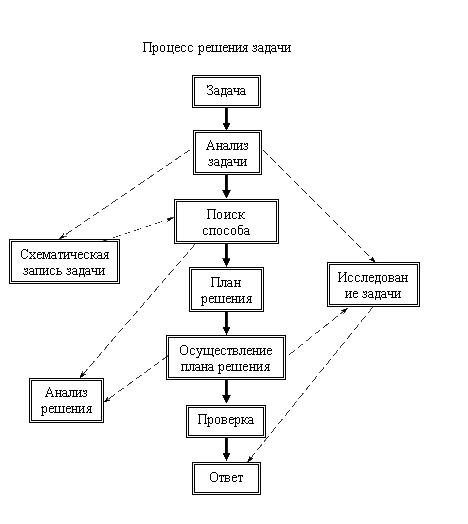
Когда в предыдущем разделе мы выписывали решения задач, то эти записи представляли собой лишь изложения самого решения. Но как эти решения были найдены, как убедились, что они правильные, - обо всем этом ничего не было сказано. Если под процессом решения задач понимать процесс, начинающийся с момента получения задачи до момента полного завершения ее решения, то, очевидно, что этот процесс состоит не только из изложения уже найденного решения, а из ряда этапов, одним из которых и является изложение решения.
Из каких же этапов состоит процесс решения задачи? Очевидно, что, получив задачу, первое, что нужно сделать, это разобраться в том, что это за задача, каковы ее условия, в чем состоят ее требования, т. е. провести тот анализ задачи, о котором говорилось в первой главе. Этот анализ и составляет первый этап процесса решения задачи.
В ряде случаев этот анализ надо как-то оформить, записать. Для этого, как вы знаете, используются разного рода схематические записи задач, построение которых составляет второй этап процесса решения.
Анализ задачи и построение ее схематической записи необходимо главным образом для того, чтобы найти способ решения данной задачи. Поиск этого способа составляет третий этап процесса решения.
Когда способ решения задачи найден, его нужно осуществить, - это будет уже четвертый этап процесса решения - этап осуществления (изложения) решения.
После того как решение осуществлено и изложено (письменно или устно), необходимо убедиться, что это решение правильное, что оно удовлетворяет всем требованиям задачи. Для этого производят проверку решения, что составляет пятый этап процесса решения.
При решении многих задач, кроме проверки, необходимо еще произвести исследование задачи, а именно установить, при каких условиях задача имеет решение и при том сколько различных решений в каждом отдельном случае; при каких условиях задача вообще не имеет решения и т.д. Все это составляет шестой этап процесса решения.
Убедившись в правильности решения и, если нужно, произведя исследование задачи, необходимо четко сформулировать ответ задачи,- это будет седьмой этап процесса решения.
Наконец, в учебных и познавательных целях полезно также произвести анализ выполненного решения, в частности установить, нет ли другого, более рационального способа решения, нельзя ли задачу обобщить, какие выводы можно сделать из этого решения и т.д. Все это составляет последний, конечно не обязательный, восьмой этап решения.
Итак, весь процесс решения задачи можно разделить на восемь этапов:
l-й этап - анализ задачи;
2-й этап - схематическая запись задачи;
3-й этап - поиск способа решения задачи;
4-й этап - осуществление решения задачи;
5-й этап - проверка решения задачи;
6-й этап - исследование задачи;
7-й этап - формулирование ответа задачи;
8-й этап - анализ решения задачи.
Приведенная выше схема процесса решения задач является лишь примерной. При фактическом решении указанные там этапы обычно не отделены друг от друга, а переплетаются между собой. Так в процессе анализа задачи обычно производится и поиск решения. При этом полный план решения устанавливается не до осуществления решения, а в его процессе. Тогда поиск решения ограничивается лишь нахождением идеи решения. Порядок этапов также иногда может меняться.
Из указанных восьми этапов пять являются обязательными, и они имеются (в том или ином виде) в процессе решения любой задачи. Это этапы анализа задачи, поиска способа ее решения, осуществления решения, проверки решения и формулирования ответа. Остальные три этапа (схематическая запись задачи, исследование задачи и заключительный анализ решения) являются не обязательными и в процессе решения многих задач не имеются.
Анализ задачи, т.е., выяснение характера задачи, ее вида, установление ее условий и требований (конечно не всегда в полном объеме), мы производим в процессе решения любой, даже самой простейшей задачи. Когда мы читаем, например, такую задачу: Решить уравнение 2х2- 5x +1 = 0 - и говорим: <Это квадратное уравнение>, то уже тем самым мы произвели анализ этой задачи. Конечно, это самый простейший анализ, состоящий в установлении вида задачи, но в данном случае он вполне достаточен. Для других, более сложных задач понадобится и более развернутый, более многоплановый и сложный анализ. Заметим, что при решении особо сложных задач анализ приходится производить не один раз, при первичном чтении задачи, а многократно, при каждой новой попытке решения (а их может быть несколько), в процессе самого решения, при переходе к каждому очередному шагу решения.
Точно так же поиск способа решения производится в процессе решения любой задачи. Даже в указанной выше задаче, после того как установили, что это есть квадратное уравнение, обычно говорим (вслух или мысленно): Для его решения используем формулу корней приведенного квадратного уравнения>. Этим самым мы и произвели поиск способа решения. При решении более сложных задач поиск способа решения является самым трудным и основным этапом решения. Он может занимать и по времени самое большое место в общем процессе решения. При этом довольно часто поиск способа решения приходится производить не один раз. Когда в процессе выполнения найденного способа решения мы убеждаемся в его ошибочности или сложности, то приходится снова возвращаться к этапу поиска решения и искать другой способ решения. И так зачастую приходится делать много раз. Тут нужно, конечно, упорство, но еще важней каждый раз в случае неудачи поиска решения возвращаться к анализу задачи, производить его еще раз более внимательно и искать причины этих неудач.
Что касается этапа осуществления решения, то очевидно, что без него и нет самого решения.
Сложнее с этапом проверки решения. Большей частью проверка решения производится попутно по мере осуществления решения, и, как правило, она производится устно. В этом случае эта проверка является формой самоконтроля за своими действиями. При этом часто мы даже не осознаем, что производим проверку самоконтроль. Но это тогда, когда имеется прочная привычка к такому самоконтролю и хороший навык к тому. Тем же из вас, кто такой привычкой и навыком не обладает, советуем производить проверку каждый раз, с тем чтобы в конечном итоге приобрести такой навык.
Формулирование ответа не всегда выделяется в особый этап, но, если ответ особо не выписывается, надо все же его как-то выделить (например, путем подчеркивания).
Хотя этап схематической записи является и не обязательным, но мы советуем им не пренебрегать. Схематическая запись служит очень хорошей формой, организующей и глубокий и планомерный анализ задачи, и поэтому этот этап всегда сливается с анализом задачи. Схематическая запись, кроме того, облегчает само решение, ибо, опираясь, на эту запись, легче и проще оформить решение.
Что касается анализа решения, то следует учесть, что решение школьных задач является не самоцелью, а средством обучения. Поэтому обсуждение проделанного решения, выявление его недостатков, поиск других способов, установление и закрепление в памяти тех приемов, которые были использованы в данном решении, выявление условий возможности применения этих приемов - все это как раз и будет способствовать превращению решения задач в могучее обучающее средство.
При анализе решения полезно устанавливать возможность обобщения данной задачи, выявлять ее особенности, сопоставлять решение данной задачи с ранее решенными и т.д.
Если вы хотите по-настоящему научиться решать задачи, то анализируйте решение каждой мало-мальски новой и более или менее сложной задачи. Не жалейте на это времени и сил: все это в будущем окупится.
В заключение обращаем ваше внимание на некоторую особенность использования термина <решение задачи>. Дело в том, что этим термином обозначаются два связанных между собой, но все же неодинаковых понятия. Когда мы говорим: <процесс решения задачи>, то здесь под решением задачи понимается вся деятельность человека, решающего задачу, с момента начала чтения задачи до конца. Когда же мы говорим: <поиск решения задачи> или <анализ решения задачи>, <осуществление решения задачи>, то здесь под решением задачи понимаются лишь те действия, которые мы производим над условиями и их следствиями на основе общих положений математики для получения ответа задачи. Было бы, пожалуй, целесообразно как-то различать эти два аспекта понятия <решение задачи> (например, второй называть <непосредственное решение задачи>), но обычно это не делают, а из самого контекста ясно, о каком аспекте идет речь . Это следует вам иметь в виду при чтении данной книги.
Заметим, что иногда термин <решение задачи> используется ещё и в третьем аспекте, а именно в смысле результата (ответа) задачи. Например, когда говорят: <решением системы уравнений называется и т.д.> или <мы нашли два решения этой задачи>, то как раз имеют в виду этот аспект термина <решение задачи>.
В определении стандартных задач в качестве основного признака этих задач указано наличие в курсе математики таких общих правил или положений, которые однозначно определяют программу решения этих задач и выполнение каждого шага этой программы.
Отсюда понятно, что нестандартные задачи - это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения.
Рассмотрим примеры решения таких задач, с тем чтобы выяснить особенности процесса их решения.
3адача 10. Расстояние от реки до турбазы туристы рассчитывали пройти за 6 ч. Однако после 2 ч пути они уменьшили скорость на 0,5 км/ч и в результате опоздали на турбазу на 30 мин. С какой скоростью шли туристы первоначально?
Решение. Эта задача является практической (текстовой). Для подобных задач никакого общего правила определяющего точную программу их решения, не существует. Однако это не значит, что вообще нет каких-то общих указаний для решения таких задач. Подробно сущность этих указаний мы рассмотрим в следующей главе. А пока лишь покажем, как эти указания практически используются.
Обозначим искомую первоначальную скорость туристов через х км/ч. Тогда за 6 ч, за которые они рассчитывали пройти расстояние от реки до турбазы, они прошли 6 х км. Фактически этот путь они прошли следующим образом: 2 ч они шли с первоначальной скоростью, а затем еще 4,5 ч (ибо они опоздали на 0,5 ч к сроку) - с уменьшенной скоростью (x - 0,5) км/ч. Следовательно, они прошли 2х км и 4,5(x -0,5) км, а всего 2х +4,5(x-0,5)км, что равно расстоянию от реки до турбазы, т.е. 6 х км. Получаем уравнение: 2х + 4,5(x -0,5) = 6x.
Решив это уравнение, найдем: x = 4,5.
Значит, первоначальная скорость туристов равна 4,5 км/ч. Проанализируем процесс приведенного решения задачи 25. Сначала мы определили вид задачи , и, исходя из этого, возникла идея решения . Для этого, пользуясь весьма общими указаниями и образцами решения подобных задач, полученных в школьном курсе математики (надо обозначить одно из неизвестных буквой, например х , и выразить остальные неизвестные через х , затем составить равенство из полученных выражений), мы построили уравнение. Заметим, что эти указания, которыми мы пользовались, не являются правилами, ибо в них ничего не сказано, какое из неизвестных обозначить через х , как выразить остальные неизвестные через х , как получить нужное равенство и т.д. Все это делается каждый раз по-своему, исходя из условий задачи и приобретенного опыта решения подобных задач.
Полученное уравнение представляет собой уже стандартную задачу. Решив ее, мы тем самым решили и исходную нестандартную задачу.
Таким образом, смысл процесса решения данной задачи состоит в том, что с помощью особого приема (составления уравнения) мы свели ее решение к решению эквивалентной стандартной задачи.
Когда приступаем к решению какой-либо задачи, то первое, что хочется, естественно, узнать, - это: что это за задача? Какого она вида, типа? Иными словами, нужно распознать вид данной задачи.
Если мы сумеем это сделать, установим, к какому виду задач она принадлежит, то тем самым сделаем первый, очень важный шаг в поисках плана ее решения. Ведь, зная вид задачи, в большинстве случаев получаем и способ ее решения, ибо в курсе математики для многих видов задач имеются общие правила их решения.
Как же распознать вид задачи?
Для этого, очевидно, нужно знать основные виды математических задач и их признаки.
Первым признаком, по которому все математические задачи делятся на отдельные виды или классы, является характер требования задачи. По этому признаку все задачи делятся на три основных класса.
1-й класс. Задачи на нахождение искомого
В задачах этого класса требование состоит в том, чтобы найти, разыскать, распознать какое-то и искомое. При этом искомым могут быть величина, отношение, какой-либо объект, предмет, его положение или форма и т.д.
Очевидными примерами задач этого класса являются задачи на вычисление различных выражений, значений функций, задачи на установление характера функции и т.д.
К ним же относятся геометрические вычислительные задачи, где нужно найти длину отрезка, величину угла, площадь фигуры, объем тела и т.п.
Многочисленные задачи на решение различных уравнений, систем уравнений, неравенств и их систем также принадлежат к этому классу задач, ибо в каждой из них нужно найти значения некоторых переменных, удовлетворяющих определенным условиям.
Задачи, в которых нужно установить вид заданных выражений, чисел, форму заданной геометрической фигуры или тела, -это опять-таки задачи рассматриваемого класса.
Как видим, этот класс задач чрезвычайно многочисленный и разнообразный. Поэтому, естественно, для решения задач этого класса нет какого-либо общего метода. Но все же знание, что данная задача принадлежит к рассматриваемому классу, сужает область поисков плана решения и служит ориентиром в этих поисках. Можно даже высказать такую весьма общую рекомендацию: если вы установили, что данная задача есть задача нахождения искомого, и вы не смогли найти более простого решения, то сведение данной задачи к какому-либо известному виду уравнений, неравенств или систем всегда приведет к решению этой задачи.
2-й класс. Задачи на доказательство или объяснение
В задачах этого класса требование состоит в том, чтобы убедиться в справедливости некоторого утверждения, или проверить верность или ложность этого утверждения, или, наконец, объяснить, почему имеет место то или иное явление, тот или иной факт.
Все задачи, требование которых начинается со слов "<доказать> почему?" или содержащие вопрос , обычно относятся к этому классу задач.
3-й класс. Задачи на преобразование или построение
К этому классу относятся задачи, в которых требуется преобразовать какое-либо выражение, упростить его, представить в другом биде, построить что-либо (например, геометрическую фигуру или выражение), удовлетворяющее указанным условиям.
Класс этих задач также весьма многочисленный и разнообразный. Характерной особенностью задач этого класса является то, что в каждой из них заданы какие-то объекты (элементы, выражения), из которых требуется создать, построить, сконструировать другой какой-то объект с заранее известными свойствами.
Например, задано выражение и из него нужно получить (построить) другое выражение, обладающее какими-то особенностями (скажем, тождественно равное данному, но записанное в стандартном виде и т.д.). Или заданы элементы геометрических фигур и из них (с помощью определенных инструментов) нужно построить сами эти фигуры и пр.
Для того чтобы установить вид задачи, особое внимание следует уделить анализу требования (вопроса) задачи. Иногда в самом требовании указан вид задачи, например: решите квадратное уравнение 2х2- 5x +1 = 0>. Но большей частью вид задачи в требовании прямо не указан и лишь анализ этого требования может помочь определить вид задачи.
Так, в задаче: <найти точки пересечения графика функции y= 2х2- 5x с осью абсцисс> - требование не содержит прямого указания на вид этой задачи. Но если мы внимательно проанализируем это требование (найти точки пересечения графика функции, т.е. кривой, с осью абсцисс), то легко поймем, что имеем дело с той же задачей решения квадратного уравнения.
Конечно, в ряде случаев распознавание вида задачи представляет собой довольно сложное дело. Приведем пример.
3адача 11. Сколько центров гомотетии имеют два равных круга?
На первый взгляд кажется, что эта задача какого-то вида на нахождение искомого. К такому выводу нас наталкивает вопрос: "сколько?" значит, надо что-то найти. Но не следует спешить, вдумаемся в требование задачи. Нужно найти число центров гомотетии двух равных кругов. Следовательно, эти два равных круга даны и их надо рассматривать как гомотетичные фигуры, а требуется найти центры гомотетии, только тогда мы сможем пересчитать их и установить, сколько их. А что значит найти центры гoмотетии? Это значит по данным гомотетичным фигурам построить их центр гомотетии. Значит, данная задача фактически является задачей на построение, притом весьма своеобразной, ибо по заданным геометрическим фигурам, которые гомотетичны, необходимо построить (восстановить) их центр гомотетии. Подсчет же числа этих центров (после их построения) уже задачи не представляет.
Итак, анализ требования задачи для распознавания ее вида связан с переформулированием этого требования, с заменой его другим, знакомым, но, конечно, эквивалентным первоначальному.
Что дает нам распознавание вида задачи?
Очень многое. Ведь для большинства видов в школьном курсе математики вы изучали методы решения этих задач, и, следовательно, установив принадлежность данной задачи к определенному виду, тем самым получаем готовый план ее решения: применить известный метод решения подобных задач.
Конечно, вам встретятся задачи, определить вид которых вы не сумеете или это будет такой вид, для которого вам неизвестен общий метод решения. Что ж, тогда надо будет использовать другие приемы (например, разбиение на подзадачи известного вида и др.)
Известный советский математик, профессор московского университета Софья Александровна Яновская (1896-1966) однажды выступила перед участниками математических олимпиад с лекцией <что значит решить задачу?>. Ее ответ оказался поразительно простым, но несколько неожиданным для слушателей: <решить задачу - значит свести ее к уже решенным>.
Для вас этот ответ С.А. Яновской не должен быть неожиданным. Ведь в предыдущей главе мы уже говорили, что решение нестандартных задач, а именно их, конечно, имела в виду С.А. Яновская, состоит в сведении их путем преобразования или переформулирования к стандартным задачам или же в разбиении их на стандартные подзадачи, что также означает сведение к стандартным задачам. А что значит свести решение нестандартной задачи к решению стандартных задач? Это и означает, что мы сводим решение данной (незнакомой) задачи к ранее решенным задачам, ибо стандартные задачи можно рассматривать как такие, которые каждый из вас уже умеет решать и не однажды решал.
Когда мы приступаем к решению какой-либо задачи и в результате ее анализа не сумеем распознать в ней знакомый вид, иными словами, обнаружим, что данная задача принадлежит к незнакомому нам виду, для которого нам неизвестен общий метод решения, то что нам остается делать? Только попытаться свести к знакомым, ранее решенным задачам (с помощью преобразования, переформулирования и др.). Это-то и рекомендовала делать С.А. Яновская.
Психология уже свыше ста лет занимается исследованием процессов решения задач человеком. В результате этих исследований открыто много интересных закономерностей и найдены важные характеристики процессов решения задач. Особый интерес представляет общая характеристика этого процесса, данная известным советским психологом Сергеем Леонидовичем Рубинштейном (1889-1960) .Он характеризовал решение задач человеком как процесс их переформулирования, в котором непрерывно производится анализ условий и требований задачи через синтетический акт их соотнесения.
Действительно, выше вы неоднократно наблюдали это переформулирование задач, их преобразование в процессе анализа и поисков решения. Мы уже не раз отмечали эту характерную особенность процессов решения, однако, пожалуй, стоит ее рассмотреть более подробно. Ведь одного указания на эту особенность процесса решения задач, указания на анализ и синтез как средства переформулирования и решения недостаточно для того, чтобы сознательно использовать их для решения задач. Естественно возникают вопросы: а в чем состоит это переформулирование? Что мы делаем с задачей, когда ее переформулируем? Что получаем? Какими средствами производится переформулирование?
Чтобы разобраться во всех этих вопросах, рассмотрим пример переформулирования задач в процессе анализа и решения.
Задача 12. Некоторая коллекция значков была размещена в коробках, каждая из которых имела 10 отделений. В некоторые отделения коробок были положены значки, по одному в отделение, другие отделения были еще пустые. Любые две коробки этой коллекции отличались друг от друга хотя бы наличием или отсутствием значков в одном и том же отделении. Очевидно, что наибольшее число значков в коробке равно 10, а наименьшее - нуль (коробка пустая). Сколько коробок в этой коллекции?
Эта задача, конечно, носит несколько необычный характер. Но вот подобная ей задача, имеющая уже более реальный характер, полученная из задачи 23 с помощью такого переформулирования: каждому отделению коробки поставим в соответствие электрическую лампочку, тогда наличию или отсутствию в нем значка соответствует одно из возможных состояний лампочки (горит или не горит). В результате получаем такую задачу.
3адача 13. В квартире 10 лампочек. Сколько существует различных способов освещения квартиры? Два способа освещения считаются различными, если они отличаются состоянием хотя бы одной лампочки. Каждая лампочка может гореть и не гореть. Случай, когда все лампочки не горят - это тоже способ освещения.
Хотя эта задача более реальная и явление, в ней описанное, более наглядное, но и ее решение не очевидно.
Чтобы легче подсчитать все различные способы освещения квартиры (или число коробок), изобразим каждую лампочку (каждое отделение) в виде квадрата, а ее состояние будем отмечать знаком <+>, если лампочка горит (значок имеется), и знаком <-> в противном случае. Тогда каждому способу освещения квартиры (каждой коробке) будет соответствовать строка из десяти квадратиков со знаком <+> или <->. Число же таких строк в таблице и есть искомое число различных способов освещения квартиры (число коробок).
Получаем такую задачу.
3адача 14. Имеется прямоугольная таблица, содержащая 01 столбцов. В каждой клеточке этой таблицы поставлен знак <+> или <->. Любые две строки таблицы отличаются знаком в клеточках, стоящих хотя бы в одном и том же столбце. Какое наибольшее число строк имеет эта таблица?
Если решение и этой задачи вам не очевидно, то можно построить еще более прозрачную задачу следующим образом. Будем рассматривать каждую строку таблицы, о которой идет речь в предыдущей задаче, как десятизначное число, составленное из цифр 1 и 0 (цифра 1 соответствует, знаку <+> в клеточке, а цифра 0 - знаку <->). Тогда задача 14 переформулируется в такую.
3адача 15. Сколько различных десятизначных чисел можно образовать из цифр 0 и 1? При этом числа, в записи которых стоят слева одни нули (например, 0100001101, или 000000001, или даже 0000000000), также рассматриваются.
Решение этой последней задачи уже очевидно. На каждом месте в записи десятизначного числа могут стоять лишь цифры 1 или 0. Поэтому имеется всего лишь две комбинации цифр на каждом месте. Эти комбинации независимы друг от друга, ибо проставление цифры на данном месте в записи числа не зависит от того, какие цифры стоят на других местах. Поэтому общее число комбинаций или возможных десятизначных различных чисел равно 210.
Итак, общее число коробок из задачи 12, число способов освещения квартиры из задачи 13, число строк в таблице из задачи 14 и число десятизначных чисел из задачи 15 равно 1024.
Задачи 13-15 были получены из задачи 12 с помощью ее переформулирования. Чем же они являются для нее?
Оказывается, что все они являются ее моделями, следовательно, переформулирование задачи 12 явилось способом ее моделирования, построения ее моделей.
Что такое модель и моделирование?
В науке широко используется метод моделирования. Заключается он в том, что для исследования какого-либо явления или объекта выбирают или строят другой объект, в каком-то отношении подобный исследуемому. Построенный или выбранный объект изучают и с его помощью решают исследовательские задачи, а затем результаты решения этих задач переносят на первоначальное явление или объект.
Пример. Люди издавна интересуются, как устроена наша Вселенная. Этот интерес не только чисто познавательный, но и сугубо практический, ибо люди хотели научиться предсказывать периодические явления, связанные с устройством Вселенной, такие, как затмения Солнца и Луны, наступление времен года и т.д. Для решения этих задач ученые строили свои представления о Вселенной в виде схемы - картины мира, в которой объекты Вселенной - Солнце и звезды, планеты, Земля и Луна изображались точками, движущимися по каким-то кривым - траекториям их движения. Таковы, например, схемы, построенные Птолемеем, в которых центральное место занимала наша Земля, или схема Коперника, в которой центр занимало Солнце. С помощью этих схем ученые решали задачи предсказания отдельных астрономических явлений.
Эти схемы, эти картины мира суть модели Вселенной, а метод исследования Вселенной, нахождения законов о Вселенной и решения задач, связанных с нею, с помощью этих моделей является методом моделирования.
Другой пример. Люди издавна интересуются, как они сами устроены, как функционирует человеческий организм. Но исследовать эти вопросы на живом человеческом организме очень трудно, ибо такое изучение до появления особых при боров было связано с гибелью этого организма. Тогда ученые стали исследовать устройство человеческого организма на подобных ему организмах животных (обезьян, собак и пр.). Изучение организма животных, их функционирования помогло установить многие важнейшие закономерности функционирования человеческого организма. Вспомните, к примеру, знаменитые исследования П. Павлова на собаках. В этих исследованиях животные организмы выступали в качестве моделей человеческого организма, а применяемый при этом метод исследования есть метод моделирования.
Еще пример. Разрезая конус плоскостями, получаем в сечении различные кривые: окружности, эллипсы, параболы, гиперболы. Математики еще в древности начали изучение этих кривых, результаты которых имеют большое значение для физики, астрономии, техники, военного дела, где очень часто встречаются эти кривые. Однако лишь тогда, когда, пользуясь методом Декapтa и Ферма, были составлены уравнения этих, кривых, их изучение сразу резко подвинулось вперед и с помощью этих уравнений - моделей кривых конических сечений - были решены все основные задачи, с ними связанные. Заметим, что уравнения выступают в качестве моделей окружности, эллипса, параболы и гиперболы, а эти кривые в свою очередь можно рассматривать как геометрические модели указанных уравнений.
Теперь должно быть вам ясно, что рассмотренные выше задачи 13-15 являются моделями задачи 12, а переформулирование задачи 12 последовательно в задачи 13-15 является способом построения моделей этой задачи, т.е. способом ее моделирования. Можно сказать, что мы осуществили решение задачи 12 методом ее моделирования.
Вспоминая, как мы решали задачи, как искали их решения; можно установить, что в процессах решения многих задач мы широко использовали моделирование этих задач.
В заключении сформулируем основные рекомендации для поиска решения математических задач.
1. Прочтя задачу, надо попытаться установить, к какому виду задач она принадлежит.
2. Если вы узнали в ней стандартную задачу знакомого вида, то примените для ее решения известное вам общее правило.
3. Если же задача не является стандартной, то следует действовать в следующих направлениях:
а) вычленять из задачи или разбивать ее на подзадачи стандартного вида (способ разбиения);
б) ввести в условие вспомогательные элементы: вспомогательные параметры, вспомогательные построения (способ вспомогательных элементов);
в) переформулировать ее, заменить ее другой равносильной задачей (способ моделирования).
4. Для того чтобы легче было осуществлять указанные способы, полезно предварительно построить наглядную вспомогательную модель задачи - ее схематическую запись.
5. Решение нестандартных задач есть искусство, которым можно овладеть лишь в результате глубокого постоянного самоанализа действий по решению задач и постоянной тренировки в решении разнообразных задач.
Помните, что решение задач есть вид творческой деятельности, а поиск решения есть процесс изобретательства.