2.1. Классическое определение вероятности
Любое наблюдение или эксперимент в теории вероятностей называется испытанием, а результат испытания - событием. Событие называется
случайным, если в данном испытании оно может произойти, а может не произойти.
Если в данном испытании событие обязательно происходит, оно называется достоверным, а если заведомо не может произойти -
невозможным.
Например, рассмотрим испытание, которое заключается в одном бросании игральной кости. (Игральная кость - это кубик, на шести гранях которого нанесены числа от 1 до 6). Выпадение любого
числа очков от 1 до 6 - это случайное событие, выпадение менее 8 очков - достоверное событие, более 6 очков - невозможное.
События будем обозначать большими буквами латинского алфавита A, B, C, ...
Исходы испытания, результатом которых является некоторое событие А, назовем благоприятными исходами для этого события.
Так если событие А: "Выпадение четного числа очков на игральной кости", то исходы 2, 4, 6 будут благоприятными для события А.
Определение 2.1.
Вероятностью события А называется отношение
числа благоприятных исходов для события А к общему числу исходов.
Вероятность события А обозначается p(A).
 (2.1)
m - число благоприятных исходов; n - общее число исходов.
(2.1)
m - число благоприятных исходов; n - общее число исходов.
Это - классическое определение вероятности. Так, например,
вероятность выпадения герба при бросании монеты равна 1/2, а вероятность выпадения пяти очков при бросании игральной кости -1/6;
вероятность невозможного события равна 0, а достоверного - 1.
Из определения следует, что вероятность любого события есть
число, заключенное в промежутке [0; 1], то есть
 Определение 2.2.Два события А и В называются несовместимыми,
если появление одного из них исключает появление другого. В противном случае события называются совместимыми.
Определение 2.2.Два события А и В называются несовместимыми,
если появление одного из них исключает появление другого. В противном случае события называются совместимыми.
Так, например, при однократном бросании игральной кости события А: "Выпадение 5 очков" и В:"Выпадение 6 очков" - несовместимы, а событие С:
"Выпадение четного числа очков" совместимо с событием В.
Определение 2.3.
Два события называются противоположными
друг другу, если в данном испытании они несовместимы
и одно из них обязательно происходит.
Событие, противоположное А, обозначается  . Если общее число исходов некоторого испытания равно n и событию А благоприятствуют m исходов, то, очевидно, событию
. Если общее число исходов некоторого испытания равно n и событию А благоприятствуют m исходов, то, очевидно, событию
 благоприятствуют n -m исходов,
благоприятствуют n -m исходов,
 ,следовательно,
,следовательно,
 (2.2)
Сумма вероятностей противоположных событий равна 1. Так, если
вероятность попадания при выстреле в мишень равна 0,7, то вероятность
промаха будет 0,3.
(2.2)
Сумма вероятностей противоположных событий равна 1. Так, если
вероятность попадания при выстреле в мишень равна 0,7, то вероятность
промаха будет 0,3.
Определение 2.4.
Совокупность событий А1, А2, ... Аn образует полную группу событий для данного испытания, если
результатом испытания обязательно становится хотя бы одно из них.
Определение 2.5.
События А1, А2, ... Аn , образующие полную груп&пу попарно несовместимых и
равновозможных событий, называются элементарными событиями.
Именно такие события мы назвали исходами в определении вероятности.
2.2. Статистическое определение вероятности
Пусть А - случайное событие по отношению к некоторому испытанию. Проведем это
испытание n раз и пусть событие А произошло m раз.
Составим отношение
P·(A)= .
Оно называется относительной частотой события А. Эта частота
обладает свойством устойчивости: с увеличением количества опытов она приближается к некоторому постоянному числу,
стабилизируясь около него. Данный факт служит основой для еще одного определения вероятности - статистического.
.
Оно называется относительной частотой события А. Эта частота
обладает свойством устойчивости: с увеличением количества опытов она приближается к некоторому постоянному числу,
стабилизируясь около него. Данный факт служит основой для еще одного определения вероятности - статистического.
Определение 2.6.Вероятностью события А в данном
испытании называется число Р(А), около которого группируются значения относительной частоты при больших n.
Таким образом, относительная частота приближенно равна вероятности и тем точнее, чем больше число испытаний. Поэтому
на практике поступают следующим образом. Чтобы найти вероятность изготовления данным станком годной детали, проверяют некоторую
партию, например, из 200 деталей и определяют количество годных.
Допустим, их количество - 190. Относительная частота P·(A)= .Это число и принимают приближенно за вероятность нормальной работы станка.
.Это число и принимают приближенно за вероятность нормальной работы станка.
2.3. Геометрические вероятности
Рассмотрим такую задачу. Круглая мишень разбита на 4 сектора и вращается вокруг центра.
Стрелок стреляет в мишень один раз. Какова вероятность,что он попадет в сектор ОАВ ?Здесь классическое определение не годится, так как каждое событие изображается точкой круга,
а их - бесконечное множество. В этом случае вероятность попадания в сектор ОАВ будет равна отношению
площади сектора ОАВ к площади всего круга.
 .
Геометрическое определение вероятности события формулируется следующим образом.
.
Геометрическое определение вероятности события формулируется следующим образом.
Определение 2.7.
Вероятностью события называется отношение меры множества благоприятных
элементарных событий (исходов) к мере множества всех элементарных
событий.
В качестве меры, как правило, выступают длина, площадь и объем.
Рассмотрим примеры на вычисление вероятностей.
Пример 37.
На шести одинаковых карточках написаны буквы А, В, К ,С , О, М.
Карточки перемешиваются и раскладываются в ряд
случайным образом. Какова вероятность, что получилось слово "Москва"?
Решение.
Обозначим событие А: "Получилось слово "Москва"". По формуле (2.1)
 . Найдем n - общее число исходов. Если мы раскладываем 6 карточек
в ряд, то число всевозможных вариантов будет равно количеству
перестановок из шести элементов:
n = Р6 = 6! = 1·2·3·4·5·6=720.
А благоприятный исход всего один - когда получилось слово
"Москва". Итак, m = 1,
. Найдем n - общее число исходов. Если мы раскладываем 6 карточек
в ряд, то число всевозможных вариантов будет равно количеству
перестановок из шести элементов:
n = Р6 = 6! = 1·2·3·4·5·6=720.
А благоприятный исход всего один - когда получилось слово
"Москва". Итак, m = 1,
 .
.
Ответ: 1 / 720.
Пример 38.В урне 14
белых и 6 черных шаров. Из нее наугад извлекается один шар. Найти вероятность того, что этот шар - черный.
Решение.Пусть А:"Извлечен черный шар". Общее число исходов n = 20, благоприятных
m =6.
Ответ: 0,3
Пример 39.
Из букв слова "событие" наугад извлекаются и раскладываются в ряд 3
буквы. Какова вероятность, что получится слово "быт"?
Решение.
 , m =1,
, m =1,
 .
.
Ответ: 1 / 210.
Пример 40. Окрашенный
деревянный куб с ребром 10 см распилен на кубики с ребром 2 см.Кубики перемешали и наугад извлекли 1 кубик. Какова вероятность,
что он имеет
а) три окрашенные грани;
б) две окрашенные грани;
в)одну окрашенную грань;
г) не окрашен.
Решение.Каждое ребро
куба разбито на 5 частей, значит, всего кубиков 53 = 125.
Событие А: "У кубика 3 окрашенных грани". Такие кубики находятся в вершинах куба, их 8 штук, поэтому p(A)= 8/125.
В: "У кубика 2 окрашенных грани". Вдоль каждого ребра имеется
по 3 таких кубика, всего их - 3 ·12 = 36. P(B)= 36/125
С: "У кубика 1 окрашенная грань", m = 9 · 6 = 54, P(C)= 54/125.
D: "Кубик не окрашен". m = 27, P(D)= 27/125.
Заметим, что все эти вероятности в сумме дают 1 и образуют
полную группу событий.
Ответ:
Пример 41.В ящике
перемешаны 10 синих и 8 зеленых носков. Наугад вынимаются
2 носка. Какова вероятность, что они:
а)оба синие;
б)одного цвета;
в) разных цветов ?
Решение.
События, вероятность которых надо найти в пунктах а), б), в)
обозначим соответственно А, В, С. Поскольку во всех трех случаях из 18 носков выбирается 2, то общее число исходов
 Число благоприятных исходов в первом случае
Число благоприятных исходов в первом случае
 , во втором - по правилу суммы
, во втором - по правилу суммы  = 73,
в третьем - по правилу произведения m = 10 · 8 = 80.
Находим:
= 73,
в третьем - по правилу произведения m = 10 · 8 = 80.
Находим:  Ответ: 0,3; 0,48; 0,52
Ответ: 0,3; 0,48; 0,52
Пример 42. В коробке 5 красных и 7 зеленых карандашей. Из нее случайно
выпали 3 карандаша. Найти вероятность того, что два из них - красные?
Решение.А: "Выпало 2 красных и 1 зеленый карандаш". Общее число исходов
 Для нахождения m заметим, что 2 красных карандаша из 5 красных можно выбрать
Для нахождения m заметим, что 2 красных карандаша из 5 красных можно выбрать
 способами, а 1 зеленый из 7 зеленых -
способами, а 1 зеленый из 7 зеленых - способами.
И, по правилу произведения,
способами.
И, по правилу произведения, Итак,
Итак,
 Ответ: 0,32
Ответ: 0,32
Пример 43.По
многолетним наблюдениям среднее число солнечных дней в сентябре на Алтае равно 12. Какова вероятность, что 16
сентября будет пасмурная погода?
Решение.Здесь
мы используем статистическое определение и за вероятность приближенно принимаем относительную частоту пасмурных дней:
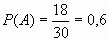
Ответ: 0,6.
Пример 44.В круг
радиуса 5 брошена точка. Найти вероятность того, что она окажется внутри вписанного в этот круг равностороннего
треугольника.
Решение.
Согласно геометрического определения, вероятность равна отношению площадей треугольника и круга. СО =5, СН = 1,5 · 5 = 7,5.
Полагая АН = х, АС =2х,по теореме Пифагора АС2 = АН2 + СН2,
4х2 = х2 + 7,52. Отсюда находим:
 ·
·
 ;
;

А: "Точка попала внутрь треугольника".

 =0,41
=0,41
Ответ: 0,41
2.4. Сумма событий
Определение 2.8. Суммой событий А1, А2,
..., Аn называется событие А = А1+А2+ ...+ Аn,состоящее в наступлении хотя бы
одного из событий А1, А2, ..., Аn.
Например, два стрелка стреляют в одну и ту же мишень по одному разу. Обозначим события:
А1: "1-й стрелок попал в мишень",
А2: "2-й стрелок попал в мишень".
Тогда их суммой будет событие А: "Мишень поражена", то есть, либо
попал только 1-й стрелок, либо только 2-й, либо попали оба.
Если события А1, А2, ..., Аn несовместимы, то одновременно они наступить не могут и определение
будет следующим.
Определение 2.9.
Суммой несовместимых событий А1, А2, ..., Аn
называется событие А, состоящее в наступлении только одного из событий А1, А2, ..., Аn.
Рассмотрим для простоты два несовместимых события А и В. Пусть m -число благоприятных исходов для события А,
k-число благоприятных исходов для события В, n -общее число исходов.
Вероятности событий А и В будут  Число исходов, благоприятных для события С = А+В
равно m+k, так как они несовместимы и
Число исходов, благоприятных для события С = А+В
равно m+k, так как они несовместимы и
 Вероятность суммы несовместимых событий равна сумме их
вероятностей.
Вероятность суммы несовместимых событий равна сумме их
вероятностей.
 (2.3)Формула (2.3) допускает обобщение на любое число попарно
несовместимых событий.
(2.3)Формула (2.3) допускает обобщение на любое число попарно
несовместимых событий.
Пример 45.
Брошены две игральных кости. Какова вероятность, что сумма очков на выпавших гранях будет не меньше 10?
Решение.
В данном испытании фраза "не меньше 10" означает, что
выпадет 10, или 11, или 12 очков. Все три эти события
несовместимы, поэтому вероятность их суммы равна
сумме вероятностей. Из 36 исходов 3 будут благоприятствовать
выпадению 10 очков. Это: (4,6); (5,5) и (6,4). 11 очков
могут выпадать двумя способами: (5,6) и (6,5), а 12 очков -
только одним способом. Итак, если обозначить
А: "Выпадение в сумме 10 очков", P(A)= 3/36,
В: " -- // -- // -- // -- 11 - //- ",P(B)= 2/36,
С: " -- // -- // -- // -- 12 - //- ",P(C)= 1/36.
D: "Выпадение не меньше 10 очков".
P(D)=P(A) + P(B) +P(C)= 3/36 + 2/36 +1/36 = 6/36 =1/6.
Ответ :1/6.
2.5. Произведение событий
Определение 2.10.
Два события А и В называются
независимыми, если вероятность одного из них не зависит от того, произошло или
не произошло другое.
Определение 2.11.
Произведением независимых событий А и В
называется событие С = А·В, заключающееся в том, что
произошло и событие А, и событие В.
Рассмотрим два независимых события А и В. Пусть событию
А благоприятствуют m исходов из общего
числа n исходов P(A)= m / n. Событию В - соответственно
k и l исходов P(B)= k / l.Тогда для события С = А·В по
правилу произведения благоприятных исходов будет m · k,
а общее число - n · l.
 Вероятность произведения независимых событий
равна произведению их вероятностей.
P(AB)=P(A)·P(B) (2.4)
Например, вероятность выпадения двух гербов при
бросании двух монет будет равна 0,5 · 0,5 = 0,25, а
вероятность появления трех шестерок подряд при трех
бросках игральной кости 1/6·1/6·1/6= 1/216.
Вероятность произведения независимых событий
равна произведению их вероятностей.
P(AB)=P(A)·P(B) (2.4)
Например, вероятность выпадения двух гербов при
бросании двух монет будет равна 0,5 · 0,5 = 0,25, а
вероятность появления трех шестерок подряд при трех
бросках игральной кости 1/6·1/6·1/6= 1/216.
2.6. Вероятность суммы совместимых событий
Рассмотрим два совместимых события А и В. Пусть m - число исходов, благоприятных для события А, k -число
исходов, благоприятных для события В. И пусть среди этих m+k исходов l благоприятствуют и А, и В
одновременно. Если n - общее число равновозможных событий, образующих полную группу, то
 Событие А+В заключается в том, что происходит либо событие А,
либо событие В, либо А и В вместе. Ему благоприятствуют m+k-l исходов, следовательно,
Событие А+В заключается в том, что происходит либо событие А,
либо событие В, либо А и В вместе. Ему благоприятствуют m+k-l исходов, следовательно,
 Вероятность суммы двух совместимых событий равна сумме вероятностей этих событий без вероятности их
совместного наступления.
P(A+B)=P(A)+P(B)-P(AB) (2.5)
Пример 46.
Вероятность поражения цели первым орудием равна 0,7,вторым - 0,8. Найти вероятность поражения цели при залпе
из двух орудий.
Вероятность суммы двух совместимых событий равна сумме вероятностей этих событий без вероятности их
совместного наступления.
P(A+B)=P(A)+P(B)-P(AB) (2.5)
Пример 46.
Вероятность поражения цели первым орудием равна 0,7,вторым - 0,8. Найти вероятность поражения цели при залпе
из двух орудий.
Решение.
Пусть А: "Попадание из 1 орудия",
В: "Попадание из 2 орудия",
С: "Цель поражена". А и В - совместимые события, так как
они могут произойти одновременно. По формуле (2.5)
P(C)=P(A) + P(B) - P(AB) = 0,7 + 0,8 - 0,7 · 0,8 = 0,94
Ответ: 0,94
2.7 Условные вероятности
При совместном рассмотрении двух событий А и В часто возникает вопрос, насколько связаны эти события друг
с другом. Если наступление события В влияет на вероятность события А, то события А и В называются зависимыми.
Определение 2.12.
Условной вероятностью Р(А/В) называется
вероятность события А при условии, что уже произошло событие В.
Пример 47.
Из урны, содержащей 8 белых и 12 черных шаров наугад друг за
другом вынимают два шара. Даны события: А: "Первый шар - белый",
В: "Второй шар -белый". Найти условные вероятности
 Решение.
Во-первых, заметим, что
Решение.
Во-первых, заметим, что  : "Первый шар - черный",
: "Первый шар - черный", : "Второй шар - черный". Найдем P(B/A).
Событие А уже произошло, то есть первый шар вынут и он - белый.
Требуется найти вероятность того, что второй шар - белый. В урне осталось 19 шаров, из них 7 белых. Поэтому
P(B/A)= 7/19. Рассуждая аналогично, находим:
: "Второй шар - черный". Найдем P(B/A).
Событие А уже произошло, то есть первый шар вынут и он - белый.
Требуется найти вероятность того, что второй шар - белый. В урне осталось 19 шаров, из них 7 белых. Поэтому
P(B/A)= 7/19. Рассуждая аналогично, находим:

2.8 Вероятность произведения зависимых событий
Пусть даны два зависимых события А и В. И из n равновозможных
исходов событию А благоприятствуют m,событию В-k,событию АВ-r исходов
(r m,r
m,r ).
).
P(A)=m / n; P(B)=k / n; P(AB)=r / n.
Если произошло событие А, то реализовался один из m исходов, благоприятствующих А. Вероятность того, что при этом условии
произошло событие В найдется, как условная вероятность
 Отсюда
P(AB)=P(A)·P(B/A).
Отсюда
P(AB)=P(A)·P(B/A).
Это и есть правило умножения зависимых
событий.
Вероятность произведения двух зависимых событий
равна произведению вероятности одного из них на условную
вероятность другого при условии, что первое произошло.
P(AB)=P(A)·P(B/A) (2.6)
2.9 Формула полной вероятности.
Пусть нам требуется найти вероятность события А, которое
происходит вместе с одним из попарно несовместимых событий
Н1, Н2, ..., Нn, образующих
полную группу. События Н1, Н2, ..., Нn
будем называть гипотезами. Имеем А = АН1 + АН2 +
... + АНn , причем АН1, АН2,
... АНn попарно несовместимы. Применяя формулы (2.3) и (2.6),
получим:
 (2.7)
(2.7)
Это есть формула полной вероятности. С ее помощью решается
широкий класс задач.
Пример 48.Имеются
3 одинаковых коробки, содержащие по 20 лампочек. В 1-й коробке
из них 2 бракованные лампочки, во второй - 4, в третьей - 5.
Наугад выбирается коробка, а из нее наугад одна лампочка.
Какова вероятность, что эта лампочка бракованная?
Решение.
А: "Взята бракованная лампочка". Возникают 3 ги-потезы:
Н1:"Выбрана 1-я коробка",
Н2:"Выбрана 2-я коробка",
Н3:"Выбрана 3-я коробка".Поскольку все коробки одинаковые,
P(H1)=P(H2)=P(H3)=1 / 3.Находим условные вероятности.
 По формуле полной вероятности
По формуле полной вероятности

Ответ: 0,18
Пример 49.Из
полного набора костей домино извлечена одна кость. Найти вероятность того, что вторую наугад извлеченную
кость можно приставить к первой согласно правилам игры.
Решение.
А: "Вторую кость можно приставить к первой". Если первая кость окажется дублем, вероятность события А
будет меньше, чем если бы она была не дублем.
Поэтому возникают две гипотезы:
Н1:"Первая кость-дубль",
Н2:"Первая кость-не дубль".
Находим:
Если первая кость - дубль, то найдутся 6 из 27 оставшихся
костей, которые можно приставить к первой, а если не дубль,
то их будет 12. Поэтому По формуле полной вероятности
По формуле полной вероятности

Ответ: 7/18.
2.10 Формула Байеса
В тесной связи с формулой полной вероятности находится формула Байеса. Она относится к той же ситуации, когда событие А наступает только вместе с одной из гипотез и
позволяет оценить вероятность гипотезы после того, как событие А произошло.
Пусть произведен опыт и наступило событие А. Мы не можем с точностью сказать, какая из гипотез осуществилась,
однако можем найти вероятность каждой из них. По формуле (2.6)
P(AHi)=P(A)·P(Hi/A) =
P(Hi)·P(A/Hi).Отсюда
 (2.8)
Это и есть формула Байеса. Здесь Р(А) находится по
формуле полной вероятности, Hi (i=1,2,...,n)
- любая из гипотез, а Р(Нi/А) - вероятность этой гипотезы при условии, что произошло событие А.
(2.8)
Это и есть формула Байеса. Здесь Р(А) находится по
формуле полной вероятности, Hi (i=1,2,...,n)
- любая из гипотез, а Р(Нi/А) - вероятность этой гипотезы при условии, что произошло событие А.
Пример 50.
В трех одинаковых ящиках находятся 6 белых и 4 черных, 7 белых и 3 черных, 8 белых шаров соответственно. Из
произвольного ящика наугад выбирается один шар. Он оказался белым.
Какова вероятность, что этот шар вынут из второго ящика?
Решение.
Пусть Н1,Н2,Н3- три гипотезы, что выбран 1-й, 2-й, 3-й ящик. Требуется
найти вероятность второй гипотезы при условии, что
событие А произошло, т.е. P(H2/A).По формуле
Байеса
 Ответ: 7 / 23.
Ответ: 7 / 23.
2.11. Формула Бернулли
Пусть проводится n независимых испытаний, в каждом из
которых с одной и той же вероятностью p может появиться
некоторое событие А. Поставим задачу: найти вероятность
того, что в этих n испытаниях событие А появится ровно
m раз. Обозначим А1 - появление события А
в 1-м испытании, А2 - во 2-м испытании, и
так далее. Непоявление события А в 1-м испытании
обозначим  ,
во 2-м
,
во 2-м  и т.д.
Событие, состоящее в появлении события А m раз в n
испытаниях представится в виде суммы произведений вида
и т.д.
Событие, состоящее в появлении события А m раз в n
испытаниях представится в виде суммы произведений вида
 . Если обозначить
вероятность непоявления события А через q ,то вероятность
каждого такого произведения равна, pm · qn-m,а
всего их будет
. Если обозначить
вероятность непоявления события А через q ,то вероятность
каждого такого произведения равна, pm · qn-m,а
всего их будет штук.
Получим:
штук.
Получим: (2.8)
Это - формула Бернулли. Здесь обозначено: Pn(m)
вероятность появления события А m раз в n испытаниях,
р - вероятность появ-ления события А в одном испытании,
q = 1 - p.
(2.8)
Это - формула Бернулли. Здесь обозначено: Pn(m)
вероятность появления события А m раз в n испытаниях,
р - вероятность появ-ления события А в одном испытании,
q = 1 - p.
Пример 51.
Вероятность попадания в цель при одном выстреле равна 0,8.
Найти вероятность пяти попаданий при шести выстрелах.
Решение.
n =6, m =5, p =0,8, q = 1 - 0,8 = 0,2.
Ответ: 0,39
Пример 52.
Вы играете в шахматы с равным по силе партнером. Чего следует
больше ожидать: 3 побед в 4 партиях или 5 побед в 8 партиях?
Решение.
р = 0,5; q = 0,5.


Ответ: P4(3) > P8(5)
2.12 Случайные величины.
Очень часто в результате опыта в качестве случайного события
появляется некоторое число. Так при бросании игральной
кости выпадает определенное число очков, при обследовании
партии готовых деталей обнаруживается некоторое число
бракованных и т.д.
Определение 2.13.
Случайной величиной, связанной с данным
опытом, называется величина, которая при каждом осуществлении
этого опыта принимает то или иное числовое значение, заранее
неизвестно, какое именно.
Приведем несколько примеров случайных величин.
1.Приобретено несколько лотерейных билетов.
Х - количество выигравших билетов.
2.Испытывается электрическая лампочка на длительность
горения. Х - время горения до выхода из строя.
3.Число автомобилей, проезжающих по улице за 1 час.
Если количество возможных значений случайной величины
конечно, она называется дискретной, а если возможные значения
заполняют некоторый числовой промежуток, то - непрерывной.
Так в приведенных выше примерах 1 и 3 случайные величины
- дискретные, а в примере 2 - непрерывная. Для полного
описания случайной величины недостаточно знать, какие значения
она принимает, необходимо еще оценить, как часто она принимает
то или иное значение. Для изучения дискретной случайной
величины составляют так называемый закон распределения. Это
таблица, в которую занесены все возможные значения случайной
величины и их вероятности. В качестве примера составим закон
распределения случайной величины Х - суммы очков при
однократном бросании двух игральных костей.
| X | 2 |
3 | 4 |
5 | 6 |
7 | 8 |
9 | 10 |
11 | 12 |
| P |
1 / 36 | 2 / 36 |
3 / 36 | 4 / 36 |
5 / 36 | 6 / 36 |
5 / 36 | 4 / 36 |
3 / 36 | 2 / 36 |
1 / 36 |
Если закон распределения составлен правильно, сумма
вероятностей всех значений должна равняться 1.
2.13. Числовые характеристики случайной величины.
Пусть дискретная случайная величина Х имеет
распределена по закону:
| X |
x1 | x2 |
x3 | .... |
xn |
| P |
p1 | p2 |
p3 | ..... |
pn |
Опреденление 2.14.
Математическим ожиданием М(Х) дискретной
случайной величины Х называется сумма произведений возможных значений
на их вероятности.
М(Х) = х1р1 + х2р2
+ ... + хnpn (2.10) Теоретико-вероятностный смысл этой
характеристики состоит в том, что математическое ожидание
приближенно равно среднему арифметическому всех ее значений
при достаточно большом числе испытаний. Математическое
ожидание обладает также следующими свойствами:
1.Математическое ожидание постоянной величины
равно самой этой постоянной.
М(с) = с
2.Постоянный множитель можно выносить за знак
математического ожидания.
М(сХ) = сМ(Х)
3. Математическое ожидание суммы двух случайных
величин равно сумме их вероятностей.
М(Х + Y) = М(Х) + М(Y)
4. Математическое ожидание разности двух случайных
величин равно разности их вероятностей.
М(Х - Y) = М(Х) - М(Y)
Математическое ожидание не дает полной
характеристики закона распределения. Так, например, даны две случайных
величины Х и Y следующими законами распределения:
| X | -2 |
0 | 2 |
| |
Y | -50 |
0 | 50 |
| p | 0,4 |
0,2 | 0,4 |
| |
p | 0,3 |
0,4 | 0,3 |
Математические ожидания их равны М(Х) = М(Y) = 0,однако возможные значения рассеяны поразному: у случайной величины Y
они сильнее отклоняются от среднего значения М(Y). И на практике, приодинаковой средней величине годовых осадков одна местность может быть
благоприятной для земледелия, другая - нет. Поэтому возникает необходимость введения новых
числовых характеристик случайной величины, по которым можно судить
о рассеянии возможных значений около математического ожидания. Этими
характеристиками являются дисперсия D(X) и среднее квадратическое
отклонение
Опреденление 2.15.Дисперсией дискретной случайной величины Х
называется математическое ожидание квадрата ее отклонения.
D(X) = M[X -M(X)]2 (2.11)
Опреденление 2.16. Средним квадратическим отклонением дискретной
случайной величины Х называется квадратный корень из ее дисперсии.
 (2.12)
Дисперсия обладает следующими свойствами, которые непосредственно получаются
из формулы (2.11).
(2.12)
Дисперсия обладает следующими свойствами, которые непосредственно получаются
из формулы (2.11).
1.Дисперсия равна разности между математическим
ожиданием квадрата случайной величины Х и квадратом ее математического
ожидания.
D(X) = M(X2) - M2(X) (2.13)
2.Дисперсия постоянной величины равна нулю.
D(c) = 0
3.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
D(cX) = c2D(X)
4.Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий.
D(X + Y) = D(X) + D(Y)
5. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий.
D(X - Y) = D(X) + D(Y)
Пример 53. Испытывается устройство, состоящее из четырех одинаковых приборов. Вероятность отказа каждого прибора равна 0,2. Составить закон распределения, найти математическое ожидание, дис-персию и среднее квадратическое отклонение случайного числа отка-завших приборов.
Решение.Х - число отказавших приборов. Возможные значе-ния этой случайной величины 0, 1, 2, 3, 4. Их вероятности находим
по формуле Бернулли  при n=4, p=0,2, q=0,8.
при n=4, p=0,2, q=0,8.
 Проверка: 0,4096+0,4096+0,1536+0,0256+0,04016=1. Закон распределения будет иметь вид:
Проверка: 0,4096+0,4096+0,1536+0,0256+0,04016=1. Закон распределения будет иметь вид:
| X | 0 |
1 | 2 |
3 | 4 |
| p | 0,4096 |
0,4096 | 0,1536 |
0,0256 | 0,0016 |
М(Х)=0,4096·0+0,4096·1+0,1536·23+0,0256·3+0,0016·4=0,8;
D(Х)=M(X2)-M2(X)=04096·02
+0,4096·12+0,1536·22+0,0256·32
+0,0016·42-0,82=0,64
s(X)= = 0,8.
= 0,8.
Ответ: М(Х)=0,8;D(Х)=0,64; s(Х)=0,8.
Пример 54. Круглая мишень разделена
диаметрами на 8 равных секторов и вращается вокруг оси О. При достаточно большой скорости
вращения стрелок не может различать секторы и вынужден стрелять наугад. При попадании в
1-й сектор он выигрывает 1 руб., во 2-й - выигрывает 2 руб. и т.д., при попадании в 8-й сектор -
выигрывает 8 руб. Выгодно ли стрелку участвовать в такой игре, если за каждый выстрел
надо платить 5 руб.?
Решение.Пусть случайная величина
Х - размер выигрыша стрелка при одном выстреле. Так как все секторы одинаковы, вероятность
попадания в каждый равны по 1\8. Найдем математическое ожидание выигрыша.
M(X)=1/8 (1+2+3+4+5+6+7+8)=4,5(руб.).Это среднее значение выигрыша в данной игре, которое
совпадает со "справедливой ценой" одного выстрела. Так как за выстрел приходится платить 5 руб.,
то стрелять много раз невыгодно.
Пример 55. У охотника 4
патрона. Он стреляет по зайцу, пока не попадет или пока не кончатся патроны. Составить
закон распределения числа израсходованных патронов, если вероятность его попадания при
одном выстреле равна 0,6. Найти М(Х), D(Х), s(Х).
Решение.. Х - число
израсходованных патронов. Возможные значения Х = 1, 2, 3, 4. Находим их вероятности.
Р(Х=1) = 0,6;
Р(Х=2) = 0,24;
Р(Х=3) = 0,4·0,4· 0,6 = 0,096;
Р(Х=4) = 0,4 · 0,4· 0,4 · 0,6 + 0,4 · 0,4 · 0,4 · 0,4 = 0,064.
Проверка: 0,6 + 0,24 + 0,096 + 0,064 = 1. Закон распределения Х:
| X | 1 |
2 | 3 |
4 |
| p | 0,6 |
0,24 | 0,096 |
0,064 |
М(Х) = 0,6 · 1 + 0,24 · 2 + 0,096 ·3 + 0,064 · 4 = 1,624;
D(Х) = 0,6· 12 + 0,24· 22 + 0,096 · 32 +
0,064 · 42 - 1,6242 = 0,81;
s(Х)=
Ответ: М(Х) = 1,624; D(Х) = 0,81;s (Х) = 0,9.
 (2.1)
(2.1) (2.1)
(2.1)
 . Если общее число исходов некоторого испытания равно n и событию А благоприятствуют m исходов, то, очевидно, событию
. Если общее число исходов некоторого испытания равно n и событию А благоприятствуют m исходов, то, очевидно, событию
 благоприятствуют n -m исходов,
благоприятствуют n -m исходов,
 ,следовательно,
,следовательно,
 (2.2)
(2.2) .
Оно называется относительной частотой события А. Эта частота
обладает свойством устойчивости: с увеличением количества опытов она приближается к некоторому постоянному числу,
стабилизируясь около него. Данный факт служит основой для еще одного определения вероятности - статистического.
.
Оно называется относительной частотой события А. Эта частота
обладает свойством устойчивости: с увеличением количества опытов она приближается к некоторому постоянному числу,
стабилизируясь около него. Данный факт служит основой для еще одного определения вероятности - статистического.
 .Это число и принимают приближенно за вероятность нормальной работы станка.
.Это число и принимают приближенно за вероятность нормальной работы станка.

 .
Геометрическое определение вероятности события формулируется следующим образом.
.
Геометрическое определение вероятности события формулируется следующим образом.
 . Найдем n - общее число исходов. Если мы раскладываем 6 карточек
в ряд, то число всевозможных вариантов будет равно количеству
перестановок из шести элементов:
. Найдем n - общее число исходов. Если мы раскладываем 6 карточек
в ряд, то число всевозможных вариантов будет равно количеству
перестановок из шести элементов:
 .
.

 , m =1,
, m =1,
 .
.

 Число благоприятных исходов в первом случае
Число благоприятных исходов в первом случае
 , во втором - по правилу суммы
, во втором - по правилу суммы  = 73,
в третьем - по правилу произведения m = 10 · 8 = 80.
Находим:
= 73,
в третьем - по правилу произведения m = 10 · 8 = 80.
Находим: 
 Для нахождения m заметим, что 2 красных карандаша из 5 красных можно выбрать
Для нахождения m заметим, что 2 красных карандаша из 5 красных можно выбрать
 способами, а 1 зеленый из 7 зеленых -
способами, а 1 зеленый из 7 зеленых - способами.
И, по правилу произведения,
способами.
И, по правилу произведения, Итак,
Итак,

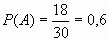

 ·
·
 ;
;

 =0,41
=0,41
 Число исходов, благоприятных для события С = А+В
равно m+k, так как они несовместимы и
Число исходов, благоприятных для события С = А+В
равно m+k, так как они несовместимы и

 (2.3)
(2.3)
 Событие А+В заключается в том, что происходит либо событие А,
либо событие В, либо А и В вместе. Ему благоприятствуют m+k-l исходов, следовательно,
Событие А+В заключается в том, что происходит либо событие А,
либо событие В, либо А и В вместе. Ему благоприятствуют m+k-l исходов, следовательно,


 : "Первый шар - черный",
: "Первый шар - черный", : "Второй шар - черный". Найдем P(B/A).
Событие А уже произошло, то есть первый шар вынут и он - белый.
Требуется найти вероятность того, что второй шар - белый. В урне осталось 19 шаров, из них 7 белых. Поэтому
P(B/A)= 7/19. Рассуждая аналогично, находим:
: "Второй шар - черный". Найдем P(B/A).
Событие А уже произошло, то есть первый шар вынут и он - белый.
Требуется найти вероятность того, что второй шар - белый. В урне осталось 19 шаров, из них 7 белых. Поэтому
P(B/A)= 7/19. Рассуждая аналогично, находим:

 m,r
m,r ).
).
 Отсюда
P(AB)=P(A)·P(B/A).
Отсюда
P(AB)=P(A)·P(B/A). (2.7)
(2.7)


 По формуле полной вероятности
По формуле полной вероятности
 (2.8)
(2.8)

 ,
во 2-м
,
во 2-м  и т.д.
Событие, состоящее в появлении события А m раз в n
испытаниях представится в виде суммы произведений вида
и т.д.
Событие, состоящее в появлении события А m раз в n
испытаниях представится в виде суммы произведений вида
 . Если обозначить
вероятность непоявления события А через q ,то вероятность
каждого такого произведения равна, pm · qn-m,а
всего их будет
. Если обозначить
вероятность непоявления события А через q ,то вероятность
каждого такого произведения равна, pm · qn-m,а
всего их будет штук.
Получим:
штук.
Получим: (2.8)
(2.8)

 (2.12)
(2.12) при n=4, p=0,2, q=0,8.
при n=4, p=0,2, q=0,8.

 = 0,8.
= 0,8.

