Решение задач

Комбинированный метод

Задача 2. На ребрах А1В1 и DD1 параллелепипеда АВСDА1В1С1D1 взяты соответственно точки Р и S, а в гранях CC1D1D и АА1D1D соответственно точки Q и R. Построить сечение параллелепипеда плоскостью, проходящей через точку S параллельно плоскости РQR.

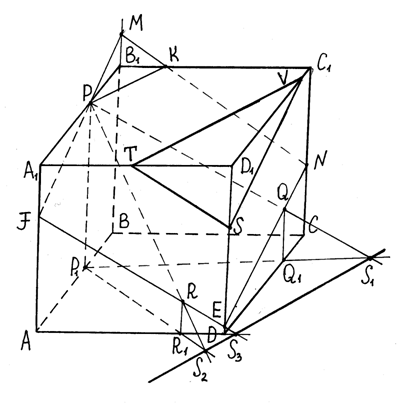
Решение:

1. Проектируем данные точки на плоскость нижнего основания параллелепипеда, получаем точки Р1, Q1, R1. Находим точку S1, полученную при пересечении прямых РQ и Р1Q1. Находим точку S2, полученную при пересечении прямых PR и P1R1. Прямая S1S2 - след секущей плоскости.

2. Находим точку S3, полученную при пересечении прямых AD и S1S2. Прямая S3R при пересечении с прямой DD1 дает точку Е. Пересечение прямых S3R и АА1 дает точку F.

3. Найдем точку М, в которой пересекаются прямые FP и ВВ1. Точка N получается при пересечении прямых EQ и СС1.

4. Точку К получаем при пересечении прямых NM и В1С1.

5. Строим вспомогательное сечение EFPKN, соединяя последовательно точки.

6. В плоскости АА1D1D проведем прямую ST параллельно прямой EF.

7. В плоскости СС1D1D проведем прямую SV параллельно прямой EN.

8. Треугольник STV - искомое сечение.