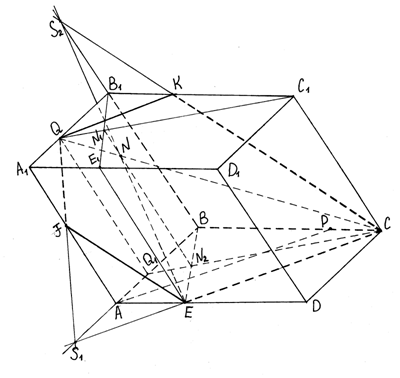
Решение:
1. Проводим прямые АР и СQ. Так как искомое сечение должно проходить через прямую СQ, параллельно прямой АР, то в плоскости АВСD проведем прямую СS1 параллельно АР. Прямая СS1 - след секущей плоскости, она пересекает прямую AD в точке Е.
2. При пересечении прямых АА1 и QS1 получаем точку F.
3. Находим прямую N1N2, полученную при пересечении плоскостей СC1QQ1 и ВВ1Е1Е. Найдем точку N, в которой пересекаются прямые N1N2 и CQ.
4. В плоскости ВВ1Е1Е находим точку S2, полученную при пересечении прямых ЕN и ВВ1.
5. На ребре В1С1 получаем точку К при пересечении с прямой СS2.
6. Соединяя последовательно точки, получаем многоугольник СЕFQK - искомое сечение.