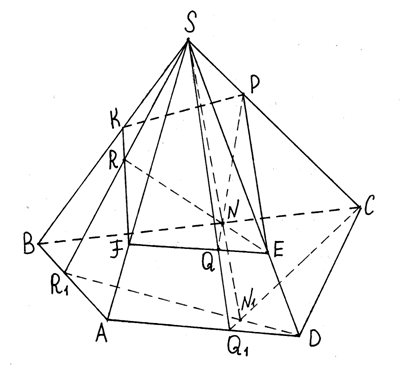
Решение:
1. Построим вспомогательное сечение пирамиды плоскостью, проходящей через точку S и прямые SQ 1 и SC, т. е. плоскость SCQ1.
2. Будем искать след плоскости PQR на прямой SD. Для этого построим второе вспомогательное сечение пирамиды. Полученное сечение SDR1 - сечение, проходящее через прямые SR1 и SD, на котором находим след секущей плоскости PQR.
3. Строим прямую SN1, по которой пересекаются плоскости SCQ1 и SDR1, и затем точку N, в которой пересекаются прямые PQ и SN1.
4. Так как точка N лежит на прямой PQ, то она лежит и в секущей плоскости PQR. Тогда прямая RN лежит в секущей плоскости, а также и точка Е - точка пересечения прямых RN и SD.
5. Проведем прямую EQ, она пересекает прямую SA в точке F, которая является следом секущей плоскости на ребре SA.
Многоугольник ЕFКР - искомое сечение.