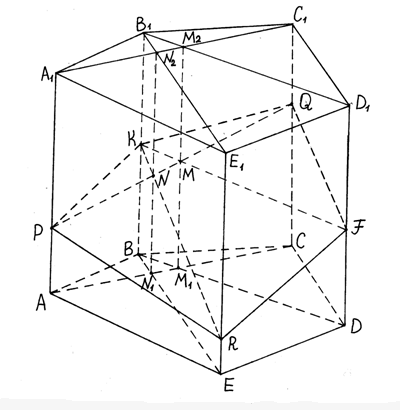
Решение:
1. Построим первое вспомогательное сечение призмы - ее сечение плоскостью, которая проходит через прямые АА1 и QQ1. Этим сечением является четырехугольник АА1С1С.
2. Построим второе вспомогательное сечение, которое проходит через прямые ВВ1 и ЕЕ1 - плоскость ВВ1Е1Е.
3. Находим прямую N1N2, по которой пересекаются плоскости вспомогательных сечений АА1С1С и ВВ1Е1Е, а затем точку N, в которой пересекаются прямые PQ и N1N2.
4. Так как точка N лежит на прямой PQ, то она лежит и в плоскости PQR. Это значит, что точка К, в которой пересекаются прямые RN и ВВ1.
5. Построим прямую М1М2, по которой пересекаются плоскости ВВ1Е1Е и АА1СС, а затем точку М - точку пересечения прямых PQ и М1М2. Проведя прямую КМ, получаем на прямой DD1 - точку F, след секущей плоскости PQR.
6. Соединяя заданные и построенные точки получаем многогранник PKQFR - искомое сечение.