Решение задач

Метод внутреннего проектирования

Задача 2. Точки Р, Q, R взяты на поверхности параллелепипеда АВСDА1В1С1D1 следующим образом: точка Р лежит на грани СС1D1D, точка Q - в грани АА1D1D, а точка R - в плоскости грани АА1В1В. Построить сечение параллелепипеда плоскостью РQR.

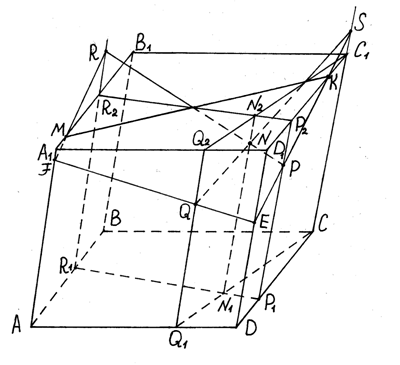
Решение: 1. Построим плоскость РР1R1R, определяемую параллельными прямыми РР1 и RR1, и плоскость СС1Q2Q1, определяемую параллельными прямыми СС1 и Q1Q2. 2. Построим прямую N1N2, по которой пересекаются две построенные плоскости. 3. Найдем точку N, в которой пересекаются прямые PR и N1N2. 4. В плоскости СС1Q2Q1 проведем прямую QN и найдем точку S - точку пересечения с прямой СС1. 5. В плоскости СС1D1D проведем прямую SP и найдем точки Е и К, в которых прямая SP пересекает прямые С1D1 и DD1. 6. В плоскости АА1D1D проведем прямую EQ и найдем точку F, в которой прямая EQ пересекает прямую АА1. 7. В плоскости АА1В1В проведем прямую FR и найдем точку М, в которой прямая FR пересекает прямую А1В1. 8. В плоскости А1В1С1D1 построим прямую МК. 9. Четырехугольник ЕFМК - искомое сечение.