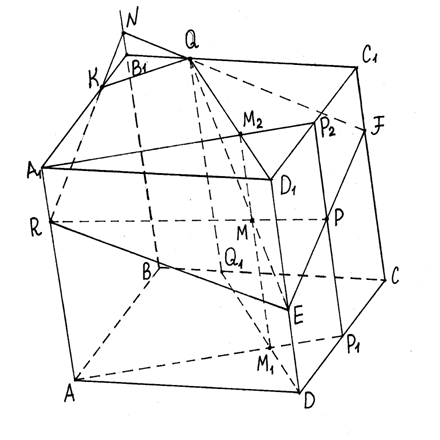
Решение:
1. Построим плоскость АА1Р1Р, определяемую параллельными прямыми АА1 и РР1, и плоскость DD1QQ1, определяемую параллельными прямыми QQ1 и DD1.
2. Найдем прямую М1М2, по которой пересекаются две построенные плоскости.
3. Найдем точку М, в которой пересекаются прямые РR и ММ1.
4. В плоскости DD1QQ1 проведем прямую QM и найдем точку Е - точку ее пересечения с прямой DD1.
Итак, на ребре DD1 найдена точка, принадлежащая секущей плоскости. Далее легко находятся точки пересечения других ребер с секущей плоскостью.
5. В плоскости СС1D1 D проведем прямую EР, которая при пересечении с прямой СС1 дает точку F.
6. В плоскости ВВ1С1C проведем прямую FQ и найдем точку N, в которой прямая FQ пересекает прямую ВВ1.
7. В плоскости АА1В1В проведем прямую RN и найдем точку К, в которой она пересекается с прямой А1В1.
8. Многоугольник EFQKR - искомое сечение.