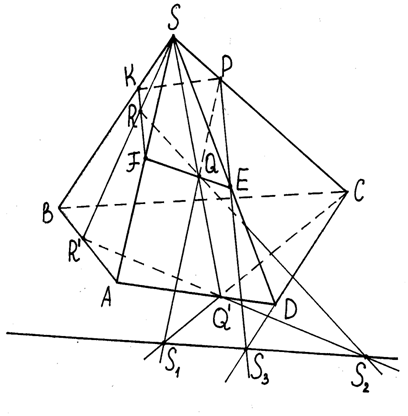
1. Построим след секущей плоскости PQR. Для этого спроектируем точки Р, Q и R на плоскость ABCD из точки S. Получим точку Р1 (совпадает с точкой С) и точки Q1 и R1. Затем найдем две точки следа плоскости PQR, точку S1 - точку пересечения прямых PQ и CQ1 и точку S2 - точку пересечения прямых RQ и R1Q1. Прямая S1S2 - след секущей плоскости.
2. Построим след секущей плоскости на прямой SD. Для этого найдем точку S3, в которой СD пересекает след S1S2, проведем прямую S3Р. Точка Е, в которой прямая S3Р пересекает прямую SD, и является следом секущей плоскости на прямой SD.
3. Дальнейшие построения можно выполнить, уже не пользуясь следом S1S2. Так как точки Е и Q обе лежат в секущей плоскости, и в плоскости SAD, то прямая ЕQ является линией пересечения этих плоскостей. На прямой SA строим точку F, в которой пресекаются прямые EQ и SA.
4. Рассуждая аналогично, получаем далее FK - след секущей плоскости на грани SAВ и КР - след секущей плоскости на грани SBC.
5. Многоугольник ЕFКР - искомое сечение.