В работе Г.Г. Михайличенко [1] были найдены метрические функции одномерных и двумерных феноменологически симметричных геометрий. Метрическая функция одномерной геометрии обозначается f(ij), где пара 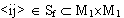, а метрическая функция двумерной геометрии --- f(ij), где 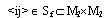, причем выполняется свойство существенной зависимости от координат (не существует такой замены координат, которая бы привела к уменьшению числа переменных). Выполняется также аксиома феноменологической симметрии: одномерные геометрии: для любых трех точек i,j,k таких, что имеет место функциональная связь:

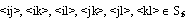
двумерные геометрии: для любых четырех точек i,j,k,l таких, что 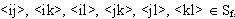имеет место функциональная связь:

Оказывается, что существует всего одна одномерная феноменологически симметричная геометрия с метрической функцией:

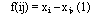
где, например, x_i --- координата точки i, и десять двумерных феноменологически симметричных геометрий, среди которых:

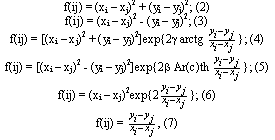
где 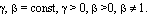(2) - метрическая функция (МФ) плоскости Евклида, (3) - МФ плоскости Минковского, (4) - МФ собственно гельмгольцевой плоскости, (5) - МФ псевдогельмгольцевой плоскости, (6) - МФ дуальногельмгольцевой плоскости и (7) - МФ симплициальной плоскости. Г.Г. Михайличенко доказывается, что метрическая функция (1) допускает однопараметрическую группу движений, по которой она восстанавливается, а МФ (2) --- (7) --- трехпараметрические группы движений, по которым они также восстанавливаются [1].

Цель нашего исследования состоит в установлении свойства феноменологической симметрии (ФС) метрической функции

от пары МФ одномерной феноменологически симметричной геометрии. Эту проблему будем решать групповыми методами. Оператор алгебры Ли группы движений пространства с МФ (8) представим в виде:

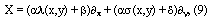
где 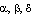-- произвольные постоянные. Очевидно, базисными операторами алгебры Ли являются следующие:

По базисным операторам (9') можно восстановить МФ (8), а по МФ (8) --- эти операторы. Таким образом, имеет место функционально-дифференциальное уравнение:

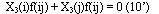
или в координатах

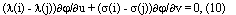
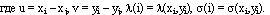
Напомним, что МФ f(ij) является невырожденной, если для любых трех точек i, j, k якобиан

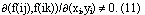
Лемма 1.Если в уравнении (10) 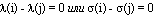, то непостоянная метрическая функция (8) не является феноменологически симметричной.

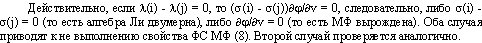
Лемма 2.Условие невырожденности (11) непостоянной МФ (8) со свойством феноменологической симметрии можно записать в виде:

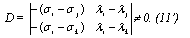
Действительно, рассмотрим МФ(8) со свойством ФС. По лемме1 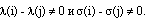Тогда из уравнения (10) . Поэтому 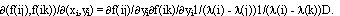Из этого равенства следует, что если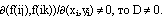

Лемма 3.

Если в уравнении (10) 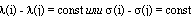, то непостоянная метрическая функция (8) не является феноменологически симметричной.

Действительно, если Поэтому Значит, по лемме 1 метрическая функция (8) не является феноменологически симметричной. Случай 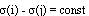рассматривается аналогично.

Приступим теперь к доказательству основных теорем.

Теорема 1.Непостоянная метрическая функция 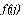(решение уравнения (10)) является ФС тогда и только тогда, когда якобиан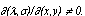

Докажем сначала обратное утверждение. Предположим противное, то есть, что непостоянная МФ не является ФС. Тогда решением уравнения (10) является либо вырожденная МФ (равен нулю якобиан 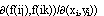, либо невырожденная. В первом случае, либо (следствие условия непостоянства МФ), либо , следовательно, определитель (11') равен 0. Первые два варианта, очевидно, приводят к 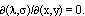Рассмотрим третий вариант. Расписывая определитель (11'), приходим к равенству 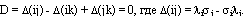Дифференцируя последнее уравнение по xi и yi, получаем систему линейных уравнений относительно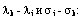

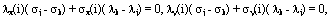
которая совместна тогда и только тогда, когда, либо , либо 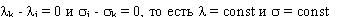. Во втором случае по МФ не восстанавливается трехпараметрическая группа движений. Поэтому 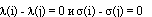Итак, если МФ не является ФС, то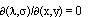

Докажем теперь прямое утверждение. Предположим противное, то есть, что якобиан 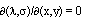. Тогда либо 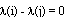и по лемме 1 МФ не является феноменологически симметричной, либо 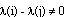. Рассмотрим тождество

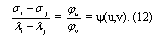
Продифференцируем уравнение (12) по координатам точек i и j, после простых преобразований, приходим

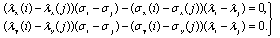
Данную систему можно рассмотреть как линейную относительно разностей 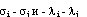. Обозначим определитель этой системы:

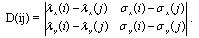
Лемма 4.Если якобиан 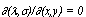, то определитель D(ij) = 0.

Из соотношения 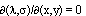следует, что 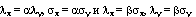. Подставляя найденное в уравнение

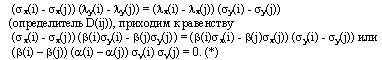
Если 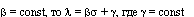. Следовательно, уравнение (10) примет вид: 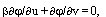то есть интегралом является МФ без свойства ФС: 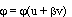. Если теперь 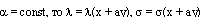. Обозначим для удобства p = x_i + ay_i, q = x_j + ay_j. Подставляя найденное в первое уравнение выше выписанной линейной системы, приходим к тождеству:

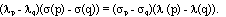
Дифференцируя это тождество по переменным p и q, получаем

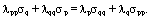
Очевидно, 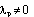(начало доказательства). Тогда левую и правую части последнего тождества деля на 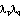, а затем дифференцируя результат по p и q, получаем

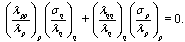
Предположим, что , значит 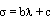, где b, c = const. Следовательно,решением уравнения (10) является МФ без свойства феноменологической симметрии. И, наконец, пусть 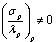, тогда разделяя переменные в последнем тождестве, получаем .
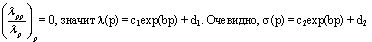Подставляя найденные функции в уравнение (10), после простых преобразований, приходим к тому, что МФ также не удовлетворяет свойству ФС. Пусти, наконец, в 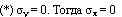, следовательно, МФ не является ФС. Таким образом, прямое утверждение теоремы доказано. Итак, теорема 1 доказана.

Теорема 2.Для того, чтобы непостоянная МФ (8), являющаяся решением уравнения (10) была феноменологически симметричной, необходимо и достаточно, чтобы

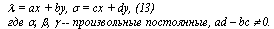
При доказательстве воспользуемся теоремой 1. Докажем сначала необходимость, для этого будем предполагать, что якобиан 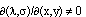. Дифференцируя тождество (12) по координатам точек i и j, приходим к системе функционально-дифференциальных уравнений:

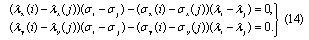
Продифференцируем каждое из тождеств системы (14) по всевозможным парам координат точек i и j

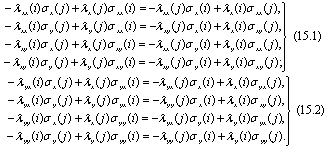
Проинтегрируем первые два уравнения систем (15.1) и (15.2) по x_i, а вторые по y_i, после чего фиксируя координаты точки j, после переобозначений, приходим

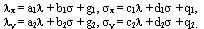
Подставляя найденные функции в систему тождеств (14), приходим к равенствам: a₁ = d₁, b₁ = c₁ = 0; a₂ = d₂, b₂ = c₂ = 0. В итоге получается система уравнений:

Тогда после интегрирования этой системы при 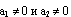, получаем

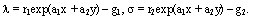
Подставляя найденные функции в уравнение (10), приходим

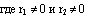, то есть решением является МФ без свойства ФС: 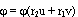или, что равносильно 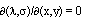, пришли к противоречию. Если, например, r1 = 0, то по лемме 3 также приходим к противоречию. Пусть в системе (16) a₁= 0. Тогда решая эту систему, получаем a₂ = 0,

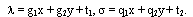
Накладывая на эту систему функций ограничение 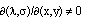, приходим к функциям (13). Таким образом, необходимость теоремы доказана. Достаточность утверждения теоремы очевидна. Теорема 2 доказана полностью.

Итак, нами доказано, что произвольный оператор (9) алгебры Ли группы движений геометрии с метрической функцией (8) представим в виде:

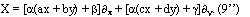
Справедлива классификационная теорема:

Теорема 3.Двухточечными инвариантами операторов (9') являются метрические функции (2) - (7) и только они.

Для доказательства теоремы необходимо проинтегрировать уравнение:

Для начала, выбором координат u и v, упростим уравнение (10''). Матрицу коэффициентов этого уравнения запишем в виде: . Рассмотрим линейную замену координат: 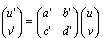. Тогда относительно новых координат матрицу уравнения (10'') можно записать в виде:. Выбором коэффициентов замены координат, приходим к таким представлениям уравнения (10''):

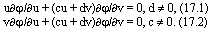
Проинтегрируем сначала уравнение (17.1). Если c = 0, то интегралом является функция , которая при d = 1 является МФ плоскости Минковского, при d = -1 --- МФ симплициальной плоскости, а в остальных случаях, кроме только d = 0 --- МФ псевдогельмгольцевой плоскости. Если c ? 0 и d = 1, то получим МФ дуальногельмгольцевой плоскости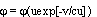. Пусть, наконец, 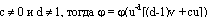, то есть возвращаемся к первому. Проинтегрируем теперь уравнение (17.2). Если d = 0, то интегралом является функция 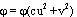, которая при c > 0 является МФ евклидовой плоскости, при c < 0 --- МФ псевдоевклидовой плоскости. Если 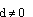, то при d₂ + 4c > 0 получим МФ псевдогельмгольцевой плоскости 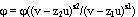; при d₂ + 4c = 0 --- МФ дуальногельмгольцевой плоскости 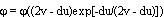, наконец, а при d2 + 4c < 0 --- МФ собственно гельмгольцевой плоскости
.
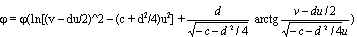Итак, теорема 3 доказана полностью.