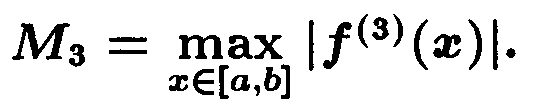Сплайн-интерполяция.

Определение 3.2 Сплайн (англ. spline - рейка, линейка) - это определенная в некоторой области G ∈ Rn кусочно-полиномиальная функция из класса Cr(G).

Таким образом в соответствии с определением существует разбиение области G на подобласти такое, что внутри каждой подобласти сплайн представляет собой полином некоторой степени М.

Определение 3.3 Интерполяция при помощи сплайнов называется сплайн-интерполяцией.

Рассмотрим одномерный случай (n=1) и наиболее употребительную кубическую сплайн-интерполяцию (M=3) из класса C2 (r=2).

Математическая постановка.

Пусть известные значения некоторой функции f(x) образуют таблицу 3.2 на отрезке [a,b], где a ≡ x0 < x1 < ... < xN ≡ b

x x0 x1 ... xN
f f0 f1 ... fN

Таблица 3.2: Табличная функция.

Требуется построить по данной таблице интерполяционный кубический сплайн из класса C2, то есть функцию g(x) со следующими свойствами:

1) g(x)C2 [a,b]

2) на любом отрезке [xi-1 , xi], i = 1, ..., N функция g(x) является полиномом третьей степени,

3) g(xi ) = fi , i = 0, ..., N.
Для однозначного решения этой задачи добавим следующее часто используемое условие:

4) g''(a)=g''(b)=0

ТЕОРЕМА 3.3 Функция, удовлетворяющая свойствам 1)-4), существует и единственна.

ДОКАЗАТЕЛЬСТВО Так как по свойству 1) функция g''(x) непрерывна на [a,b] и по свойству 2) линейна на каждом отрезке [xi-1 - x], i= 1, ...,N то можно записать x[xi-1,xi] следующее представление:

g''(x) = mi-1(xi - x)/hi + mi(x - xi-1 )/hi (3.7)

где hi=xi-xi-1 , mi=g''(xi). Проинтегрируем равенство (3.7) дважды. Получим:

g(x) = mi-1(xi - x)3/6hi + mi(x - xi-1 )3/6hi + Ai(xi - x)/hi + Bi(x - xi-1 )/hi (3.8)

где Ai, Bi - некоторые константы интегрирования. Найдем Ai и Bi, подставляя значения xi и xi-1 в (3.8):

fi = g(xi ) = mi hi2/6 + Bi , следовательно, Bi = fi - mi hi2/6

fi-1 = g(xi-1 ) = mi-1 hi2/6 + Ai , следовательно Ai = fi-1 - mi-1 hi2/6

Подставляя Ai и Bi в (3.8) получим равенство:

g(x) = mi-1(xi - x)3/6hi + mi(x - xi-1 )3/6hi + (fi-1 - mi-1 hi2/6)(xi - x)/hi + (fi - mi hi2/6)(x - xi-1 )/hi (3.9)

Тогда производная функции g(x) на [xi-1,xi] имеет вид:

g'(x) = -mi-1(xi - x)2/2hi + mi(x - xi-1 )2/2hi + mi-1 hi/6 - mi hi/6 + (fi - fi-1 )/hi (3.10)

Пользуясь формулой (3.10) найдем односторонние (слева и справа) пределы функции g'(x) в точках xi , i = 1, ..., N:

g'(xi - 0) = mi-1 hi /6 + mi hi /3 + (fi - fi-1 )/hi;
g'(xi + 0) = -mi hi+1 /3 - mi+1 hi+1 /6 + (fi+1 - fi )/hi+1

(последнее равенство получено из (3.10) заменой индекса i на i+1, то есть переходом на отрезок [xi,xi+1]). Так как по свойству 1) функция g'(x) непрерывна на отрезке [a,b], то приравнивая g'(xi+0) и g'(xi-0), i = 1, ..., N-1 получаем N-1 уравнение:

mi-1 hi /6 + mi (hi + hi+1 )/3 + mi+1 hi+1 /6 = (fi+1 - fi )/hi+1 - (fi - fi-1 )/hi , i = 1, ..., N-1 (3.11)

Учитывая, что по свойству 4) имеют место равенства

g''(x0)≡m0=0, g''(xN)≡mN=0 (3.12)

получаем линейную алгебраическую систему для нахождения неизвестных m1 , ..., mN-1:

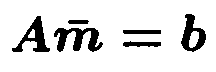(3.13)

где

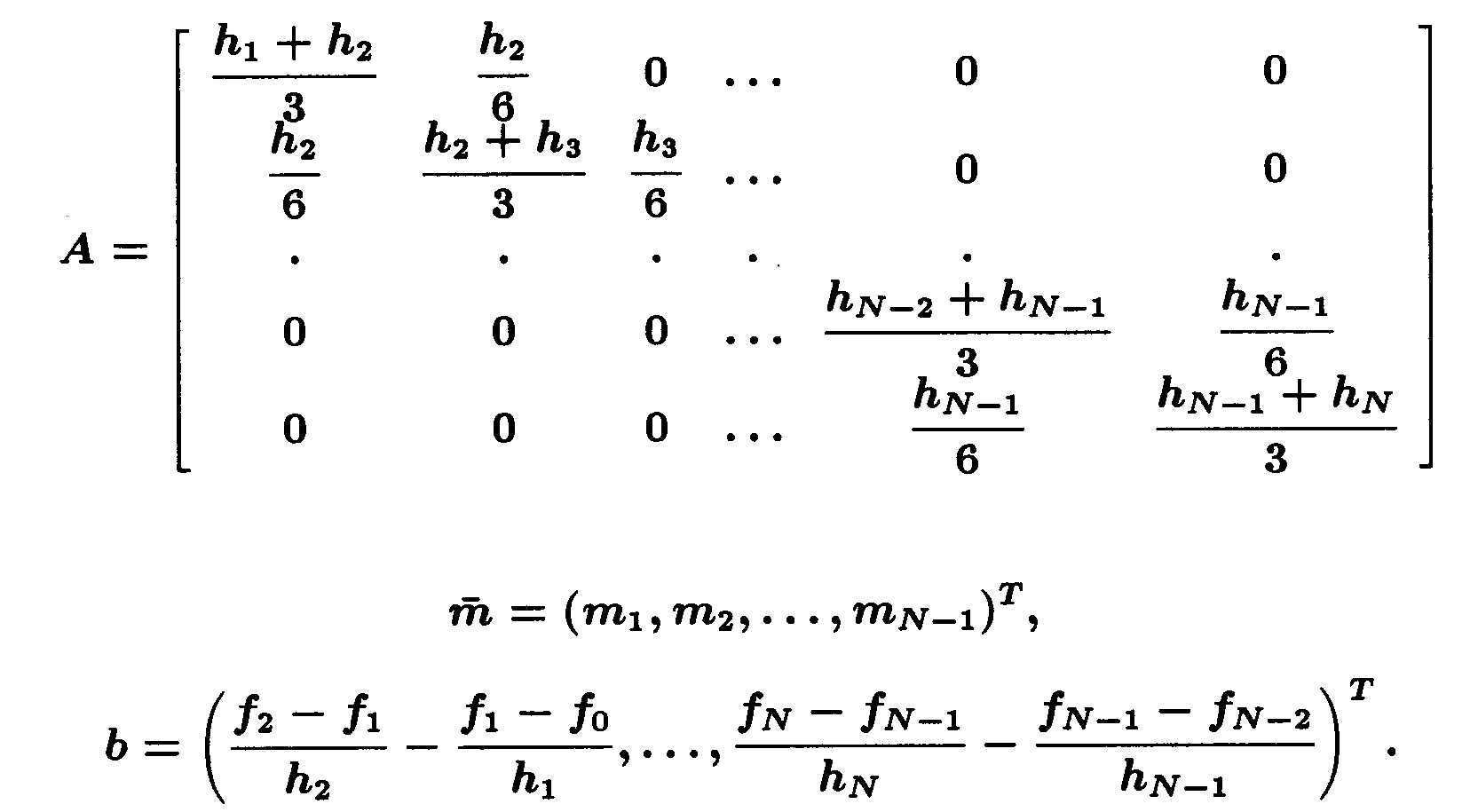
Очевидно, что матрица A имеет строгое диагональное преобладание. Но из курса алгебры известно, что такие матрицы невырождены.

Следовательно, система 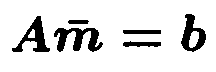однозначно разрешима относительно вектора , а тем самым функция со свойствами 1)-4) существует, единственна и представляется формулой (3.9).

ЗАМЕЧАНИЕ 3.7 На практике сплайн вычисляется на каждом отрезке [xi-1 , xi], i = 1, ..., N по формуле (3.9), с использованием табличной функции 3.2, равенств (3.12) и вектора 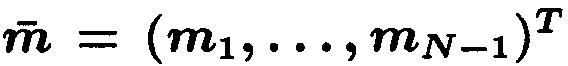, являющегося решением системы (3.13).

Оценку погрешности при сплайн-интерполяции дает следующее

УТВЕРЖДЕНИЕ 3.3 [3, стр.148] Если интерполируемая функция f(x) C 4[a,b], то для функции погрешности R(x)=f(x)-g(x) справедливо неравенство:

(3.14)

где

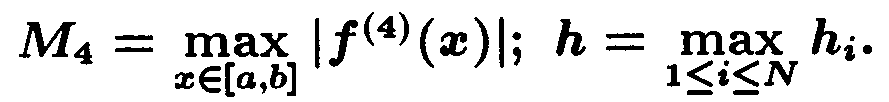
Меньше ограничений на функцию f(x) накладывает

УТВЕРЖДЕНИЕ 3.4 [11, стр.98] Если интерполируемая функция f(x)C 3[a,b] и разбиение отрезка [a,b] узлами интерполяции является равномерным (h=hi=const), то для функции погрешности R(x)=f(x)-g(x) справедливо неравенство:

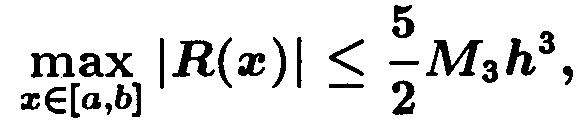(3.15)

где